Magnetism and Matter NotesMagnetism and Matter Book
[pdf id=’20918′]
Introduction ( Magnetism and matter )
Magnetism is the phenomenon due to which certain substances attract pieces of steel, iron, nickel etc.

Magnets are used in many devices like electric bell, telephone, radio, loud speaker, motors, fans, screw drivers, lifting heavy iron loads, super-fast trains especially in foreign coutries, refrigerators etc.
Magnetite is the world’s first magnet. This is also called natural maget. Though magnets occur naturally, we can also impart magnetic property on a substance. It would be an artificial magnet in that case.
History of magnets
- As early as 600 BC in Greece, shepherds observed that their wooden shoes which had iron nails struck at some places on the ground.

- An island in Greece called magnesia has magnetic ore deposits. The word magnet is derived from here.
- The technological use of magnet at around 400 BC by Chinese was remarkable. A thin piece of magnet when suspended freely always points towards North-South direction. This fact was utilised by a Chinese emperor Huang-ti to win a war.
Magnets – Known facts
- Earth behaves as a magnet
- When a bar magnet is freely suspended, it points to the NS direction

When two North poles are brought together, they repel each other. Similar effect is observed for South pole also

However, when a North pole and South pole is brought together, they attract each other

- Magnetic monopoles do not exists which means we cannot have a magnet with North pole alone or South pole alone
- If a bar magnet is broken in two halves, we get two similar bar magnets with weaker properties

- With the help of iron and its alloys, we can make magnets
Magnetic field lines
- When iron fillings are sprinkled on a sheet of glass placed over a short bar magnet, we observe a pattern. The pattern indicates that the magnet has two poles.
- This pictorially represents magnetic field lines. Thus, magnetic field lines are imaginary lines of magnetic field inside and around the magnet.

Some of the properties of the magnetic field lines are :
- The lines and continuous and outside the magnet, the field lines originate from the North pole and terminate at the South pole
- They form closed loops traversing inside the magnet. But here the lines seem to originate from the South pole and terminate at North pole to form closed loops.
- More number of close lines indicate stronger magnetic field
- The lines do not intersect each other
- The tangent drawn at the field line gives the direction of the field at that point.
Analogy – Circular Current loop and Current loop in uniform magnetic field
In chapter 1, Electric charges and fields, we studied about current carrying circular conductor.

he current carrying circular loop of N turns is analogous to magnetic dipole. In a current carrying loop, if we view from one side, say right side, the current appears to move in clockwise direction. This is like South polarity. If we view it from the other side, say left side, the current appears to move in the anticlockwise direction which is like North polarity.
Magnetic dipole moment of a current carrying loop is given by M = IA where
- Current – I
- Area of cross-section of the coil – A
For N such turns of the coil, Magnetic dipole moment M = NIA
The expression for moment in the case of current carrying loop having N turns is similar to rectangular loop placed in uniform magnetic field with area vector A. In both cases, m = NIA

Analogy – Solenoid and Bar magnet
Before the analogy, let is find out the magnetic field at a far axial point of a solenoid:
Let the consider the following
- Length of the solenoid – 2l
- Radius of the solenoid – r
- Number of turns / unit length – n
Also, consider,
- dx – a small element dx in the solenoid
- x – distance of dx from the centre of the solenoid
- r –distance of the point P from the centre of the solenoid O

As the magnetic field on the axis of a circular loop is

where R is the radius and x is the distance of the point from the centre of the circular loop




Expression for finding the value of magnetic field:
Take a compass with known value of magnetic moment m and moment of Intertia I . Allow the needle to oscillate in a magnetic field of value B.
The torque on the needle is given by


Expression for finding the value of magnetic potential energy :
In the above case, the magnetic potential energy (Um ) is the work done in taking the magnetic needle (NS) in the magnetic field B from the initial position to the final position.

umericals: A short bar magnet placed with its axis at 300 with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 4.5 * 10-2 What is the magnitude of magnetic moment of the magnet?
Given B = 0.25T, Ʈ = 4.5 * 10-2 J , Ɵ = 300 , M = ?
Ʈ = MB sinΘ
M = Ʈ / B sinΘ
= 4.5 * 10-2 / 0.25 * sin 30 = 0.36 J/T
Numericals: A short bar magnet of moment 0.32 JT-1 is placed in a uniform external magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its (a) stable (b) unstable equilibrium? What is the potential energy of the magnet in each case?
Given M = 0.32 JT-1
B = 0.15 T
- In stable equilibrium, the bar magnet would be aligned along the magnetic field and Ɵ = 00
P.E = – MBCosƟ = – 0.32 * 0.15 * cos 00 = -4.8 * 10-2 J
- In unstable equilibrium, the bar magnet would make and angle 180 0 with the magnetic field and Ɵ =1800
P.E = – MBCosƟ = – 0.32 * 0.15 * cos 1800 = 4.8 * 10-2 J
Numericals : A circular coil of 16 turns and radius 10cm carrying a current of 0.75 A rests with its plane normal to an external field of magnitude 5.0 * 10-2 When the coil is turned slightly and released, it oscillates about its stable equilibrium with frequency of 2.0 s-1 . What is the moment of inertia of the coil about its axis of rotation?
Given n = 16 turns
a = 10 * 10-2 m
I = .75 A
B=5.0 * 10-2 T
ט=2.0 s-1
I = ?
M = nIA = 16 * .75 * 3.14 * (10 * 10—2)2 = 0.377 J/T

= 0.377 * 5.0 * 10-2 / 4 * 3.14 * 3.14 * 2 * 2
= 1.2 * 10-4 kg m2
Numericals : A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is 600 and one of the field has a magnitude of 1.2 * 10-2T. If the dipole comes to a stable equilibrium at an angle of 150 with this field, what is the magnitude of the other field?
B1 = 1.2 * 10-2 T
B2 = ?
Angle between the two fields B1 and B2, Ɵ = 600
Angle between dipole and field B1, at stable equilibrium = Ɵ1 = 150
Angle between dipole and field B2,at stable equilibrium = Ɵ2 = Ɵ – Ɵ1
= 600 – 150 = 450
At rotational equilibrium, torque due to both fields should balance.
Hence,
Torque due to field B1 = Torque due to field B2
MB1 sin Ɵ1 = MB2 sin Ɵ2
B2 = B1 sin Ɵ1 / sin Ɵ2
= 1.2 * 10-2 * sin 15 / sin 45
= 4.39 * 10-3 T


Gauss law of magnetism in comparison with electrostatics
| Law | Electrostatics | Magnetism |
| Gauss | The flux through a closed surface is given by | The net magnetic flux through any closed surface is zero |
The above statement indicates that the same law in electrostatics extends to magnetism. In the case of magnetism, monopoles do not exist which means we cannot isolate N pole or S pole.
Hence, there is no accumulation of charge anywhere.
The number of lines entering an area is equal to the number of lines leaving the same area. Hence, net flux is zero.
Earth’s Magnetism
On the surface of the earth, the strength of the earth’s magnetic field varies from place to place and is of order 10-5 Testla.
Dynamo effect

Though there are many theories on earth’s magnetic field, dynamo effect seems to be most accepted one.
- The earth consists of core, mantle and crust
- In the outer core, there is molten iron and nickel
- The convective motion of these metallic fluids, results in electrical currents
- The magnetic field is due to this electrical currents
Magnetic lines of the earth
Let us imagine a magnetic dipole is present in the centre of the earth. Now, draw magnetic field lines. The magnetic lines of the earth resemble the same.


Magnetic poles :
The one small difference is the axis of the dipole does not coincide with the axis of rotation of earth and is tilted by approximately 11.30
Hence, apart from the geographic North Pole Ng and South Pole Sg, we also have magnetic North pole Nm and magnetic South Pole Sm.
Nomenclature of poles :
We know that in the case of a bar magnet, the magnetic lines go from the South Pole to the North Pole. So field lines come out from the North Pole.
However, in the case of the earth, the field lines go into the earth at the magnetic North pole and come out at the magnetic South pole.
When magnetic needle was suspended freely, the north pole of the needle coincided with the magnetic north pole. Hence, it became conventional to call it as North magnetic meridian, which is close to Geographic North pole.
Thus, in reality, the north magnetic pole behaves like South pole of bar magnet and vice versa.This is the reason why the needle having North pole is attached by the south pole behaviour of earth, though called as north magnetic pole.
Elements of earth’s magnetic field
The 3 elements of earth’s magnetic field are – (1) Angle of declination (α)
(2) Angle of dip (δ)and (3) Horizontal component of earth’s magnetic field (He)
To describe the magnetic field of earth at any point on the surface of the earth, we require the above 3 quantities.
Angle of declination (α) :
The angle between the geographical meridian and magnetic meridian is known as angle of declination.
This angle is smaller at the equator and greater at higher latitudes. At equator, the magnetic meridian will be close to geographic meridian.


Angle of dip / inclination (δ) :The angle made between the total of earth’s magnetic field (Be) with the surface of the earth (horizontal component) in the magnetic meridian is known as angle of dip.

The yellow lines indicate the surface of the earth. The blue lines indicate the total magnetic field of earth which is actually tangent to the magnetic field line. This angle of dip is 90 degrees at the equator and 0 degrees at the poles.
Horizontal component of earth’s magnetic field (He) :

The total magnetic field on the surface of the earth can be resolved into horizontal component He and vertical component Ze. The angle made by Be with He is the angle of dip δ
Hence,He = Be cos δ
Ve = Be sin δ
Ve / He = Be tan δ
Numericals: A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip pointing down at 220 with the horizontal. The horizontal component of earth’s magnetic field at the place is known to be 0.35 G.
Given H = 0.35G , δ = 220 , H = Be cos δ
Be = H / cos 22 = 0.35/ cos 22 = 0.38G
Terms used in Magnetism:- ( Magnetism and Matter )
Magnetization M : As we know, the nucleus of the atom consists of Neutrons and positively charged protons. The electrons which are negatively charged revolve around. Thus, the circulating electron in an atom has a magnetic moment.
In a material made of many atoms, these magnetic moments add up vectorially and give a net magnetic moment which is non-zero.
Hence, Magnetisation M = mnet / V which is net magnetic moment per unit volume. Its unit is A/m2
Magnetic Intensity / Magnetising force H:
Consider a solenoid of n turns per unit length and carrying a current I. Hence,
B0 = µ0 n I
The interior of the solenoid is filled with a material of non-zero magnetisation (M).

B = B0 + Bm
= B0 + µ0M
Dividing by µ0, B / µ0 = B0 /µ0 + M
B / µ0 = H + M [ H = B0 /µ0, the variation of magnetic field with permeability Is called Magnetic intensity ]
B = µ0 (H + M)
H depends on external factors like current flowing etc. Its unit is A/m2
M depends on the material inside the solenoid
Susceptibility χ :-
In the expression, B = µ0 (H + M)
M can also depend on external factors. Hence, M = χ H
where the χ dimensionless quantity is called Susceptibility It gives how a magnetic material responds to an external field. It is dimensionless quantity.
Permeability µ:-
B = µ0 (H + M)
B = µ0 (H + χH)
B = µ0 (1 + χ) H
=µ0µr H [ µ = µ0µr = µ0 (1 + χ)]
µ is called magnetic permeability of the substance. µr is relative magnetic permeability of the substance. Its unit is Tm/A.
Diamagnetic, Paramagnetic and Ferromagnetic substances:-
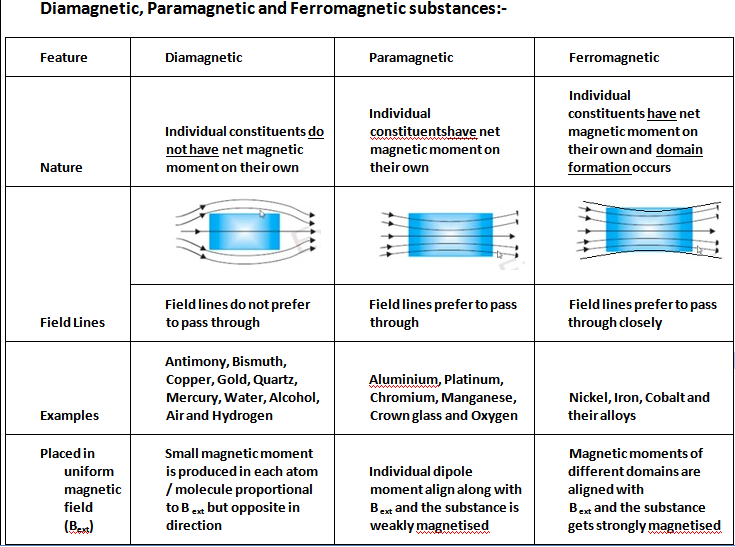




Key effects
Meissner’s effect :
- Superconductors are diamagnetic and hence repel and are also repelled by magnets
- When cooled to very low temperature, it exhibits perfect conductivity and diamagnetism
- This phenomenon is called Meissner effect
- Hence used in levitated superfast trains
Curie’s law :
- Magnetisation of paramagnetic substances is inversely proportional to absolute temperature
- M = C B0/T which is equivalent to
χ = C µ0 / T known as Curie’s law
Hence, the value of µ and ꭓ depends not only on the material but also on the temperature
- As field is increased or temperature is lowered (B /T), the magnetisation increases and reaches saturation Ms.
- Beyond this point Ms, Curie’s law is not obeyed
Curie Weiss’s law :
- The Curie–Weiss law describes the magnetic susceptibilityχ of a ferromagnet in the paramagnetic region above the Curie point
- At high temperature, Ferro magnet becomes paramagnet. The domain structure disintegrates with temperature
- This transition temperature is called Curie temperature Tc
- χ = C / ( T – Tc ) for temperature above Curie temperature
Types of Ferromagnets :-
Hard Ferro magnets – When external magnetic field is removed, magnetisation persists. These are called Hard ferromagnets Example – Alnico, Iodestone
Soft Ferro magnets – When external magnetic field is removed, magnetisation disappears. These are called Soft ferromagnets Example – Soft iron, Cobalt, Nickel, Gadolinium
Hysterisis
The word hysteresis means lagging behind. The phenomenon of lagging of intensity of magnetisation (M) behind magnetic intensity (H), when a specimen of magnetic material is subjected to a cycle of magnetization is called hysteresis.

The curve shown would very for different materials like steel, soft iron etc.
- Place an unmagnetised material inside the solenoid and increase the current through the solenoid. This increases the magnetic intensity (H) which is shown in X-axis
- As H increases, the magnetic field B in the material increases and reaches saturation as depicted in the graph as Oa.
- When saturation is reached, there is no point in increasing the current further
- Therefore, decrease the current. So H magnetic intensity also decreases.
- At a point when H is equal to zero, B in Y-axis is not equal to zero. This is indicated by ab.
- The value of H at B=0 is called retentivity or remanence.
- Next reverse the current and slowly increase the same. This is represented by bc. The value of H at c(B=0) is called coercivity
- As current increases, once again saturation is reached. Curve cd depicts this
- Then the current is reduced (de) and then reversed (curve ea)
- Note the curve ea is obtained and it does not trace the old path Oa

Permanent magnets and Electromagnets
| Feature | Permanent Magnet | Electromagnet |
| What is it? | Substances which retail ferromagnetic property for a long time at room temperature | In day to day applications, we need electro magnets which are again made of ferromagnetic materials Electric bells, loud speakers, Telephone Diaphragms, Cranes etc use electro magnets |
| Substances suitable | Steel, Alnico, Cobalt steel and ticonal | Soft Iron, Iron and Steel alloy |
| How can it be made? | · One of the method depicted in a 400 years old book is to hold an iron rod in NS direction and hammer it repeatedly · Hold a steel rod and stroke it with one end of a bar magnet many times always in the same direction · Place a ferro magnetic rod in a solenoid and pass current. The magnetic field of the solenoid magnetises the rod | Place a soft iron rod in a solenoid and pass current. Then switch off the solenoid current |
| Properties of the material | High retentivity – For the magnet to be strong High coercivity –Temperature fluctuation, minor mechanical action and stray magnetic fields nearby should not reduce the magnetic effect of the magnet High Permeability – so that it can be magnetised easily | High Permeability Low retentivity Narrow Hysteresis curve so that energy dissipated and heating should be small High resistivity – to lower losses due to eddy currents |