Download Magnetism and Matter notes , In this post We will Study, Magnetism and Matter Notes & Important Topic for Student to excel in exam. NCERT/CBSE class 12th Physics notes provided by free-education.in (Wisdom Education Academy). Here We are providing all subject wise pdf notes to student for their help to get good marks in exam.
In this post you can Download CBSE Physics PDF notes given below by free-education.in to excel in the exam.
www.free-education.in is a platform where you can get pdf notes from 6th to 12th class notes, General Knowledge post, Engineering post, Career Guidelines , English Speaking Trick , How to crack interview and lots more.
Introduction ( Magnetism and matter )
Magnetism is the phenomenon due to which certain substances attract pieces of steel, iron, nickel etc.

Magnets are used in many devices like electric bell, telephone, radio, loud speaker, motors, fans, screw drivers, lifting heavy iron loads, super-fast trains especially in foreign coutries, refrigerators etc.
Magnetite is the world’s first magnet. This is also called natural maget. Though magnets occur naturally, we can also impart magnetic property on a substance. It would be an artificial magnet in that case.
History of magnets
- As early as 600 BC in Greece, shepherds observed that their wooden shoes which had iron nails struck at some places on the ground.

- An island in Greece called magnesia has magnetic ore deposits. The word magnet is derived from here.
- The technological use of magnet at around 400 BC by Chinese was remarkable. A thin piece of magnet when suspended freely always points towards North-South direction. This fact was utilised by a Chinese emperor Huang-ti to win a war.
Magnets – Known facts
- Earth behaves as a magnet
- When a bar magnet is freely suspended, it points to the NS direction

When two North poles are brought together, they repel each other. Similar effect is observed for South pole also

However, when a North pole and South pole is brought together, they attract each other

- Magnetic monopoles do not exists which means we cannot have a magnet with North pole alone or South pole alone
- If a bar magnet is broken in two halves, we get two similar bar magnets with weaker properties

- With the help of iron and its alloys, we can make magnets
Magnetic field lines
- When iron fillings are sprinkled on a sheet of glass placed over a short bar magnet, we observe a pattern. The pattern indicates that the magnet has two poles.
- This pictorially represents magnetic field lines. Thus, magnetic field lines are imaginary lines of magnetic field inside and around the magnet.

Some of the properties of the magnetic field lines are :
- The lines and continuous and outside the magnet, the field lines originate from the North pole and terminate at the South pole
- They form closed loops traversing inside the magnet. But here the lines seem to originate from the South pole and terminate at North pole to form closed loops.
- More number of close lines indicate stronger magnetic field
- The lines do not intersect each other
- The tangent drawn at the field line gives the direction of the field at that point.
Analogy – Circular Current loop and Current loop in uniform magnetic field
In chapter 1, Electric charges and fields, we studied about current carrying circular conductor.

he current carrying circular loop of N turns is analogous to magnetic dipole. In a current carrying loop, if we view from one side, say right side, the current appears to move in clockwise direction. This is like South polarity. If we view it from the other side, say left side, the current appears to move in the anticlockwise direction which is like North polarity.
Magnetic dipole moment of a current carrying loop is given by M = IA where
- Current – I
- Area of cross-section of the coil – A
For N such turns of the coil, Magnetic dipole moment M = NIA
The expression for moment in the case of current carrying loop having N turns is similar to rectangular loop placed in uniform magnetic field with area vector A. In both cases, m = NIA

Analogy – Solenoid and Bar magnet
Before the analogy, let is find out the magnetic field at a far axial point of a solenoid:
Let the consider the following
- Length of the solenoid – 2l
- Radius of the solenoid – r
- Number of turns / unit length – n
Also, consider,
- dx – a small element dx in the solenoid
- x – distance of dx from the centre of the solenoid
- r –distance of the point P from the centre of the solenoid O

As the magnetic field on the axis of a circular loop is

where R is the radius and x is the distance of the point from the centre of the circular loop




Expression for finding the value of magnetic field:
Take a compass with known value of magnetic moment m and moment of Intertia I . Allow the needle to oscillate in a magnetic field of value B.
The torque on the needle is given by

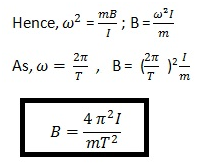
Expression for finding the value of magnetic potential energy :
In the above case, the magnetic potential energy (Um ) is the work done in taking the magnetic needle (NS) in the magnetic field B from the initial position to the final position.

umericals: A short bar magnet placed with its axis at 300 with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 4.5 * 10-2 What is the magnitude of magnetic moment of the magnet?
Given B = 0.25T, Ʈ = 4.5 * 10-2 J , Ɵ = 300 , M = ?
Ʈ = MB sinΘ
M = Ʈ / B sinΘ
= 4.5 * 10-2 / 0.25 * sin 30 = 0.36 J/T
Numericals: A short bar magnet of moment 0.32 JT-1 is placed in a uniform external magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its (a) stable (b) unstable equilibrium? What is the potential energy of the magnet in each case?
Given M = 0.32 JT-1
B = 0.15 T
- In stable equilibrium, the bar magnet would be aligned along the magnetic field and Ɵ = 00
P.E = – MBCosƟ = – 0.32 * 0.15 * cos 00 = -4.8 * 10-2 J
- In unstable equilibrium, the bar magnet would make and angle 180 0 with the magnetic field and Ɵ =1800
P.E = – MBCosƟ = – 0.32 * 0.15 * cos 1800 = 4.8 * 10-2 J
Numericals : A circular coil of 16 turns and radius 10cm carrying a current of 0.75 A rests with its plane normal to an external field of magnitude 5.0 * 10-2 When the coil is turned slightly and released, it oscillates about its stable equilibrium with frequency of 2.0 s-1 . What is the moment of inertia of the coil about its axis of rotation?
Given n = 16 turns
a = 10 * 10-2 m
I = .75 A
B=5.0 * 10-2 T
ט=2.0 s-1
I = ?
M = nIA = 16 * .75 * 3.14 * (10 * 10—2)2 = 0.377 J/T

= 0.377 * 5.0 * 10-2 / 4 * 3.14 * 3.14 * 2 * 2
= 1.2 * 10-4 kg m2
Numericals : A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is 600 and one of the field has a magnitude of 1.2 * 10-2T. If the dipole comes to a stable equilibrium at an angle of 150 with this field, what is the magnitude of the other field?
B1 = 1.2 * 10-2 T
B2 = ?
Angle between the two fields B1 and B2, Ɵ = 600
Angle between dipole and field B1, at stable equilibrium = Ɵ1 = 150
Angle between dipole and field B2,at stable equilibrium = Ɵ2 = Ɵ – Ɵ1
= 600 – 150 = 450
At rotational equilibrium, torque due to both fields should balance.
Hence,
Torque due to field B1 = Torque due to field B2
MB1 sin Ɵ1 = MB2 sin Ɵ2
B2 = B1 sin Ɵ1 / sin Ɵ2
= 1.2 * 10-2 * sin 15 / sin 45
= 4.39 * 10-3 T


Gauss law of magnetism in comparison with electrostatics
| Law | Electrostatics | Magnetism |
| Gauss | The flux through a closed surface is given by | The net magnetic flux through any closed surface is zero |
The above statement indicates that the same law in electrostatics extends to magnetism. In the case of magnetism, monopoles do not exist which means we cannot isolate N pole or S pole.
Hence, there is no accumulation of charge anywhere.
The number of lines entering an area is equal to the number of lines leaving the same area. Hence, net flux is zero.
Earth’s Magnetism
On the surface of the earth, the strength of the earth’s magnetic field varies from place to place and is of order 10-5 Testla.
Dynamo effect

Though there are many theories on earth’s magnetic field, dynamo effect seems to be most accepted one.
- The earth consists of core, mantle and crust
- In the outer core, there is molten iron and nickel
- The convective motion of these metallic fluids, results in electrical currents
- The magnetic field is due to this electrical currents
Magnetic lines of the earth
Let us imagine a magnetic dipole is present in the centre of the earth. Now, draw magnetic field lines. The magnetic lines of the earth resemble the same.


Magnetic poles :
The one small difference is the axis of the dipole does not coincide with the axis of rotation of earth and is tilted by approximately 11.30
Hence, apart from the geographic North Pole Ng and South Pole Sg, we also have magnetic North pole Nm and magnetic South Pole Sm.
Nomenclature of poles :
We know that in the case of a bar magnet, the magnetic lines go from the South Pole to the North Pole. So field lines come out from the North Pole.
However, in the case of the earth, the field lines go into the earth at the magnetic North pole and come out at the magnetic South pole.
When magnetic needle was suspended freely, the north pole of the needle coincided with the magnetic north pole. Hence, it became conventional to call it as North magnetic meridian, which is close to Geographic North pole.
Thus, in reality, the north magnetic pole behaves like South pole of bar magnet and vice versa.This is the reason why the needle having North pole is attached by the south pole behaviour of earth, though called as north magnetic pole.
Elements of earth’s magnetic field
The 3 elements of earth’s magnetic field are – (1) Angle of declination (α)
(2) Angle of dip (δ)and (3) Horizontal component of earth’s magnetic field (He)
To describe the magnetic field of earth at any point on the surface of the earth, we require the above 3 quantities.
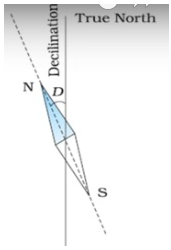
Angle of declination (α) :
The angle between the geographical meridian and magnetic meridian is known as angle of declination.
This angle is smaller at the equator and greater at higher latitudes. At equator, the magnetic meridian will be close to geographic meridian.

Angle of dip / inclination (δ) :The angle made between the total of earth’s magnetic field (Be) with the surface of the earth (horizontal component) in the magnetic meridian is known as angle of dip.

The yellow lines indicate the surface of the earth. The blue lines indicate the total magnetic field of earth which is actually tangent to the magnetic field line. This angle of dip is 90 degrees at the equator and 0 degrees at the poles.
Horizontal component of earth’s magnetic field (He) :

The total magnetic field on the surface of the earth can be resolved into horizontal component He and vertical component Ze. The angle made by Be with He is the angle of dip δ
Hence,He = Be cos δ
Ve = Be sin δ
Ve / He = Be tan δ
Numericals: A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip pointing down at 220 with the horizontal. The horizontal component of earth’s magnetic field at the place is known to be 0.35 G.
Given H = 0.35G , δ = 220 , H = Be cos δ
Be = H / cos 22 = 0.35/ cos 22 = 0.38G
Terms used in Magnetism:- ( Magnetism and Matter )
Magnetization M : As we know, the nucleus of the atom consists of Neutrons and positively charged protons. The electrons which are negatively charged revolve around. Thus, the circulating electron in an atom has a magnetic moment.
In a material made of many atoms, these magnetic moments add up vectorially and give a net magnetic moment which is non-zero.
Hence, Magnetisation M = mnet / V which is net magnetic moment per unit volume. Its unit is A/m2
Magnetic Intensity / Magnetising force H:
Consider a solenoid of n turns per unit length and carrying a current I. Hence,
B0 = µ0 n I
The interior of the solenoid is filled with a material of non-zero magnetisation (M).

B = B0 + Bm
= B0 + µ0M
Dividing by µ0, B / µ0 = B0 /µ0 + M
B / µ0 = H + M [ H = B0 /µ0, the variation of magnetic field with permeability Is called Magnetic intensity ]
B = µ0 (H + M)
H depends on external factors like current flowing etc. Its unit is A/m2
M depends on the material inside the solenoid
Susceptibility χ :-
In the expression, B = µ0 (H + M)
M can also depend on external factors. Hence, M = χ H
where the χ dimensionless quantity is called Susceptibility It gives how a magnetic material responds to an external field. It is dimensionless quantity.
Permeability µ:-
B = µ0 (H + M)
B = µ0 (H + χH)
B = µ0 (1 + χ) H
=µ0µr H [ µ = µ0µr = µ0 (1 + χ)]
µ is called magnetic permeability of the substance. µr is relative magnetic permeability of the substance. Its unit is Tm/A.
Diamagnetic, Paramagnetic and Ferromagnetic substances:-





Key effects
Meissner’s effect :
- Superconductors are diamagnetic and hence repel and are also repelled by magnets
- When cooled to very low temperature, it exhibits perfect conductivity and diamagnetism
- This phenomenon is called Meissner effect
- Hence used in levitated superfast trains
Curie’s law :
- Magnetisation of paramagnetic substances is inversely proportional to absolute temperature
- M = C B0/T which is equivalent to
χ = C µ0 / T known as Curie’s law
Hence, the value of µ and ꭓ depends not only on the material but also on the temperature
- As field is increased or temperature is lowered (B /T), the magnetisation increases and reaches saturation Ms.
- Beyond this point Ms, Curie’s law is not obeyed
Curie Weiss’s law :
- The Curie–Weiss law describes the magnetic susceptibilityχ of a ferromagnet in the paramagnetic region above the Curie point
- At high temperature, Ferro magnet becomes paramagnet. The domain structure disintegrates with temperature
- This transition temperature is called Curie temperature Tc
- χ = C / ( T – Tc ) for temperature above Curie temperature
Types of Ferromagnets :-
Hard Ferro magnets – When external magnetic field is removed, magnetisation persists. These are called Hard ferromagnets Example – Alnico, Iodestone
Soft Ferro magnets – When external magnetic field is removed, magnetisation disappears. These are called Soft ferromagnets Example – Soft iron, Cobalt, Nickel, Gadolinium
Hysterisis
The word hysteresis means lagging behind. The phenomenon of lagging of intensity of magnetisation (M) behind magnetic intensity (H), when a specimen of magnetic material is subjected to a cycle of magnetization is called hysteresis.

The curve shown would very for different materials like steel, soft iron etc.
- Place an unmagnetised material inside the solenoid and increase the current through the solenoid. This increases the magnetic intensity (H) which is shown in X-axis
- As H increases, the magnetic field B in the material increases and reaches saturation as depicted in the graph as Oa.
- When saturation is reached, there is no point in increasing the current further
- Therefore, decrease the current. So H magnetic intensity also decreases.
- At a point when H is equal to zero, B in Y-axis is not equal to zero. This is indicated by ab.
- The value of H at B=0 is called retentivity or remanence.
- Next reverse the current and slowly increase the same. This is represented by bc. The value of H at c(B=0) is called coercivity
- As current increases, once again saturation is reached. Curve cd depicts this
- Then the current is reduced (de) and then reversed (curve ea)
- Note the curve ea is obtained and it does not trace the old path Oa

Permanent magnets and Electromagnets
| Feature | Permanent Magnet | Electromagnet |
| What is it? | Substances which retail ferromagnetic property for a long time at room temperature | In day to day applications, we need electro magnets which are again made of ferromagnetic materials Electric bells, loud speakers, Telephone Diaphragms, Cranes etc use electro magnets |
| Substances suitable | Steel, Alnico, Cobalt steel and ticonal | Soft Iron, Iron and Steel alloy |
| How can it be made? | · One of the method depicted in a 400 years old book is to hold an iron rod in NS direction and hammer it repeatedly · Hold a steel rod and stroke it with one end of a bar magnet many times always in the same direction · Place a ferro magnetic rod in a solenoid and pass current. The magnetic field of the solenoid magnetises the rod | Place a soft iron rod in a solenoid and pass current. Then switch off the solenoid current |
| Properties of the material | High retentivity – For the magnet to be strong High coercivity –Temperature fluctuation, minor mechanical action and stray magnetic fields nearby should not reduce the magnetic effect of the magnet High Permeability – so that it can be magnetised easily | High Permeability Low retentivity Narrow Hysteresis curve so that energy dissipated and heating should be small High resistivity – to lower losses due to eddy currents |
Download pdf notes for Physics Chapter 5 Magnetism and Matter
CBSE Class 12 Physics Important Questions Chapter 5 – Magnetism And Matter
1 Mark Questions
1. How does the intensity of magnetization of a paramagnetic material vary with increasing applied magnetic field?
Ans. Intensity of magnetization increases with the increase in applied magnetic field.
2. An iron bar magnet is heated to and then cooled in a magnetic field free space. Will it retain magnetism?
Ans. Curie temperature of iron is about but when it is heated to a very higher temperature magnetism of iron further gets lost and it will not retain
magnetism.
3. How will the magnetic field intensity at the centre of a circular wire carrying current change, if the current through the wire is doubled and radius of the coil is halved?
Ans. Since B =
B’= 4B
4. Can neutrons be accelerated in a cyclotron? Why?
Ans. No, neutrons cannot be accelerated in a cyclotron because neutron is neutral and cyclotron can accelerate only charged particles.
5. What type of magnetic material is used in making permanent magnets?
Ans.Material having high coercivity is used in making permanent magnets.
6. Which physical quantity has the unit? Is it a scalar or a vector quantity?
Ans. Magnetic field. It is a vector quantity.
2 Marks Questions
1. A bar magnet of magnetic moment M is aligned parallel to the direction of a uniform magnetic field B. What is the work done to turn the magnet, so as the align its magnetic moment?
(i) Opposite to the field direction
(ii) Normal to the field direction?
Ans. Since work done W = MB
(i)
W = MB [1- (-1)]
W = 2MB
(ii)
W = MB
W = MB
2. An electron in the ground state of hydrogen atom is revolving in anti – clock wise direction in a circular orbit. The atom is placed normal to the electron orbit makes an angle of 30o in the magnetic field. Find the torque experienced by the orbiting electron?
Ans. Magnetic moment associated with electron M =
3. Define angle of dip. Deduce the relation connecting angle of dip and horizontal component of earth’s total magnetic field with the horizontal direction.
Ans.
4. A point change +q is moving with speed perpendicular to the magnetic field B as shown in the figure. What should be the magnitude and direction of the applied electric field so that the net force acting on the charge is zero?
Ans. Force on the charge due to magnetic field = qVB sin
Since to the plane of paper and in words
F = qVB
F = qVB (along OY)
Force on the charge due to electric field
F = qE
Net force on change is zero if qE = qVB
E = VB
(along YO)
5. The energy of a charged particle moving in a uniform magnetic field does not change. Why?
Ans. The force on a charged particle in a uniform magnetic field always acts in a direction perpendicular to the motion of the charge. Since work done by the magnetic field on the charge is zero, hence energy of the charged particle will not change.
6. In the figure, straight wire AB is fixed; white the loop is free to move under the influence of the electric currents flowing in them. In which direction does the loop begin to move? Justify.
Ans. Since current in AB and arm PQ are in same direction therefore wire will attract the arm PQ with a force (say)
But repels the arm RS with a force (say)
Sine arm PQ is closer to the wire AB
i.e. the loop will move towards the wire.
7. State two factors by which voltage sensitivity of a moving coil galvanometer can be increased?
Ans. Voltage sensitivity =
It can be increased by
(1) increasing B using powerful magnets
(2) decreasing k by using phosphor borne strip
8. What is the magnetic moment associated with a coil of 1 turns, area of cross- section carrying a current of 2A?
Ans. m = NIA
9. A Rowland ring of mean radius 15 cm has 3500 turns of wire wound on a ferromagnetic core of relative permeability 800. What is the magnetic field B in the core for a magnetising current of 1.2 A?
Ans. Mean radius of a Rowland ring, r= 15 cm = 0.15 m
Number of turns on a ferromagnetic core, N= 3500
Relative permeability of the core material,
Magnetising current, I= 1.2 A
The magnetic field is given by the relation:
B
Where,
= Permeability of free space =
Therefore, the magnetic field is n the core is 4.48 T.
10. At a certain location in Africa, a compass points west of the geographic north. The north tip of the magnetic needle of a dip circle placed in the plane of magnetic meridian points above the horizontal. The horizontal component of the earth’s field is measured to be 0.16 G. Specify the direction and magnitude of the earth’s field at the location.
Ans. Angle of declination,
Angle of dip,
Horizontal component of earth’s magnetic field, BH= 0.16 G
Earth’s magnetic field at the given location = B
We can relate B and BH as:
Earth’s magnetic field lies in the vertical plane, West of the geographic meridian, making an angle of 60°(upward) with the horizontal direction. Its magnitude is 0.32ss G.
11. A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip pointing down at with the horizontal. The horizontal component of the earth’s magnetic field at the place is known to be 0.35 G. Determine the magnitude of the earth’s magnetic field at the place.
Ans. Horizontal component of earth’s magnetic field, BH= 0.35 G
Angle made by the needle with the horizontal plane = Angle of dip =
Earth’s magnetic field strength = B
We can relate B and BH as:
Hence, the strength of earth’s magnetic field at the given location is 0.377 G.
12. If the solenoid in Exercise 5.5 is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25 T is applied, what is the magnitude of torque on the solenoid when its axis makes an angle of with the direction of applied field?
Ans. Magnetic field strength, B = 0.25 T
Magnetic moment, M=
The angle, between the axis of the solenoid and the direction of the applied field is
Therefore, the torque acting on the solenoid is given as:
13. A closely wound solenoid of 800 turns and area of cross section carries a current of 3.0 A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment?
Ans. Number of turns in the solenoid, n = 800
Area of cross-section, A=
Current in the solenoid, I= 3.0 A
A current-carrying solenoid behaves as a bar magnet because a magnetic field develops along its axis, i.e., along its length.
The magnetic moment associated with the given current-carrying solenoid is calculated as:
M= n I A
=
=
14. A short bar magnet placed with its axis at with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to. What is the magnitude of magnetic moment of the magnet?
Ans. Magnetic field strength, B= 0.25 T
Torque on the bar magnet, T=
Angle between the bar magnet and the external magnetic field,
Torque is related to magnetic moment (M) as:
T= MB sin θ
Hence, the magnetic moment of the magnet is .
3 Marks Questions
1. A short bar magnet of magnetic moment 0.9 J/T is placed with its axis at 60o to a uniform magnetic field. It experiences a torque of 0.063 Nm. (i) calculate the strength of the magnetic field and (ii) what orientation of the bar magnet corresponds to the equilibrium position in the magnetic field?
Ans. (i) Since
Here
(ii) The magnet will be in stable equilibrium in the magnetic field if
i.e When magnet aligns itself parallel to the field
2. A beam of electrons is moving with a velocity of and carries a current of 1A.
(a) How many electrons per second pass a given point?
(b) How many electrons are in 1m of the beam?
(c) What is the total force on all the electrons in 1m of the beam if it passes through the field of ?
Ans.
(a)
(b) Electrons traverse a distance of in 1 s
No. of electrons in 1 meter of the beam
(c) Force on 1 meter of the beam of electrons
3. What is the main function of soft iron core used in a moving coil galvanometer? A galvanometer gives full deflection for Ig. Can it be converted into an ammeter of range I < Ig?
Ans. Soft iron core is used the moving coil galvanometer because it increases the strength of the magnetic field thus increases the sensitivity of the galvanometer.
We know S =
For I < Ig, S becomes negative
Hence it cannot be converted into an ammeter of range I < Ig.
4. Two wires loops PQRSP formed by joining two semicircular wires of radii carries a current I as shown in the figure. What is the direction of the magnetic induction at the centre C.?
Ans. Magnetic field due to semicircle QR at C. is
Magnetic field due to semicircle is at C is
Net field
5. A circular coil is placed in uniform magnetic field of strength 0.10T normal to the plane of coil. If current in the coil is 5.0A. Find.
(a) Total torque on the coil
(b) Total force on the coil
(c) Average force on each electron due to magnetic field
(The coil is made of copper wire of cross- sectional area and free electron density in copper is)
Ans. (a) B = 0.10T
(Normal to plane of the coil)
I = 5.0 A, Area = n =
(b) Total force on the coil = 0 Newton
(c) Fav = q )
(I = neAVd)
Fav =
Fav =
6. Using Ampere’s circuital law, derive an expression for magnetic field along the axis of a Toroidal solenoid?
Ans. If n be the no, of turns per unit length I be the current flowing through the Toroid
Then from Ampere’s circuital law
7. A short bar magnet of magnetic moment m = is placed in a uniform magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its (a) stable, and (b) unstable equilibrium? What is the potential energy of the magnet in each case?
Ans. Moment of the bar magnet, M=
External magnetic field, B= 0.15 T
(a) The bar magnet is aligned along the magnetic field. This system is considered as being in stable equilibrium. Hence, the angle, between the bar magnet and the magnetic field is.
Potential energy of the system
(b) The bar magnet is oriented 180°to the magnetic field. Hence, it is in unstable equilibrium.
Potential energy = – MB
8. A closely wound solenoid of 2000 turns and area of cross-section, carrying a current of 4.0 A, is suspended through its centre allowing it to turn in a horizontal plane.
(a) What is the magnetic moment associated with the solenoid?
(b) What is the force and torque on the solenoid if a uniform horizontal magnetic field of is set up at an angle of with the axis of the solenoid?
Ans. Number of turns on the solenoid, n = 2000
Area of cross-section of the solenoid, A=
Current in the solenoid, I= 4 A
(a) The magnetic moment along the axis of the solenoid is calculated as:
M= nAI
=
= 1.28 A
(b) Magnetic field, B =
Angle between the magnetic field and the axis of the solenoid,
Torque,
Since the magnetic field is uniform, the force on the solenoid is zero. The torque on the solenoid is s
9. A circular coil of 16 turns and radius 10 cm carrying a current of 0.75 A rests with its plane normal to an external field of magnitude . The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillates about its stable equilibrium with a frequency of . What is the moment of inertia of the coil about its axis of rotation?
Ans.Number of turns in the circular coil, N= 16
Radius of the coil, r= 10 cm = 0.1 m
Cross-section of the coil, A=
Current in the coil, I= 0.75 A
Magnetic field strength, B=
Frequency of oscillations of the coil, v=
∴Magnetic moment, M= NIA
=
=
Frequency is given by the relation:
Where,
I= Moment of inertia of the coil
Hence, the moment of inertia of the coil about its axis of rotation is
10. A short bar magnet has a magnetic moment of . Give the direction and magnitude of the magnetic field produced by the magnet at a distance of 10 cm from the centre of the magnet on (a) the axis, (b) the equatorial lines (normal bisector) of the magnet.
Ans. Magnetic moment of the bar magnet, M=
(a) Distance, d = 10 cm = 0.1 m
The magnetic field at distance d, from the centre of the magnet on the axis is given by the relation:
ss
Where,
= Permeability of free space =
The magnetic field is along the S – N direction.
(b) The magnetic field at a distance of 10 cm (i.e., d= 0.1 m) on the equatorial line of the magnet is given as:
The magnetic field is along the N – S direction.
11. A short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north-south direction. Null points are found on the axis of the magnet at 14 cm from the centre of the magnet. The earth’s magnetic field at the place is 0.36 G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null-point (i.e., 14 cm) from the centre of the magnet? (At null points, field due to a magnet is equal and opposite to the horizontal component of earth’s magnetic field.)
Ans. Earth’s magnetic field at the given place, H= 0.36 G
The magnetic field at a distance d, on the axis of the magnet is given as:
……(i)
Where,
= Permeability of free space
M= Magnetic moment
The magnetic field at the same distance d, on the equatorial line of the magnet is given as:
[Using equation (i)]
Total magnetic field,
Hence, the magnetic field is 0.54 G in the direction of earth’s magnetic field.
12. A long straight horizontal cable carries a current of 2.5 A in the direction south of west to 10°north of east. The magnetic meridian of the place happens to be west of the geographic meridian. The earth’s magnetic field at the location is 0.33 G, and the angle of dip is zero. Locate the line of neutral points (ignore the thickness of the cable). (At neutral points, magnetic field due to a current-carrying cable is equal and opposite to the horizontal component of earth’s magnetic field.)
Ans. Current in the wire, I= 2.5 A
Angle of dip at the given location on earth,
Earth’s magnetic field, H= 0.33 G =
The horizontal component of earth’s magnetic field is given as:
= H cos
The magnetic field at the neutral point at a distance Rfrom the cable is given by the relation:
Where,
= Permeability of free space =
Hence, a set of neutral points parallel to and above the cable are located at a normal distance of 1.51 cm.
13. A compass needle free to turn in a horizontal plane is placed at the centre of circular coil of 30 turns and radius 12 cm. The coil is in a vertical plane making an angle of with the magnetic meridian. When the current in the coil is 0.35 A, the needle points west to east.
(a) Determine the horizontal component of the earth’s magnetic field at the location.
(b) The current in the coil is reversed, and the coil is rotated about its vertical axis by an angle of 90º in the anticlockwise sense looking from above. Predict the direction of the needle. Take the magnetic declination at the places to be zero.
Ans. Number of turns in the circular coil, N= 30
Radius of the circular coil, r= 12 cm = 0.12 m
Current in the coil, I= 0.35 A
Angle of dip,
(a) The magnetic field due to current I, at a distance r, is given as:
s
Where,
= Permeability of free space =
s
=
The compass needle points from West to East. Hence, the horizontal component of earth’s magnetic field is given as:
=
(b) When the current in the coil is reversed and the coil is rotated about its vertical axis by an angle of, the needle will reverse its original direction. In this case, the needle will point from East to West.
14. A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is, and one of the fields has a magnitude of If the dipole comes to stable equilibrium at an angle of with this field, what is the magnitude of the other field?
Ans. Magnitude of one of the magnetic fields
Magnitude of the other magnetic field =
Angle between the two fields,
At stable equilibrium, the angle between the dipole and field
Angle between the dipole and field =
At rotational equilibrium, the torques between both the fields must balance each other.
∴ Torque due to field
Where,
M= Magnetic moment of the dipole
s
Hence, the magnitude of the other magnetic field is
15. The magnetic moment vectors and associated with the intrinsic spin angular momentum S and orbital angular momentum l, respectively, of an electron are predicted by quantum theory (and verified experimentally to a high accuracy) to be given by:
, Which of these relations is in accordance with the result expected classically? Outline the derivation of the classical result.
Ans. The magnetic moment associated with the orbital angular momentum is valid with the classical mechanics.
The magnetic moment associated with the orbital angular (l) momentum is given as
For current i and area of cross-section A, we have the relation:
Magnetic moment
Where,
e = Charge of the electron
r = Radius of the circular orbit
T = Time taken to complete one rotation around the circular orbit of radius r
Angular momentum,
Where,
M = Mass of the electron
V = Velocity of the electorn
Dividing equation (1) by equation (2),we get:
Therefore of the two relations, is in accordance with class physics.
5 Marks Questions
1. A particle of mass m and charge q moving with a uniform speed normal to a uniform magnetic field B describes a circular path of radius & Derive expressions for (1) Radius of the circular path (2) time period of revolution (3) Kinetic energy of the particle?
Ans. A particle of mass (m) and change (q) moving with velocity normal to describes a circular path if
Since Time period of Revolution
During circular path =
=> ()
=> T =
Kinetic energy K.E =
=> KE =
2. Write an expression for the force experienced by the charged particle moving in a uniform magnetic field B With the help of labeled diagram explain the working of cyclotron? Show that cyclotron frequency does not depend upon the speed of the particle?
Ans. Force experienced by the charged particle moving at right angles to uniform magnetic field with velocity is given by = q () Initially Dee is negatively charged and Dee is positively charged so, the positive ion will get accelerated towards Dee since the magnetic field is uniform and acting at right angles to the plane of the Dees so the ion completes a circular path in when ions comes out into the gap, polarity of the Dee’s gets reversed used the ion is further accelerated towards Dee with greater speed and cover a bigger semicircular path. This process is separated time and again and the speed of the ion becomes faster till it reaches the periphery of the dees where it is brought out by means of a deflecting plate and is made to bombard the target.
Since F = qVBsin900 provides the necessary centripetal force to the ion to cover a circular path so we can say
=> r =
Time period =
V =
frequency is independent of velocity
3. (a) Obtain an expression for the torque acting on a current carrying circular loop.
(b) What is the maximum torque on a galvanometer coil 5 cm 12 cm of 600 turns when carrying a current of 10-5 A. in a field where flux density is?
Ans. ABCD is a rectangular loop of length (L), breadth (b) and area (A). Let I be the Current flowing in the anti clockwise direction. Let be the angle between the normal to the loop and magnetic field
Force acting on arm AB of the loop
Force on arm CD
Force on arm BC
Force on arm DA
Since are equal and opposite and also acts along the same line, hence they cancel each other.
are also equal and opposite but their line of action is different, so they form a couple and makes the rectangular loop rotate anti clockwise.
Thus = either force distance
For loop of N turns
Where M is magnetic moment of the loop.
Torque will be maximum when = 90o
4. The current sensitivity of a moving coil galvanometer increases by 20% when its resistance is increased by a factor of two. Calculate by what factor, the voltage sensitivity changes?
Ans. Current sensitivity
Voltage sensitivity
Resistance of a galvanometer increases when n and A are changed
Given = 2R
Then n = and A =
New current sensitivity
New voltage sensitivity
From (i) and (iii)
n’A’=
Using equation (iv)
Thus voltage sensitivity decreases by a factor of .
5. (a) Show how a moving coil galvanometer can be converted into an ammeter?
(b) A galvanometer has a resistance 30 and gives a full scale deflection for a current of 2mA. How much resistance in what way must be connected to convert into?
(1) An ammeter of range 0.3A
(2) A voltammeter of range 0.2V.
Ans. (a) A galvanometer can be converted into an ammeter by connecting a low resistance called shunt parallel to the galvanometer.
Since G and RS are in parallel voltage across then is same
(b) (1) I = 0.3A G = 30 Ig = 2mA =
Sheent (S) =
S = 0.2
(2) G = 30, Ig = 2mA =, V = 0.2V
Shunt Resistance (R)
R = 70
6. A monoenergetic (18 keV) electron beam initially in the horizontal direction is subjected to a horizontal magnetic field of 0.04 G normal to the initial direction. Estimate the up or down deflection of the beam over a distance of 30 cm (me=). [Note: Data in this exercise are so chosen that the answer will give you an idea of the effect of earth’s magnetic field on the motion of the electron beam from the electron gun to the screen in a TV set.]
Ans. Energy of an electron beam, E= 18 keV =
Charge on an electron, e=
E=
Magnetic field, B = 0.04 G
Mass of an electron, me=
Distance up to which the electron beam travels, d = 30 cm = 0.3 m
We can write the kinetic energy of the electron beam as:
The electron beam deflects along a circular path of radius, r.
The force due to the magnetic field balances the centripetal force of the path.
Let the up and down deflection of the electron beam be
Where,
θ= Angle of declination
Therefore, the up and down deflection of the beam is 3.9 mm.
7. A sample of paramagnetic salt contains atomic dipoles each of dipole moment . The sample is placed under a homogeneous magnetic field of 0.64 T, and cooled to a temperature of 4.2 K. The degree of magnetic saturation achieved is equal to 15%. What is the total dipole moment of the sample for a magnetic field of 0.98 T and a temperature of 2.8 K? (Assume Curie’s law)
Ans. Number of atomic dipoles, n=
Dipole moment of each atomic dipole, M=
When the magnetic field, = 0.64 T
The sample is cooled to a temperature, = 4.2°K
Total dipole moment of the atomic dipole,
=
=
Magnetic saturation is achieved at 15%.
Hence, effective dipole moment,
When the magnetic field, = 0.98 T
Temperature, = 2.8°K
Its total dipole moment =
According to Curie’s law, we have the ratio of two magnetic dipoles as:
Therefore, is the total dipole moment of the sample for a magnetic field of 0.98 T and a temperature of 2.8 K.
8. A telephone cable at a place has four long straight horizontal wires carrying a current of 1.0 A in the same direction east to west. The earth’s magnetic field at the place is 0.39 G, and the angle of dip is. The magnetic declination is nearly zero. What are the resultant magnetic fields at points 4.0 cm below the cable?
Ans. Number of horizontal wires in the telephone cable, n= 4
Current in each wire, = 1.0 A
Earth’s magnetic field at a location, H= 0.39 G =
Angle of dip at the location,
Angle of declination,
For a point 4 cm below the cable:
Distance, r = 4 cm = 0.04 m
The horizontal component of earth’s magnetic field can be written as:
Where,
B= Magnetic field at 4 cm due to current I in the four wires
= Permeability of free space =
= 0 = 0.2 G
∴
=
The vertical component of earth’s magnetic field is given as:
Hv= Hsin
The angle made by the field with its horizontal component is given as:
The resultant field at the point is given as:
s
For a point 4 cm above the cable:
Horizontal component of earth’s magnetic field:
= 0.39 cos 35° + 0.2 = 0.52 G
Vertical component of earth’s magnetic field:
= 0.39
Angle,
And resultant field:
9. Answer the following questions:
(a) Explain qualitatively on the basis of domain picture the irreversibility in the magnetisation curve of a ferromagnet.
(b) The hysteresis loop of a soft iron piece has a much smaller area than that of a carbon steel piece. If the material is to go through repeated cycles of magnetisation, which piece will dissipate greater heat energy?
(c) ‘A system displaying a hysteresis loop such as a ferromagnet, is a device for storing memory?’ Explain the meaning of this statement.
(d) What kind of ferromagnetic material is used for coating magnetic tapes in a cassette player, or for building ‘memory stores’ in a modern computer?
(e) A certain region of space is to be shielded from magnetic fields.
Suggest a method.
Ans. The hysteresis curve (B–H curve) of a ferromagnetic material is shown in the following figure.
(a) It can be observed from the given curve that magnetisation persists even when the external field is removed. This reflects the irreversibility of a ferromagnet.
(b) The dissipated heat energy is directly proportional to the area of a hysteresis loop. A carbon steel piece has a greater hysteresis curve area. Hence, it dissipates greater heat energy.
(c) The value of magnetisation is memory or record of hysteresis loop cycles of magnetisation. These bits of information correspond to the cycle of magnetisation. Hysteresis loops can be used for storing information.
(d) Ceramic is used for coating magnetic tapes in cassette players and for building memory stores in modern computers.
(e) A certain region of space can be shielded from magnetic fields if it is surrounded by soft iron rings. In such arrangements, the magnetic lines are drawn out of the region.
10. Answer the following questions:
(a) Why does a paramagnetic sample display greater magnetisation (for the same magnetising field) when cooled?
(b) Why is diamagnetism, in contrast, almost independent of temperature?
(c) If a to roid uses bismuth for its core, will the field in the core be (slightly) greater or (slightly) less than when the core is empty?
(d) Is the permeability of a ferromagnetic material independent of the magnetic field? If not, is it more for lower or higher fields?
(e) Magnetic field lines are always nearly normal to the surface of a ferromagnetic at every point. (This fact is analogous to the static electric field lines being normal to the surface of a conductor at every point.) Why?
(f) Would the maximum possible magnetisation of a paramagnetic sample be of the same order of magnitude as the magnetization of a ferromagnet?
Ans. (a)Owing to therandom thermal motion of molecules, the alignments of dipoles get disrupted at high temperatures. On cooling, this disruption is reduced. Hence, a paramagnetic sample displays greater magnetisation when cooled.
(b) The induced dipole moment in a diamagnetic substance is always opposite to the magnetising field. Hence, the internal motion of the atoms (which is related to the temperature) does not affect the diamagnetism of a material.
(c) Bismuth is a diamagnetic substance. Hence, a toroid with a bismuth core has a magnetic field slightly greater than a toroid whose core is empty.
(d) The permeability of ferromagnetic materials is not independent of the applied magnetic field. It is greater for a lower field and vice versa.
(e) The permeability of a ferromagnetic material is not less than one. It is always greater than one. Hence, magnetic field lines are always nearly normal to the surface of such materials at every point.
(f) The maximum possible magnetisation of a paramagnetic sample can be of the same order of magnitude as the magnetisation of a ferromagnet. This requires high magnetising fields for saturation.
11. A short bar magnet of magnetic moment is placed with its axis perpendicular to the earth’s field direction. At what distance from the centre of the magnet, the resultant field is inclined at 45º with earth’s field on s
(a) its normal bisector and (b) its axis. Magnitude of the earth’s field at the place is given to be 0.42 G. Ignore the length of the magnet in comparison to the distances involved.
Ans. Magnetic moment of the bar magnet, M=
Magnitude of earth’s magnetic field at a place, H= 0.42 G =
(a) The magnetic field at a distance R from the centre of the magnet on the normal bisector is given by the relation:
Where,
= Permeability of free space =
When the resultant field is inclined at with earth’s field, B= H
(b) The magnetic field at a distanced from the centre of the magnet on its axis is given as:
The resultant field is inclined at with earth’s field.
12. If the bar magnet in exercise 5.13 is turned around by where will the new null points be located?
Ans. The magnetic field on the axis of the magnet at a distance d1= 14 cm, can be written as:
…(i)
Where,
M = Magnetic moment
= Permeability of free space
H= Horizontal component of the magnetic field at
If the bar magnet is turned through then the neutral point will lie on the equatorial line.
Hence, the magnetic field at a distance , on the equatorial line of the magnet can be written as:
……(2)
Equating equations (1) and (2), we get:
s
The new null points will be located 11.1 cm on the normal bisector.
13. A bar magnet of magnetic moment lies aligned with the direction of a uniform magnetic field of 0.22 T.
(a) What is the amount of work required by an external torque to turn the magnet so as to align its magnetic moment: (i) normal to the field direction, (ii) opposite to the field direction?
(b) What is the torque on the magnet in cases (i) and (ii)?
Ans. (a) Magnetic moment, M=
Magnetic field strength, B= 0.22 T
(i) Initial angle between the axis and the magnetic field,
= 0° Final angle between the axis and the magnetic field,
The work required to make the magnetic moment normal to the direction of magnetic field is given as:
(ii) Initial angle between the axis and the magnetic field,
Final angle between the axis and the magnetic field,
The work required to make the magnetic moment opposite to the direction of magnetic field is given as:
(b) For case (i):
∴Torque,
For case (ii):
∴ Torque, ss
14. Answer the following questions regarding earth’s magnetism:
(a) A vector needs three quantities for its specification. Name the three independent quantities conventionally used to specify the earth’s magnetic field.
(b) The angle of dip at a location in southern India is about .
Would you expect a greater or smaller dip angle in Britain?
(c) If you made a map of magnetic field lines at Melbourne in Australia, would the lines seem to go into the ground or come out of the ground?
(d) In which direction would a compass free to move in the vertical plane point to, if located right on the geomagnetic north or south pole?
(e) The earth’s field, it is claimed, roughly approximates the field due to a dipole of magnetic moment located at its centre. Check the order of magnitude of this number in some way.
(f) Geologists claim that besides the main magnetic N-S poles, there are several local poles on the earth’s surface oriented in different directions. How is such a thing possible at all?
Ans. (a) The three independent quantities conventionally used for specifying earth’s magnetic field are:
(i) Magnetic declination,
(ii) Angle of dip, and
(iii) Horizontal component of earth’s magnetic field
(b) The angle of dip at a point depends on how far the point is located with respect to the North Pole or the South Pole. The angle of dip would be greater in Britain (it is about 70°) than in southern India because the location of Britain on the globe is closer to the magnetic North Pole.
(c) It is hypothetically considered that a huge bar magnet is dipped inside earth with its north pole near the geographic South Pole and its south pole near the geographic North Pole.
Magnetic field lines emanate from a magnetic north pole and terminate at a magnetic south pole. Hence, in a map depicting earth’s magnetic field lines, the field lines at Melbourne, Australia would seem to come out of the ground.
(d) If a compass is located on the geomagnetic North Pole or South Pole, then the compass will be free to move in the horizontal plane while earth’s field is exactly vertical to the magnetic poles. In such a case, the compass can point in any direction.
(e) Magnetic moment, M=
Radius of earth, r=
Magnetic field strength,
Where,
= Permeability of free space =
This quantity is of the order of magnitude of the observed field on earth.
(f) Yes, there are several local poles on earth’s surface oriented in different directions. A magnetised mineral deposit is an example of a local N-S pole.
15. Answer the following questions:
(a) The earth’s magnetic field varies from point to point in space.
Does it also change with time? If so, on what time scale does it change appreciably?
(b) The earth’s core is known to contain iron. Yet geologists do not regard this as a source of the earth’s magnetism. Why?
(c) The charged currents in the outer conducting regions of the earth’s core are thought to be responsible for earth’s magnetism. What might be the ‘battery’ (i.e., the source of energy) to sustain these currents?
(d) The earth may have even reversed the direction of its field several times during its history of 4 to 5 billion years. How can geologists know about the earth’s field in such distant past?
(e) The earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km). What agencies may be responsible for this distortion?
(f) Interstellar space has an extremely weak magnetic field of the order of 10-12 T. Can such a weak field be of any significant consequence? Explain.
[Note: Exercise 5.2 is meant mainly to arouse your curiosity. Answers to some questions above are tentative or unknown. Brief answers wherever possible are given at the end. For details, you should consult a good text on geomagnetism.]
Ans. (a) Earth’s magnetic field changes with time. It takes a few hundred years to change by an appreciable amount. The variation in earth’s magnetic field with the time cannot be neglected.
(b) Earth’s core contains molten iron. This form of iron is not ferromagnetic. Hence, this is not considered as a source of earth’s magnetism.
(c) The radioactivity in earth’s interior is the source of energy that sustains the currents in the outer conducting regions of earth’s core. These charged currents are considered to be responsible for earth’s magnetism.
(d) Earth reversed the direction of its field several times during its history of 4 to 5 billion years. These magnetic fields got weakly recorded in rocks during their solidification. One can get clues about the geomagnetic history from the analysis of this rock magnetism.
(e) Earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km) because of the presence of the ionosphere. In this region, earth’s field gets modified because of the field of single ions. While in motion, these ions produce the magnetic field associated with them.
(f) An extremely weak magnetic field can bend charged particles moving in a circle. This may not be noticeable for a large radius path. With reference to the gigantic interstellar space, the deflection can affect the passage of charged particles.



Click here for class 12th Subject wise notes & Study Material
Mohd. Sharif Qualification: B.Tech (Mechanical Engineering) [Founder of Wisdom Academy] [Aim Foundation & Free-Education.In] [Engineer By Profession | Teacher By Choice] [Blogger, YouTube Creator]






