www.free-education.in is a platform where you can get pdf notes from 6th to 12th class notes, General Knowledge post, Engineering post, Career Guidelines, English Speaking Trick, How to crack an interview and lots more. ( Class 11 Chemistry Chapter 5 States of Matter Notes and NCERT Solution )

NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter

Chapter 5 States of Matter:

Section Name	Topic Name
5	States of Matter
5.1	Intermolecular Forces
5.2	Thermal Energy
5.3	Intermolecular Forces vs Thermal Interactions
5.4	The Gaseous State
5.5	The Gas Laws
5.6	Ideal Gas Equation
5.7	Kinetic Energy and Molecular Speeds
5.8	Kinetic Molecular Theory of Gases
5.9	Behaviour of Real Gases: Deviation from Ideal Gas Behaviour
5.10	Liquefaction of Gases
5.11	Liquid State

Introduction

Everything in our surroundings are known as matter. They may be the food we eat, the vehicles, the gadgets, the day to day materials that we use, the air we breathe or the water that we drink. All of these things occupy some space and have mass and volume. For instance, in classrooms the benches that the students use to sit occupy some space of the classroom. They have mass and volume and hence they can be regarded as matter.

According to the Indian philosophers matter can classified into five primitive elements. They are also known as Pancha Tatva– air, soil, fire, and water. Every living or non-living is made up these five primitive elements.

Liquid State

• A liquid has no definite shape and takes up the shape of the container in which it is kept.
• A liquid has a definite volume due to weaker intermolecular force of attraction than solids.
• They can flow from a higher lever to a lower level.
• A liquid is compressible due to larger distance between the neighbouring molecules than solid but lesser than gas.
• They have lower density.
• A liquid can diffuse into another liquid due to fact that molecules move faster in a liquid but is slower as compared to gases.

Gaseous State

• They do not have definite shape and take up the shape of the container.
• They do not possess definite volume due to weakest intermolecular forces.
• They are not rigid.
• They are easily compressible due to excess space between the particles of gas which compresses on applying pressure.
• They can easily undergo diffusion due to the fact that molecules in a gas move at a very fast rate due to which speed of diffusion is very large.
• They can flow in all possible directions.

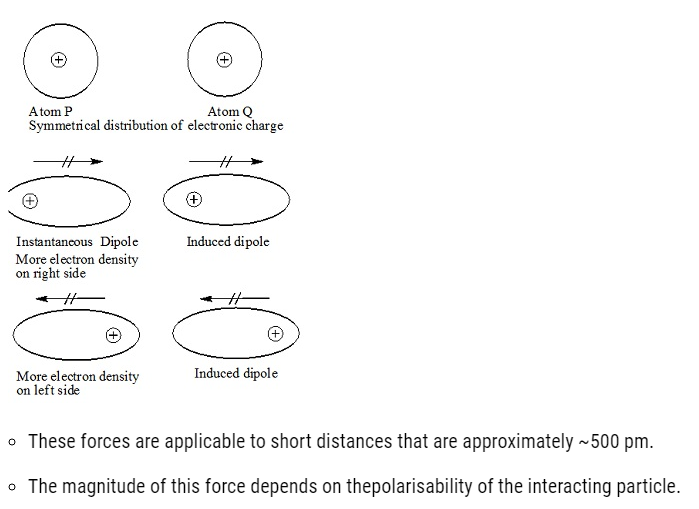
Dispersion Forces or London Forces

• Dispersion forcesor London forces refers to the attractive forces existing between the two temporary It was first proposed by a Germanphysicist Fritz London.
• These forces are always attractive.

Charles’ Law

• It states that for a fixedmass of a gas at constant pressure, volumeof a gas increases on increasing temperatureand decreases on cooling. Mathematically,

V/T = k

• Let V₁ = initial volume

 T₁ = initial temperature

After performing the experiment let V₂ = final volume

T₂ = final temperature

Hence, V₁ ÷ T₁ = k

Again V₂ ÷ T₂ = k

Since k = k, it can be concluded 

V₁ / T₁ = V₂ / T₂

Solution: According to Charles’s law

V₂/T₂  =  V₁/ T₁

Volume of gas expelled out = V₂ – V₁ ……………….. (I)

Fraction of gas expelled out = (V₂ – V₁₎ / V₂ = 1- (V₁/ V₂)     ……………. (II)

From equation (I) V₁/ V₂ = T₁/ T₂   ………….. (III)

Putting the values of (III) in (II)

Fraction of the air expelled out = 1- T₁/ T₂ = (T₂ – T₁)/ T₂

 = 750- 300 /750 = 0.6

Fraction of air expelled out is 0.6 or 3/5 th

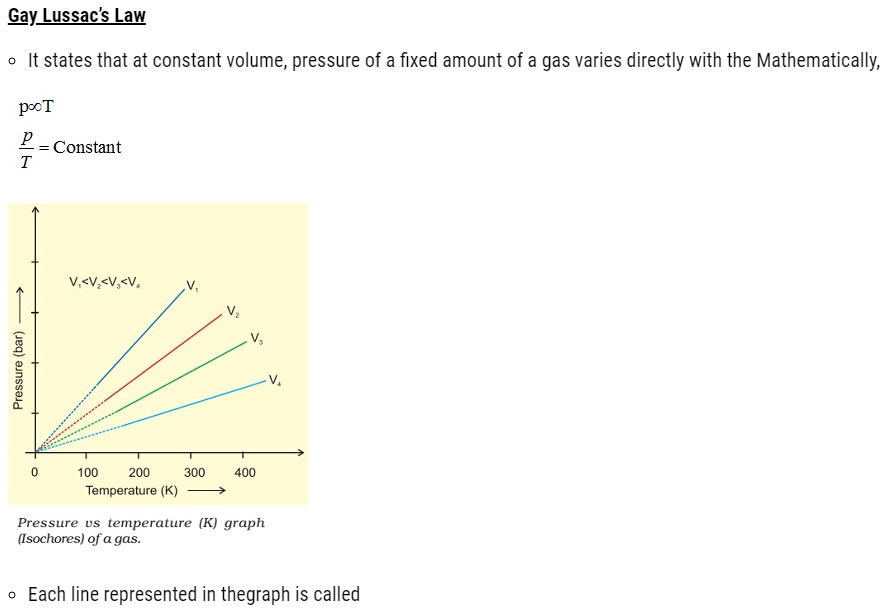
Avogadro Law

• It states that equal volumes of all gases under the same conditions of temperature and pressure
  contain equal number of molecules. Mathematically,

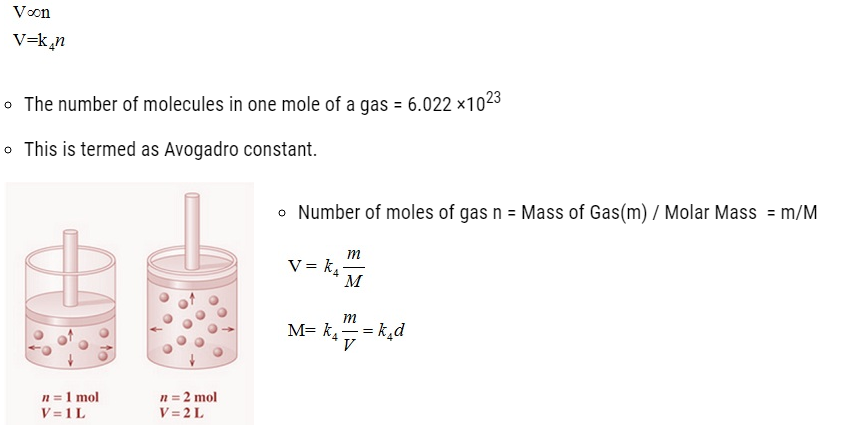
Ideal Gas Equation

• The gases following Boyle’s law, Charles’law and Avogadro law firmly are termed as anideal gas.
• From Boyle’s law we have  V ∝ 1/p (Constant T, n)
• From Charles’ law we have  V ∝ T (Constant p, n)
• From Avogadro’s law we have V ∝ n (Constant T, n)
• Combining them we get,  V ∝ nT/p
• or V = nRT/p 

pV = nRT ………………………… (IDEAL GAS EQUATION)

R =pV/nT

R= Gas Constant. It is same for all gases.

Problem:

Using the equation of state pV = nRT; show that at a given temperature density of a gas is proportional to gas pressure.

Solution:

Using Ideal gas equation, pV = nRT ……….. (1)

p → Pressure of gas

V → Volume of gas

n→ Number of moles of gas

R → Gas constant

T → Temperature of gas

From equation (1),

p = n RT/V

n = Mass of Gas (m) /Molar Mass of gas (M)

Putting value of n in the equation, we have

 p = m RT/ MV ————(2)

Density (ρ) = m /V —————-(3)

Putting (3) in (2) we get

p = ρ RT / M

Or ρ = PM / RT

Problem:

Calculate the total pressure in a mixture of 8 g of dioxygen and 4 g of dihydrogen confined in a vessel of 1 dm³ at 27°C. R = 0.083 bar dm3 K^–1 mol^–1.

Solution:

m (Oxygen) = 8 g,

M (Oxygen) = 32 g/mol

m ( Hydrogen) = 4 g,

M (Hydrogen) = 2 g/mol

n (Amount of oxygen) = 8/ 32 = 0.25 mol

n (Amount of hydrogen) = 4/2 = 2 mol

According to ideal gas equation,  

PV = n RT,

 P X 1 = (0.25 + 2) X 0.083 X 300 = 56.02 bar

Total pressure of the mixture is 56.02 bars.

Problem:

Calculate the volume occupied by 8.8 g of CO2 at 31.1°C and 1 bar pressure. R = 0.083 bar L K–1 mol^-1.

Solution:

According to ideal gas equation, PV = nRT

But n = Mass of Gas (m)/ Molar mass of Gas (M)

PV = (m/M) RT

For CO₂ , M = 44 g/mol

Putting the values

1 x V = (8.8 / 44) x 0.083 x 304.1

 = 5.05 L

Volume occupied is 5.05 L.

Density and Molar Mass of a Gaseous Substance

• As per ideal gas equation,

pV = nRT

Or n/V = p/RT

• As we know n = Mass of Gas (m) / Molar Mass of Gas (M) = m/M

So, m/MV = p/RT

d/M= p/RT

• Or Molar mass = M = dRT/p

Problem:

At 0°C, the density of a certain oxide of a gas at 2 bar is same as that of dinitrogen at 5 bar. What is the molecular mass of the oxide?

Solution:

Using the formula  ρ = Mp/RT

or p = ρ RT/ M

According to the question,

For certain oxide gas

2 = ρ RT/ M ……………(1)

For nitrogen

5 = ρ RT/28 ………………….(2)

From equation (1) & (2), we get

5/2 = M/28

Or

M = 5 X 28/ 2 = 70g/mol

Problem:

Density of a gas is found to be 5.46 g/dm3 at 27 °C at 2 bar pressure. What will be its density at STP?

Solution:

According to the ideal gas

Density ρ = p x M/ RT

According to the question,

5.46 = 2 x M/ 300 x R    ……… (1)

ρ_STP = 1 x M/ 273 x R    ……….. (2)

From equation (1) & (2),

ρ_{STP =}  (1 x M/ 273 x R)   x (300 x R/ 2 x M) = 300 / 273 X 2 = 3.00 g/dm³

Density of the gas at STP will be 3 g dm^–3.

Problem:

Calculate the total number of electrons present in 1.4 g of dinitrogen gas.

Solution:

m ( Nitrogen) = 1.4 g

M (Nitrogen) = 28 g mol^–1

n (Amount of nitrogen) = 1.4 / 28 = 0.05 mol

Hence number of nitrogen molecule in 0.05 mol = 6.023 x 10²³  x 0.05 = 3.0115 x 10²²

Number of electrons in one molecule of nitrogen = 14

Total number of electrons in 1.4 g of nitrogen = 3.0115 x 10²² x 14  = 4.22 x 10²³

Partial pressure in terms of mole fraction

• Let three gases be enclosed at

T = temperature three gases,
V = volume,
p1, p2 and p3 = partial pressure exerted on three gases respectively.

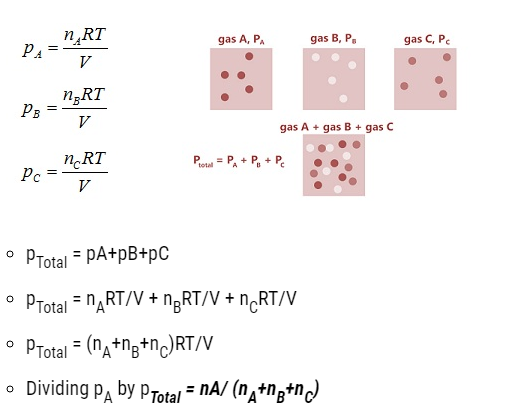
• P_{A =} x_A p_Total

Similarly, p_{B =} x_B p_Total

P_{C =} x_C p_Total

Problem:

A mixture of dihydrogen and dioxygen at one bar pressure contains 20% by weight of dihydrogen. Calculate the partial pressure of dihydrogen.

Solution:

Pressure of the gas mixture = 1 bar

Let the amount of mixture = 100g

Mass of hydrogen in mixture = 20 g

Mass of oxygen in mixture = 80 g

n_H = 20/ 2  = 10 mol

n_O = 80 / 32 = 2.5 mol

Using the formula,

p_H = X_H x P_total = (n_H / n_{H +} n_O) x P _total   = (10 / 10 + 2.5 ) x  1 

= 0.8 bar

Kinetic molecular theory of gases

• Molecules are point masses having no volume.
• Gas atoms apply no constrain on different atoms unless they suffer collision.
• Collisions of particles with each other or with the boundaries of container do not result in decreased energy system.
• The atoms of a gas are in consistent and irregular movement.
• The temperature of a gas relies upon its average kinetic energy 1/2 mv² = 3/2 KT
• Ideal gas possesses kinetic energy.

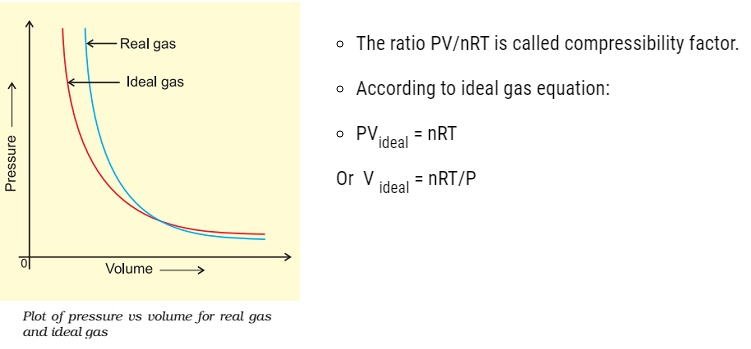
Behaviour of real gases: deviation from ideal gas behaviour

• The isotherm obtained in the graph by plotting the pressure (P) vs Volume (V) for real gas does not coincide with the slope of ideal gas.

Viscosity

• Viscosity refers to the resistance to the flow of liquid arising as a result of the internal friction within the layers as they pass over other layer.
• Viscosity arises due to the strong intermolecular forces between the molecules that holds them together and resist the passing of layers over other.
• The layers of molecules of the flowing liquid that are in contact with the surface are stationary.
• Increase in the distance between the two layers increases the velocity of the upper layer.
• Flow of liquid with regular gradation of velocity while passing over other layer is termed as laminar flow.

• It is equal to the force when the velocity gradient and area of contact is unity. Therefore, η can be called the measure of viscosity.
• It is measured in unit called Nsm^-2.

Problem:

A liquid is streaming between two layers. Figure the shearing power if the shear speed is 0.25 m/s and has length 2 m and element thickness is 2Ns/m2.

Solution:

d u = 0.25 m/s,

d z = 0.125/s

η = 2 Ns/m^2

F = η A du/dz

F = 2 Ns/m² × 0.125 /s

F = 0.5 N/m² 

Related link you must like:-

HVAC Course

CBSE Study Material

Study material for Competition Exam

Interview Question

Career Option

Spoken English

CBSE Website