Class 12 Chemical Kinetics , In this post We will Study, Chemical Kinetics Notes & Important Topic for Student to excel in exam.
NCERT/CBSE class 12th Chemistry notes provided by free-education.in (Wisdom Education Academy). Here We are providing all subject wise pdf notes to student for their help to get good marks in exam. In this post you will get Download CBSE 2020-21 Chemistry PDF notes given below by free-education.in to excel in the exam.
www.free-education.in is a platform where you can get pdf notes from 6th to 12th class notes, General Knowledge post, Engineering post, Career Guidelines , English Speaking Trick , How to crack interview and lots more.
Introduction
The stream of chemistry that governs the rate of reactions along with their mechanisms is termed as Chemical kinetics derived from a Greek word meaning chemical movement.
Combination of two or more reactants to produce a new product is called reaction.
Elementary Reaction:
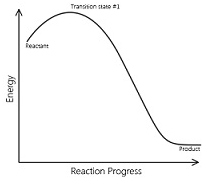
The reaction that occurs in a single step to give the product is called an elementary reactions.
Complex reaction:
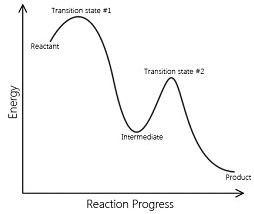
The reactions that occur as a result of sequence of elementary reactions to give the product is called complex reactions.
Rate of reaction
The rate at which the concentration of reactant or product participating in a chemical reaction alters is called rate of reaction.
Rate of reaction = change in concentration/ time = (mol/litre)/time
Reactant (R) –> Product.
Rate [R]
Rate = k[R]
k = rate constant or velocity constant.
Let one mole of the reactant A produce one mole of the product B.
Let at time t1
[A]1 and [B]1 = Concentrations of A and B
Let at time t2
[R]2 and [P]2 = Concentrations of A and B
Rate of disappearance of A = Decrease in concentration of R / Time taken = -∆[A]/∆t
Rate of appearance of B = Increase in concentration of P / Time taken = +∆[B]/∆t
When two or more reactants combine with each other the molecules of the respective reactants collide with each other to form the product. The collision between the molecules increases with the increase in concentration of the reactants and thereby increases the rate of reaction. A + B –> C + D
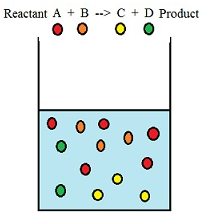
Here molecules of reactant A and B collide to produce molecules of product C and D.
Therefore we can conclude that rate of reaction is directly proportional to the concentration of the participating reactants.
Rate ∝ [A]x [B]y
Or Rate = k[A]x [B]y
Hg(l) + Cl2 (g) –> HgCl2(s)
Rate of reaction= -∆[Hg]/∆t = ∆[Cl2]/∆t = ∆[Hg Cl2]/∆t
Factors affecting rate of reaction
Nature of reactant
Nature of bonding in the reactants determines the rate of a reaction. The ionic compounds react faster compared to covalent compounds due to requirement of energy in covalent compounds to cleave the existing binds.
The reaction between ionic compounds:
Precipitation of AgCl
AgNO3 + NaCl –> AgCl + NaNO3
The reactions between covalent compounds:

Temperature
Rate of reaction increases with the rise in temperature due to increase in average kinetic energy which in turn increases the number of molecules having greater energy than threshold energy and consequently increasing the number of effective collisions. The rate of a reaction is doubled (i.e., increased by 100%) with 10 oC rise in temperature.
Pressure
Increase in partial pressure increases the number of collisions. Therefore, the rate of reactions involving gaseous reactants increases with the increase in partial pressures.
Catalyst
A catalyst increases the rate of reaction by giving an alternative path with lower activation energy (Ea’) for the reaction to proceed.
Concentration of reactants
Increase in concentration increases the number of collisions and the activated collisions between the reactant molecules. According to the collision theory, rate is directly proportional to the collision frequency. Consequently, the rate of a reaction increases with the rise in the concentration of reactant.

Surface area
The rate of a reaction increases with increase in the surface area of solid reactant.
PROBLEM. For the reaction: 2A + B → A2B , The rate = k[A][B]2with k= 2.0 x 10-6mol-2L2s-1. Calculate the initial rate of the reaction when [A] = 0.1 mol L-1, [B] = 0.2 mol L-1. Calculate the rate of reaction after [A] is reduced to 0.06 mol L-1.
SOLUTION. Rate = k [A][B]2
= (2.0 × 10 – 6mol – 2L2s – 1) (0.1 mol L – 1) (0.2 mol L – 1)2
= 8.0 × 10 – 9mol – 2L2s – 1
Reduction of [A] from 0.1 mol L – 1to 0.06 mol – 1
The concentration of A reacted = (0.1 – 0.06) mol L – 1 = 0.04 mol L – 1
The concentration of B reacted= 1/2 x 0.04 mol L-1 = 0.02 mol L – 1
The concentration of B available, [B] = (0.2 – 0.02) mol L – 1
= 0.18 mol L – 1
After reduction of [A] to 0.06 mol L – 1
The rate of the reaction
Rate = k [A][B]2
= (2.0 × 10 – 6mol – 2L2s – 1) (0.06 mol L – 1) (0.18 mol L – 1)2
= 3.89 mol L – 1s – 1
Average rate of reaction
The average rate of the reaction is the ratio of change in concentration of reactants to the change in time. It is determined by the change in concentration of reactants or products and the time taken for the change as well. As the reaction precedes forward the collisions between the molecules of the participating reactants reduces thereby decreasing the average rate of the reaction.
Mathematically, Average rate of reaction = Change in concentration / Time = (mol/litre)/time
PROBLEM. For the reaction R → P, the concentration of a reactant changes from 0.03 M to 0.02 M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds.
SOLUTION. R2= 0.02 M
R1= 0.03M
t2 – t1= 25 minutes
∆[R]/∆t =∆[R2-R1]/ t2– t1=- (0.02-0.03)/25 = 6.67 X 10-6 Ms-1
=0.005ML-1 min-1
PROBLEM. In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L-1 to 0.4 mol L-1 in 10 minutes. Calculate the rate during this interval?
SOLUTION. -1/2 (∆[A]/∆t) =-1/2(∆[A2-A1]/∆t) =-1/2 (0.4-0.5/10)
=0.005ML-1 min-1
= 5 X 10-3M min-1
Instantaneous rate of reaction
The ratio of change in concentration in chemical reaction to the time period is termed as instantaneous rate of the reaction.
-d[R]/dt = change in chemical concentration over short period of time/ the short time elapsed = (mol/litre) / time
It can be calculated from the slope of the tangent on a concentration- time graph.
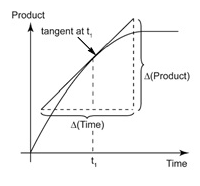
For example, consider the following graph.
The rate of reaction at t = 40s in the above graph can be calculated by following method:
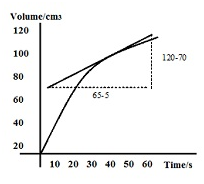
Rate of reaction = gradient of the tangent at 40s = (120-70)/(65-5) = 50/60= 0.83 cm3s-1
Rate expression
The representation of rate of reaction in terms of concentration of the reactants is called rate equation or rate expression.
For example, in the reaction
2NO(g) + O2(g) –> 2NO2
The rate expression is given as
Rate =k[NO]2[O2]
Let us consider another reaction
BrO3– + 5Br– + 6H+ –> 3Br + 3 H2O
Rate expression for this reaction is given as
k[BrO3–][Br–][H+]2
Order of a reaction
The addition of power of the concentration of reactant in a rate law expression gives the order of reaction.
Let A + 2B –> C + D be a chemical reaction.
From rate law R = k [A]x [B]y
Now Order of reaction is defined as addition of the order of all the reactants participating in a chemical reaction.
order w.r.t. A = x
Order w.r.t. B = y
Overall order of the given reaction = (x + y).
Units of order of reaction:
k = rate / [A]n = (mol.L-1s-1/molL-1) n
For 1st order reaction , n=1
k = rate / [A]1 = (mol.L-1s-1/molL-1) 1= s-1
For 2nd order reaction, n=2
k = rate / [A]2 = (mol.L-1s-1/molL-1) 2= L.mol-1s-1
PROBLEM. From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
(i) 3 NO(g) → N2O(g) Rate = k[NO]2
(ii) H2O2 (aq) + 3 I – (aq) + 2 H+→ 2 H2O (l) + I3– Rate = k[H2O2][I – ]
(iii) CH3CHO(g) → CH4(g) + CO(g) Rate = k [CH3CHO]3/2
(iv) C2H5Cl(g) → C2H4(g) + HCl(g) Rate = k [C2H5Cl]
SOLUTION. (i) Rate = k[NO]2
Order of the reaction = 2
Dimension of k = Rate / [NO]2
= mol L-1 s-1 / (mol L-1)2
= mol L-1 s-1 / mol2 L-2
= L mol-1 s-1
(ii) Rate = k[H2O2][I – ]
Order of the reaction = 2
Dimension of k = Rate / [H2O2][I – ]
= mol L-1 s-1 / (mol L-1) (mol L-1)
= L mol-1 s-1
(iii) Rate =k [CH3CHO]3/2
Order of reaction = 3/2
Dimension of k = Rate / [CH3CHO]3/2
= mol L-1 s-1 / (mol L-1)3/2
= mol L-1 s-1 / mol3/2 L-3/2
= L½ mol-½ s-1
(iv) Rate = k [C2H5Cl]
Order of the reaction = 1
Dimension of k = Rate / [C2H5Cl]
= mol L-1 s-1 / mol L-1
= s-1
PROBLEM. For a reaction, A + B → Product; the rate law is given by, r = k [A]½ [B]2. What is the order of the reaction?
SOLUTION. The order of the reaction = 1/2 + 2
= 2 1/2
= 2.5
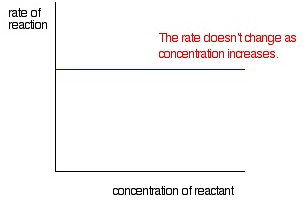
Zeroth order reaction
If the rate of reaction is independent of concentration of the reactant participating in the reaction then the reaction is called Zeroth order reaction.
A –> B
At time t = 0 concentration of A (reactant) is a and B (product) is 0. At time t = t the concentration of A (reactant) is (a-x) and that of B (product) is x.
-d[A]/dt = k0[A]0 => dx/dt = k0(a-x)0
dx/dt = k0
∫ 0x dx =k0 ∫0 xdt
X = k0t
PROBLEM. The decomposition of NH3on platinum surface is zero order reaction. What are the rates of production of N2and H2if k = 2.5 x 10-4mol-1L s-1?
SOLUTION. 2NH3 –> N2 + 3H2
Rate of zero order reaction
-1/2 (d[NH3]/dt) = d[N2]/dt = 1/3 (d[H2]/dt)
-1/2 (d[NH3]/dt) = d[N2]/dt = 1/3 (d[H2]/dt)= k = 2.5 x 10-4 mol L-1 s-1
Rate of production of N2
d[N2]/dt = 2.5 x 10-4 mol L-1 s-1
Rate of production of H2
d[H2]/dt = 3 x 2.5 x 10-4 mol L-1 s-1
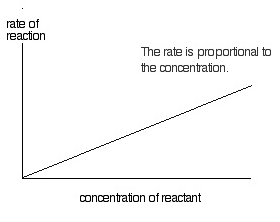
First order reaction
If the rate of reaction depends on the concentration of single reactant participating in chemical reaction raised to the first power then it is called a first order reaction.
A –> B
At time t = 0 concentration of A (reactant) is a and B (product) is 0. At time t = t the concentration of A (reactant) is (a-x) and that of B (product) is x.
-dx/dt ∝ (a-x) = dx/dt = k1(a-x)
∫ 0x dx/(a-x) = k1∫ 0t dt
dx/dt = k0(a-x)0
dx/dt = k0
∫0 x dx = k0∫ 0t dt
ln (a/a-x) = k1t => t = 1/ k1 ln (a/a-x) = 2.303/ k1 log (a/a-x)
k1 = 2.303 log (a/a-x)
PROBLEM. A first order reaction has a rate constant 1.15 10-3s-1. How long will 5 g of this reactant take to reduce to 3 g?
SOLUTION. From the question, we can write down the following information:
Initial amount = 5 g
Final concentration = 3 g
Rate constant = 1.15 10 – 3s – 1
We know that for a 1st order reaction,
t = (2.303/k)log[R0]/[R]
(2.303/1.15X10-3)log[5]/[3]
(2.303/1.15X10-3) X 0.2219 = 444.38 s = 444 s
Second order reaction
A reaction with order equal to two is called a second order reaction.
r = k[A]2
or r = k [A][B]
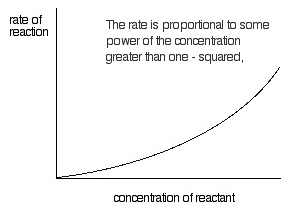
Pseudo order reaction
The reaction that appears to be an nth order reaction but belongs to some different order is called Pseudo order reaction.
For example, a pseudo first order reaction is a chemical reaction between two reactants participating in a chemical reaction and therefore should be a second order reaction. But it resembles to be a first order reaction due to the presence of reactants in negligible quantity.
Let R` + R“ –> P
Rate = k[A]1[B]1
Order of reaction = 2.
Let us consider another reaction,
CH3Br + OH−→ CH3OH+Br−
Rate law for this reaction is
Rate = k [OH−][CH3Br]
Rate = k [OH−][CH3Br] = k(constant)[CH3Br]=k′[CH3Br]
As only the concentration of CH3Br would change during the reaction, the rate would solely depend upon the changes in the CH3Br reaction.
Molecularity
- As we know that molecules need to collide to bring about a chemical reaction, so the number of molecules participating in an elementary chemical reaction that collides to bring about the chemical reaction is called molecularity of a reaction.
- The value of molecularity of a reaction is always a positive value.
- Let us consider a following reaction:
A + 2B –> C + D
Here reactants are: 1 molecule of A ,2 molecules of B
Products are: 1 molecule of C , 1 molecule of D.
Therefore we can conclude that reaction is trimolecular.
A reaction with molecularity =1 is called unimolecular.
Example, PCl5 –> PCl3 + Cl2
- A reaction with molecularity =2 is called bimolecular.
Example, Cl + CH4 –> HCl + CH3
- A reaction with molecularity =3 is called trimolecular.
2FeCl3 + SnCl2 –> 2FeCl2 + SnCl4
- It is theoretical value and does not determine the rate of reaction. Nor does it depend upon external factors like temperature or pressure, etc.
Integrated rate equation
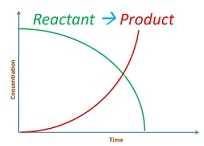
Consider the reaction
aA + bB –> cC + dD
Rate = k [A]x[B]y
-dR/dt = k[A]x[B]y
dR/dt is instantaneous rate.
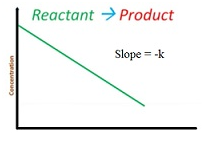
Integrated rate equation for zero order reaction
-dR/dt = k[R]0=k
dR/dt = -k
∫ dR = -k ∫ dt
[R]=-kt +I
At t = 0
R0= -k .0 + I
I = R0
So the equation becomes R = -kt + R0
Graph for this is as follows:
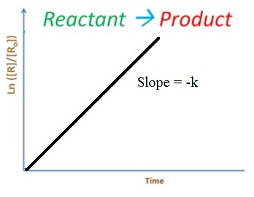
Integrated rate equation for first order reaction
Rate = -dR/dt = k[R]2
∫ dR/R= – ∫ kt
ln R = -kt + I
At t = 0
R = R0
ln R0=-k X 0 +I
I = ln R0
So equation becomes
ln R = -kt + ln R0
ln [R0/ R]=-kt
Rate law
- The representation of rate of reaction in terms of molar concentration of the reactants participating in a reaction raised to some power is called rate law.
- It is also called rate expression or rate equation.
- Consider a reaction:
2NO (g) + O2 (g) –> 2NO2
Rate ∝ [NO]2
Rate ∝ [O2]
Combining these two rates we derive
Rate ∝ [NO]2 [O2]
Rate =k [NO]2 [O2]
- Where k is the proportionality constant with a definite value at a specific temperature for a specific reaction and is called Rate Constant.
- Rate law expression = -d[R]/ dt = k [NO]2 [O2]
Half life reactions : The time elapsed in reduction of the concentration of a reactant participating in a chemical reaction to one half of its original concentration is called half-life reaction and is represented by t1/2.
Half-life for zero order reactions:
A –> B
At time t = 0 concentration of A (reactant) is a and B (product) is 0. At time t = t the concentration of A (reactant) is (a-x) and that of B (product) is x.
x = k0t à a/2 = k0t1/2 = a/2k0
t1/2 =a/2k0
a=(2k0)(t1/2)
y = mx
t = Independent variable. It is taken at x-axis.
m = 2k0
Half-life for first order reactions:
t = 2.303/k1 log a/(a-x)
For half-life x = a/2; t = t 1/2
t ½ = 2.303/k1 log a/(a-a/2) –> t1/2 = 2.303/k1 log2
t ½ = 2.303/k1 X 3.010
t ½ = 0.693/ k1
Rate determining step
- The slowest step during a chemical reaction determines the overall speed of a reaction towards completion is called rate determining step.
- Let us consider the following reaction,
NO2(g)+CO(g)→NO(g)+CO2(g)
- The elementary steps of the reaction are as follows:
Step 1: NO2+NO2→NO+NO3 (Rate constant = k1, slow)
Step 2: NO3+CO→NO2+CO2 (Rate constant = k2, fast)
- As the first step is the slowest step in the reaction it will determine the rate of the overall reaction. Therefore Step1 is the rate determining step of the given reaction and hence the rate expression for the given reaction is the product of rate constant and the reactants of this step.
Rate = k1[NO2][NO2]=k1[NO2]2
Activation energy
- The minimum quantitiy of external energy required for the conversion of reactant into product or to produce an unstable intermediate is called activation energy. It is E
- Rate of reaction is inversely proportional to the activation energy.
- Therefore, greater value of activation energy leads to lower rate of reaction and increased influence of temperature change on the rate constant.
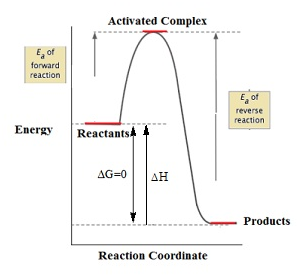
PROBLEM. The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate ESolution.
SOLUTION. It is given that T1 = 298 K
∴T2 = (298 + 10) K
= 308 K
We also know that the rate of the reaction doubles when temperature is increased by 10°.
Therefore, let us take the value of k1 = k and that of k2 = 2k
Also, R = 8.314 J K – 1 mol – 1
Now, substituting these values in the equation:
Log k2/k1 = Ea/2.303R [T2-T1/T1T2]
Log 2k/k = Ea/2.303 X 8.314 [10/298 X 308]
Ea= 2.303 X 8.314 X 298 X 308 X log2/10
= 52897.78 J mol – 1
= 52.9 kJ mol – 1
Arrhenius equation
- The formula used to calculate the energy of activation and justify the effect of temperature on rate of reaction is called Arrhenius Equation.
- It is given by the formula,
K = A e-Ea/RT
Where,
k = Rate constant
A= Frequency factor
e = mathematical quantity
Ea= activation energy
R = gas constant
T = kelvin temperature
ln K = ln A – Ea/(2.303RT)
Equation of a straight line with slope = –Ea /R.
- When Ea = 0 , Temperature = Infinity
K = Ae0 = A
e-Ea/RT =Boltzmann factor.
- For a chemical reaction the rate constant gets doubled for a rise of 10° temperature. This is because according to Arrhenius Equation,
K = Ae-Ea/RT
Taking log on both sides of the equation
Ln k = ln A – Ea/RT
Comparing with the equation of a straight line
y= mx+c,
[m= slope of the line
c= y-intercept]
So we have:
y = ln k
x = 1/T
m = -Ea / R
c = ln A
Plotting k Vs (1/T)
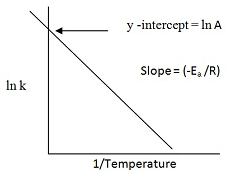
PROBLEM. Find the activation energy (in kJ/mol) of the reaction if the rate constant at 600K is 3.4 M-1 s-1 and 31.0 at 750K.
SOLUTION. Ln k = ln A – Ea/RT
To find Ea, subtract ln A from both sides and multiply by -RT.
Ea = (ln A – ln k)RT
Collision theory
- It states that:
- According to collision theory the molecules collides with great kinetic energy in order to bring about a chemical reaction.
The molecules of the reacting species collide through the space in a rectilinear motion.
Rate of a chemical reaction is proportional to the number of collisions between the molecules of the reacting species.
The molecules must be properly oriented.
- Rate of successful collisions ∝ Fraction of successful collisions X Overall collision frequency.
- The number of collisions per second per unit volume of the molecules in a chemical reaction is called collision frequency (Z).
Let A+B –> C + D
Rate = ZABe-Ea/RT
Here ZAB = collision frequency of A and B.
- In many reactions Rate = P ZABe-Ea/RT
Where p= steric factor which takes into account the proper orientation of the molecules participating in a chemical reaction.

PROBLEM. The activation energy for the reaction 2HI(g) → H2 + I2(g) is 209.5 kJ mol-1 at 581 K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
SOLUTION. Ea = 209.5 kJ mol – 1 = 209500 J mol – 1
T = 581 K
R = 8.314 JK – 1 mol – 1
Fraction of molecules of reactants having energy equal to or greater than activation energy is as follows:
x = e-Ea/RT
ln x = -Ea/RT
log x = Ea/2.303RT
log x = 209500 J mol-1/2.303 X 8.314 J K-1 mol-1 X 581 = 18.8323
x = antilog (18.323)
= antilog 19.1977
= 1.471 X 10-19
Important questions( Chemical Kinetics ):
Question 1- A reaction is of second order with respect to a reactant. How will the rate of reaction be affected if the concentration of this reactant is (i) doubled, (ii) reduced to half?
Answer: Rate = K[A]2
(i) Rate of reaction becomes 4 times
(ii) Rate of reaction will be 1/4th
Question 2- Define:
1- Elementary step in a reaction
2- Rate of a reaction
3- Order of a reaction
4- Activation energy of a reaction
5- Rate Expression
6- Rate Constant
Answer: 1. Elementary step in a reaction: The Reactions which take place in one step. Ex: H2+I2 → 2HI
2- Rate of a reaction: The change in the concentration of any one of the reactants or products per unit time.
3- Order of a reaction: Sum of powers of molar concentrations of reacting species in the rate equation of the reaction. It can be a whole number, zero, fractional, positive or negative and is experimentally determined. It is meant for the reaction and not for its individual steps.
r = K[A]x[B]y Order = x + y
4- Activation energy of a reaction: The minimum extra amount of energy absorbed by the reactant molecules to form the activated complex.
5- Rate Expression: It expresses the rate of reaction in terms of molar concentrations of the reactants with each term raised to their power, which may or may not be same as the stoichiometric coefficient of that reactant in the balanced chemical equation.
6- Rate Constant: The rate of reaction when the molar concentration of each reactant is taken as unity.
Question 3- A reaction is of first-order in reactant A and of second order in reactant B. How is the rate of this reaction affected when (i) the concentration of B alone is increased to three times (ii) the concentrations of A as well as B are doubled?
Answer: (i) r = 9 times (ii) r = 8 times
Question 4- The thermal decomposition of HCO2H is a first order reaction with a rate constant of 2.4 × 10-3 s-1 at a certain temperature. Calculate how long will it take for three-fourths of initial quantity of HCO2 H to decompose. (log 0.25 = -0.6021)
Answer: t = 577.6 seconds
{Hint- Use formula: t = (2.303 / K) log (a / a-x)}
Question 5-(a) For a reaction A + B → P, the rate law is given by, r = k[A]1/2 [B]2.
What is the order of this reaction?
(b) A first-order reaction is found to have a rate constant k = 5.5 × 10-14 s-1. Find the half-life of the reaction.
Answer: a) 5/2
b) t1/2 = 1.26 x 10 13 s
(Hint: r = k[A]1/2 [B]2 , t1/2 = 0.693/k )
Question 6- A first order gas phase reaction : A2B2(g) → 2A(g) + 2B(g) at the temperature 400°C has the rate constant k = 2.0 × 10-4 sec-1. What percentage of A2B2 is decomposed on heating for 900 seconds? (Antilog 0.0781 = 1.197)
Answer: Percent of A2B2 decomposed = 16.45 %
Question 7-For a reaction: H2 + Cl2 → 2HCl
Rate = k
(i) Write the order and molecularity of this reaction.
(ii) Write the unit of k.
Answer: (i) This reaction is zero-order reaction and molecularity is two.
(ii) Unit of k = mol L-1 s-1
Question 8- A first-order reaction has a rate constant of 0.0051 min-1. If we begin with 0.10 M concentration of the reactant, what concentration of reactant will remain in solution after 3 hours?
Answer: [R] = 0.0399 M
(Hint- Use formula: K = (2.303/t) log ([R]0/ [R])
Question 9- For a decomposition reaction the values of rate constant k at two different temperatures are given below :
k1 = 2.15 × 10-8 L mol-1 s-1 at 650 K
k2 = 2.39 × 10-7 L mol-1 s-1 at 700 K
Calculate the value of activation energy for this reaction.
(R = 8.314 J K-1 mol-1)
Answer: Ea = 182.20 KJ
(Hint- Use formula: log k2/k1 = Ea/ 2.303R [T2-T1/ T1T2]
Question 10- Nitrogen pentoxide decomposes according to equation :
2N2O5(g) → 4 NO2(g) + O2(g).
This first-order reaction was allowed to proceed at 40°C and the data below were collected :
| N2O5 (M) | Time (min) |
| 0.400 | 0.00 |
| 0.289 | 20.0 |
| 0.209 | 40.0 |
| 0.151 | 60.0 |
| 0.109 | 80.0 |
(a) Calculate the rate constant. Include units with your answer.
(b) What will be the concentration of N2O5 after 100 minutes?
(c) Calculate the initial rate of reaction.
Answer: a) K = 0.0163 min-1
b) [A] = 0.078 M
c) R = 0.00652 M min-1
Question 11- The rate of a reaction becomes four times when the temperature changes from 293 K to 313 K. Calculate the energy of activation (Ea) of the reaction assuming that it does not change with temperature. [R = 8.314 JK-1 mol-1, log 4 = 0.6021]
Answer: Ea = 52.8 KJ mol-1
(Hint- Use formula: log k2/k1 = Ea/ 2.303R [T2-T1/ T1T2]
Question 12- For the first-order thermal decomposition reaction, the following data were obtained:
C2H5Cl(g) → C2H4(g) + HCl(g)
Time/sec Total pressure/atm
0 0.30
300 0.50
Calculate the rate constant (Given: log 2 = 0.301, log 3 = 0.4771, log 4 = 0.6021)
Answer: k = 3.66 x 10-3 s-1
{Hint- k = (2.303/t) log (Po/ 2Po-Pt)}
Question 13- If the half-life period of a first-order reaction in A is 2 minutes, how long will it take [A] to reach 25% of its initial concentration?
Answer: t75 = 4 min
{Hint: t = (2.303/k) log ([A]0/ [A] }
Question 14- Define:
1- Average rate of a reaction
2- Instantaneous rate of a reaction
3- Molecularity of a reaction
4- Pseudo first-order reaction
5- Half-life period of reaction (t1/2)
6- Specific rate of a reaction
Answer:
1- Average rate of a reaction: It depends upon the change in concentration of reactants or products and the time taken for the change to occur. R → P
Average rate = – Δ[R] / Δt or Average rate = + Δ[P] / Δt
2- Instantaneous rate of a reaction: It is the rate of change in concentration of any one of the reactant or product at a particular moment of time.
limit [- Δ[R] / Δt ] = – d[R] / dt
Δt→0
3- Molecularity of a reaction: The number of atoms, ions or molecules that must collide with one another simultaneously so as to result in a chemical reaction. Molecularity of a reaction is always a whole number.
4- Pseudo first-order reaction: The reactions which are not truly of the first order but under certain conditions become first-order reactions.
5- Half-life period of reaction (t1/2): The time taken for half of the reaction to complete.
6- Specific rate of a reaction: It is the rate of reaction when the molar concentration of each of the reactants is unity.






Download Class 12th Chemistry Notes & Solution Chapter wise (Click Here)
Mohd. Sharif Qualification: B.Tech (Mechanical Engineering) [Founder of Wisdom Academy] [Aim Foundation & Free-Education.In] [Engineer By Profession | Teacher By Choice] [Blogger, YouTube Creator]






