NCERT Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments

Question 1. ( ncert solution ray optics )
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
Solution:
The object is kept between ƒ and C. So the image should be real, inverted and beyond C. To locate the sharp image, screen should be placed at the position of image.

So, the image is inverted and magnified. Thus in order to locate the sharp image, the screen should be kept 54 cm in front of concave mirror and image on the screen will be observed real, inverted and magnified. If the candle is moved closer to the mirror, the real image will move away from the mirror, hence screen has to be shifted away from the mirror to locate the sharp image.

Question 2. ( ncert solution ray optics )
A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.
Solution:
A convex mirror always form virtual image, which is erect and small in size of an object kept in front of it. Focal length of convex mirror ƒ = + 15 cm Object distance u = – 12 cm Using mirror formula

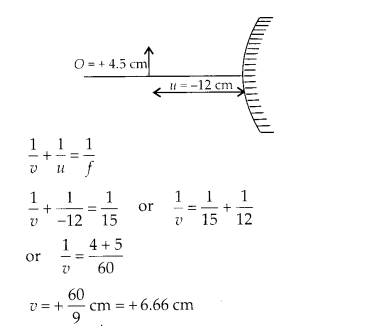
Therefore, image is virtual, formed at 6.67 cm at the back of the mirror.

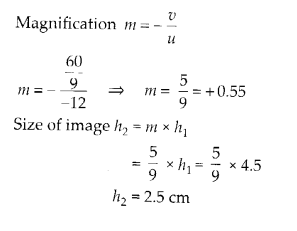
It shows the image is erect, small in size and virtual. When the needle is moved farther from mirror the image also move towards focus and decreasing in size. As u approaches v approaches focus but never beyond ƒ.

Shift = Real thickness – Apparent of thickness

Question 18.
Answer the following questions:
(a) You have learnt that plane and convex mirrors produce virtual images of objects. Can they produce real images under some circumstances? Explain.
(b) A virtual image, we always say, cannot be caught on a screen. Yet when we’see’a virtual image, we are obviously bringing it on to the ‘screen’ (i.e., the retina) of our eye. Is there a contradiction?
(c) A diver under water, looks obliquely at a fisherman standing on the bank of a lake.
(d) Does the apparent depth of a tank of water change if viewed obliquely? if so, does the apparent depth increase of decrease?
(e) The refractive index of diamond is much greater than that of ordinary glass. is this fact of some use to a diamond cutter?
Solution:
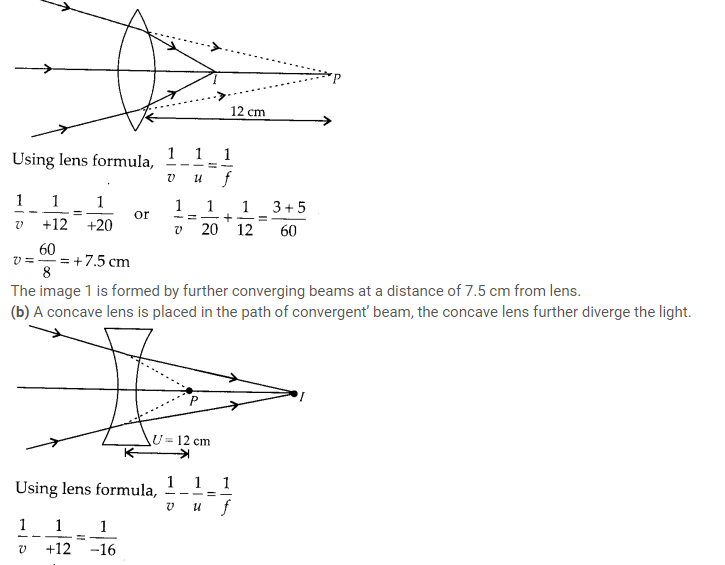
(a) In this situation when rays are convergent behind the mirror, both plane mirror and convex mirror can form real images of virtual objects.

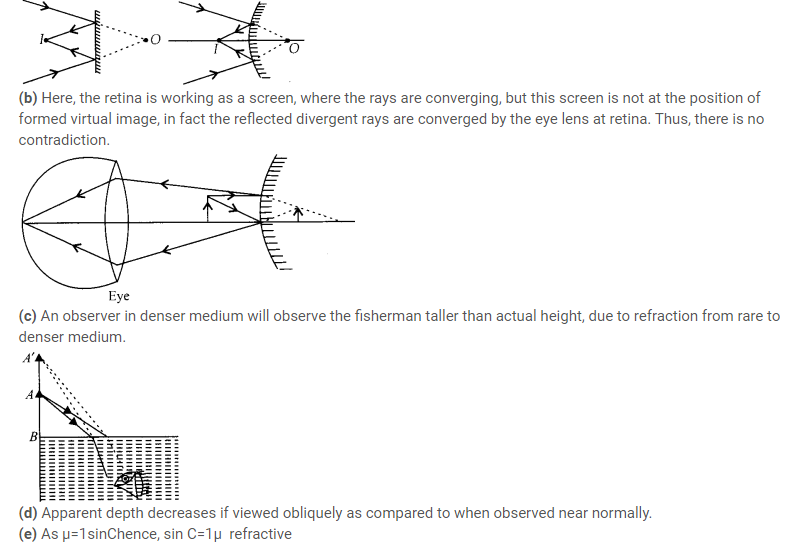
index of diamond is much greater than that of ordinary glass, hence critical angle C for diamond is much smaller (24°) as compared to that of glass (42°).
A skilled diamond cutter thus can take the advantage of such large range of angle of incidence available for total internal reflection 24° to 90°. The diamond can be cut with so many faces, to ensure that light entering the diamond does multiple total internal reflections before coming out. This behavior produce brilliance i.e., sparkling effect in the diamond.

Question 19.
The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 3 m away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?
Solution:
Let the object be placed x m in front of lens the distance of image from the lens is (3 – x) m.

Question 21.
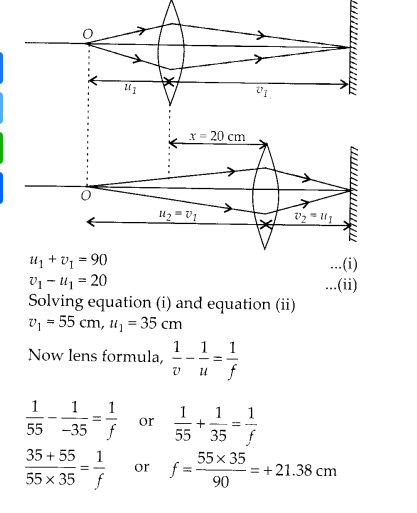
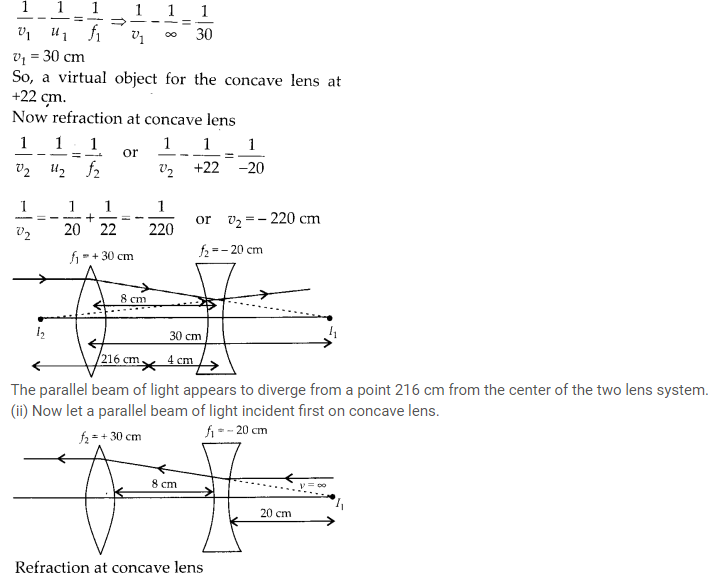
(a) Determine the ‘effective focal length of the combination of two lenses in question 10, if they are placed 8.0 cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident? Is the notion of effective focal length of this system useful at all?
(b) An object 1.5 cm in size is placed on the side of the convex lens in the above arrangement. The distance between the object and the convex lens is 40 cm. Determine the magnification produced by the two-lens system, and the size of the image.
Solution:
(a)
(i) Let a parallel beam of light incident first on convex lens, refraction at convex lens

Δθ = Δθ₁ + Δθ₂
Δθ = A₁ (μ_v1 – μ_R1) + A₂ (μ_v2 – μ_R2)

Question 24.
For a normal eye, the far points at infinity and the near point of distinct vision is about 25 cm in front of the eye. The cornea of the eye provides a converging power of about 40 dioptres, and the least converging power of the eye lens behind the cornea is about 20 dioptres. From this rough data estimate the range of accommodation (i.e., the range of converging power of the eye-lens) of a normal eye.
Solution:
Here the least converging power of eye lens is given as 20 dioptres behind the cornea. If we can calculate the maximum converging power, then we can get the range of accommodation of a normal eye.
(a) To see objects at infinity, the eye uses its least converging power = 40 + 20 = 60 dioptres
∴ Approximate distance between the retina and the cornea eyelens

Question 25.
Does short-sightedness (myopia) or long¬> sightedness (hypermetropia) imply necessarily that the eye has partially lost its ability of r accommodation? If not, what might cause these defects of vision?
Solution:
A person with normal ability of accommodation may be myopic or hypermetropic due to defective eye structure, j- When the eye ball from front to back gets too elongated the myopic defect occur, similarly when the eye ball from front to back gets too shortened the hypermetropia defect occur.
When the eye ball has normal length ‘ but the eye lens loses partially its ability of accommodation, the defect is called “presbyopia” and is corrected in the same I manner as myopia or hypermetropia.

Question 26.
A myopic person has been using spectacles of power – 1.0 dioptre for distant vision. During old age, he also needs to use separate reading glass of power + 2.0 dioptres. Explain what may have happened.
Solution:
Myopic person uses spectacles of power – 1.0 dioptre or concave lens of focal length ƒ =1p  = -100 cm in order to observe clearly object at infinity. Far point of the person can be calculated as

Question 28.
A man with normal near point (25 cm) reads a book with small print using a magnifying glass: a thin convex lens of focal length 5 cm.
(a) What is the closest and the farthest distance at which he should keep the lens from the page so that he can read the book when viewing through the magnifying glass?
(b) What is the maximum and the minimum angular magnification (magnifying power) possible using the above simple microscope?
Solution:
(a) At closest distance of the object the image is formed at least distance of distinct vision and eye is most strained.

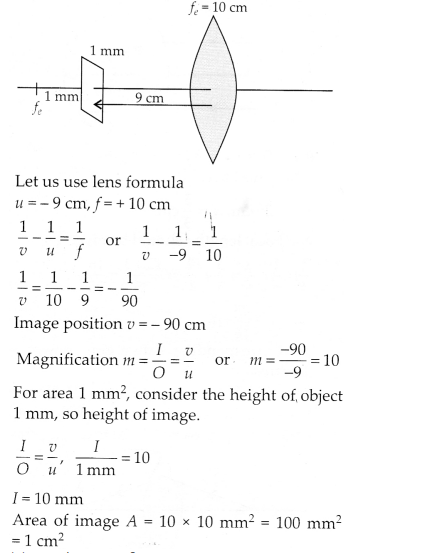
(c) If we decrease focal length, the lens has to be thick with smaller radius of curvature. In a thick lens both the spherical aberrations and chromatic aberrations become pronounced. Further, grinding for small focal length is not easy. Practically we can not get magnifying power more than 3 with a simple convex lens.

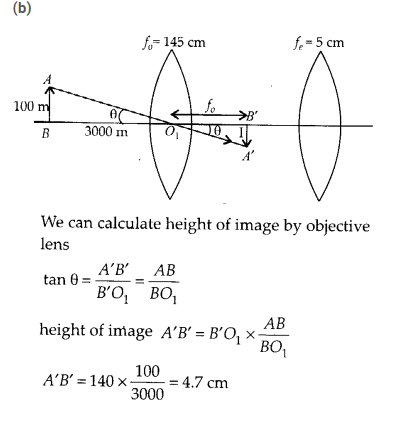
(d) Magnifying power of a compound microscope is given by

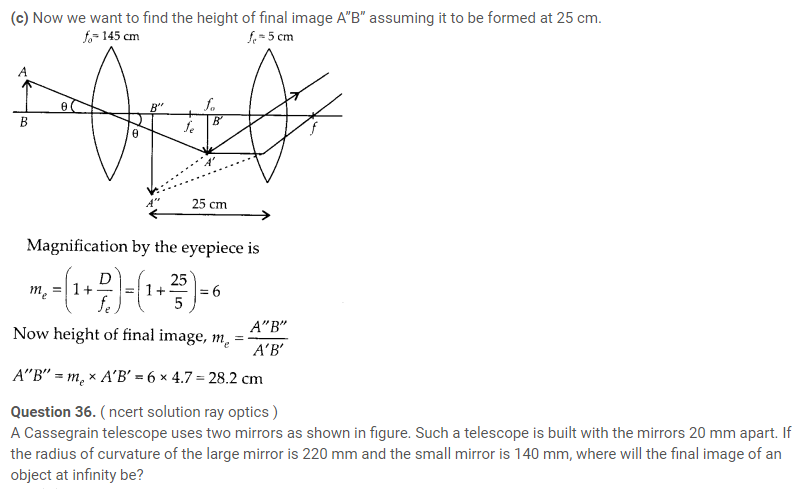
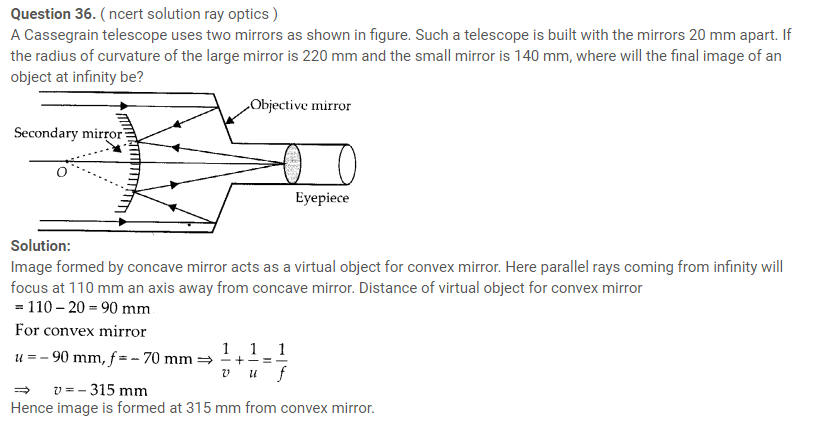
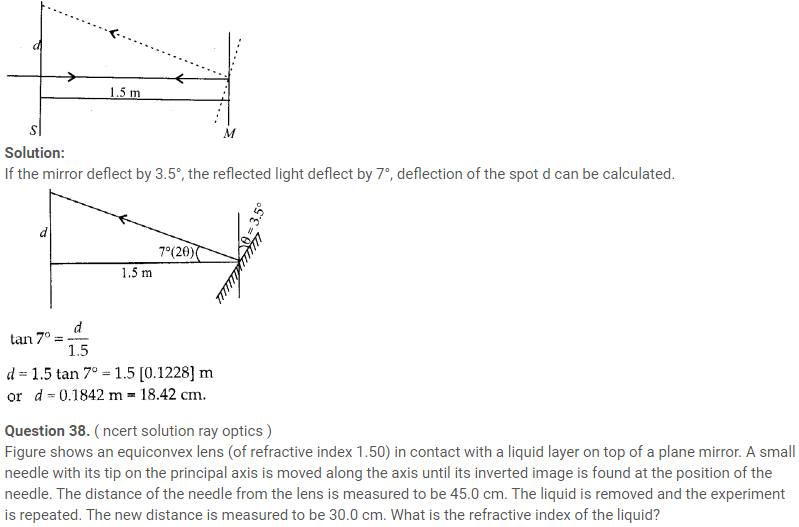
Question 37. ( ncert solution ray optics )
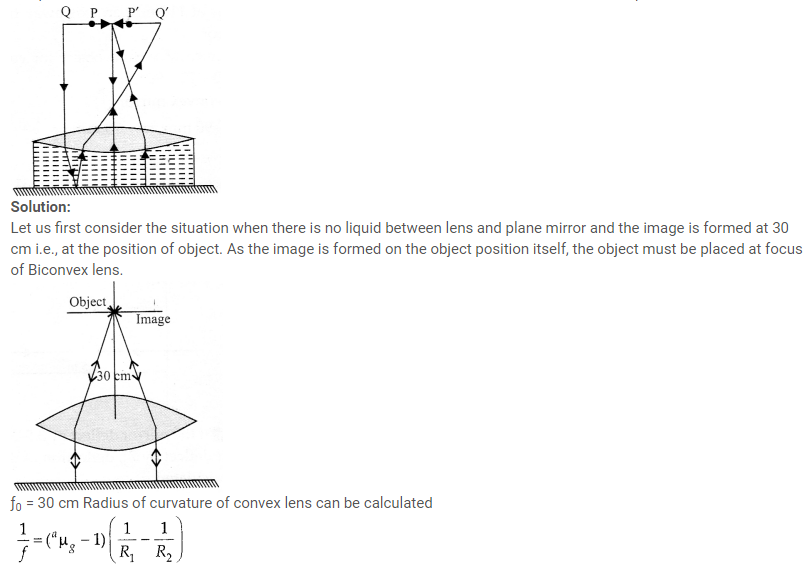
Light incident normally on a plane mirror attached to a galvanometer coil retraces backwards as shown in figure. A current in the coil produces a deflection of 3.5° of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5 m away?