www.free-education.in is a platform where you can get pdf notes from 6th to 12th class notes, General Knowledge post, Engineering post, Career Guidelines , English Speaking Trick , How to crack interview and lots more. ( Work Energy Power Class 11 Physics )
NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power (Click Here)
NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power:
| Section Name | Topic Name |
| 6 | Work Energy and power |
| 6.1 | Introduction |
| 6.2 | Notions of work and kinetic energy : The work-energy theorem |
| 6.3 | Work |
| 6.4 | Kinetic energy |
| 6.5 | Work done by a variable force |
| 6.6 | The work-energy theorem for a variable force |
| 6.7 | The concept of potential energy |
| 6.8 | The conservation of mechanical energy |
| 6.9 | The potential energy of a spring |
| 6.10 | Various forms of energy : the law of conservation of energy |
| 6.11 | Power |
| 6.12 | Collisions |
Class 11 Physics Work Energy Power Notes
Introduction
We use the words work, energy and power in our day-to-day life often. However, their meaning differ from the meaning we get from scientific definitions.

Scalar product
- The scalar product or dot product of any two vectors A and B, denoted as A.B (Read A dot B) is defined as , where q is the angle between the two vectors.
- A, B and cos θ are scalars, the dot product of A and B is a scalar quantity. Both vectors, A and B, have a direction but their scalar product does not have a direction.
- B is the product of the magnitude of A and the component of B along A. Alternatively, it is the product of the magnitude of B and the component of A along B.


Notions of Work and Kinetic Energy
- The work-energy theorem states that the change in kinetic energy of a particle is equal to the work done on it by the net force.
- Kf – Ki = W
- We know the equation in 3D : v2 – u2 = 2a.d (where u-initial velocity, v-final velocity, a-acceleration, d-displacement)
now multiplying the equation by m/2 we have, ½ mv2 – ½ mu2 = ma.d = F.d (Since ma = F)
Work
The work done by the force is defined to be the product of component of the force in the direction of the displacement and the magnitude of this displacement. W = F.d .
No work is done if:
- The displacement is zero

The force is zero.


Work done by a variable force
- The variable force is more commonly encountered than the constant force.
- If the displacement Dx is small, we can take the force F (x) as approximately constant and the work done is then
DW =F (x) Dx
For total work, we add all work done along small displacements.

Example: A force F = 3x2 start acting on a particle which is initially at rest. Find the work done by the force during the displacement of the particle from x =0m to x = 2m.

Kinetic energy
- The kinetic energy of an object is a measure of the work an object can do by the virtue of its motion.
- If an object of mass m has velocity v, its kinetic energy K is
- Kinetic energy is a scalar quantity.
The Work-Energy Theorem for a Variable Force

Example: A body of mass 0.5 kg travels in a straight line with velocity v =a x3/2 where a = 5 m–1/2 s–1. What is the work done by the net force during its displacement from x = 0 to x = 2 m
Solution: We know that WD = Kf – Ki , now we can put value of x=0 in the equation v =a x3/2 to find initial velocity, vi=0, Ki=0,
Similarly find vf by putting x=2, and Kf= ½ mv2 .
Potential energy
- Potential energy is the ‘stored energy’ by virtue of the position or configuration of a body.

Conservative & Non-Conservative Forces
- Conservative forces are those for which work done depends only on initial and final points.
Example- Gravitational force, Electrostatic force. - Non-Conservative forces are those where the work done or the kinetic energy did depend on other factors such as the velocity or the particular path taken by the object.
Example- Frictional force.

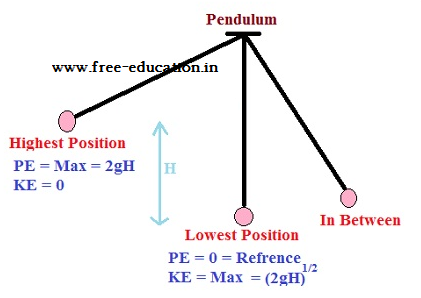
The Conservation of Mechanical Energy
- Mechanical Energy is the energy associated with the motion and position of an object.
- The quantity K +V(x), is called the total mechanical energy of the system.
- For a conservative force, ΔK = ΔW = F(x) Δx
Also, – V(x) = F(x) Δx - This employs Δ(K+V) =0 for a conservative force.
- Individually the kinetic energy K and the potential energy V(x) may vary from point to point, but the sum is a constant.
- Conservative Force:
- A force F(x) is conservative if it can be derived from a scalar quantity V(x) by the relation : F(x) = – dv/dx
- The work done by the conservative force depends only on the end points.
- A third definition states that the work done by this force in a closed path is zero.
- The total mechanical energy of a system is conserved if the forces, doing work on it, are conservative.
Potential energy of spring
- The spring force is an example of a variable force, which is conservative.
- In an ideal spring, Fs = − kx , this force law for the spring is called Hooke’s law.
- The constant k is called the spring constant. Its unit is N m-1.
- The spring is said to be stiff if k is large and soft if k is small.
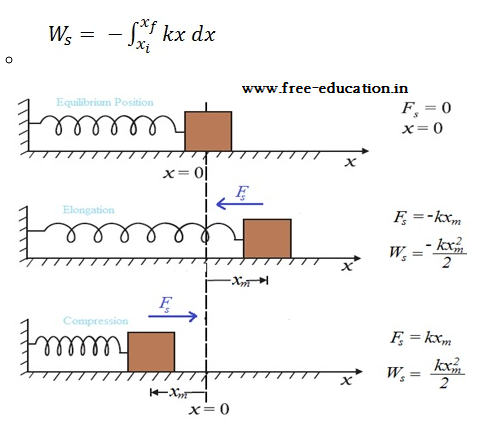
- Spring force is position dependent as first stated by Hooke, (Fs = − kx)
- Work done by spring force only depends on the initial and final positions. Thus, the spring force is a conservative force.
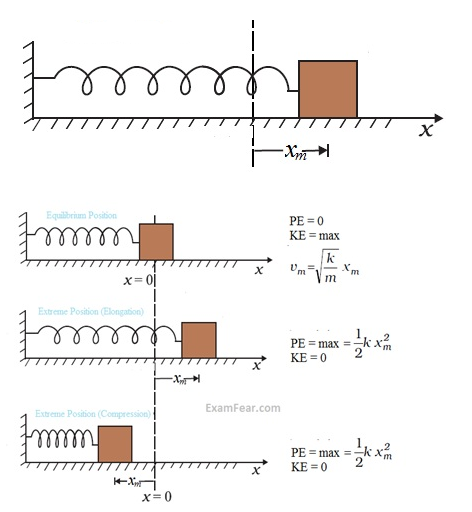
- We define the potential energy V(x) of the spring to be zero when block and spring system is in the equilibrium position.
- For an extension (or compression) x, V(x) = kx2/2
If the block of mass m is extended to xm and released from rest, then its total mechanical energy at any arbitrary point x (where x lies between – xm and + xm) will be given by:
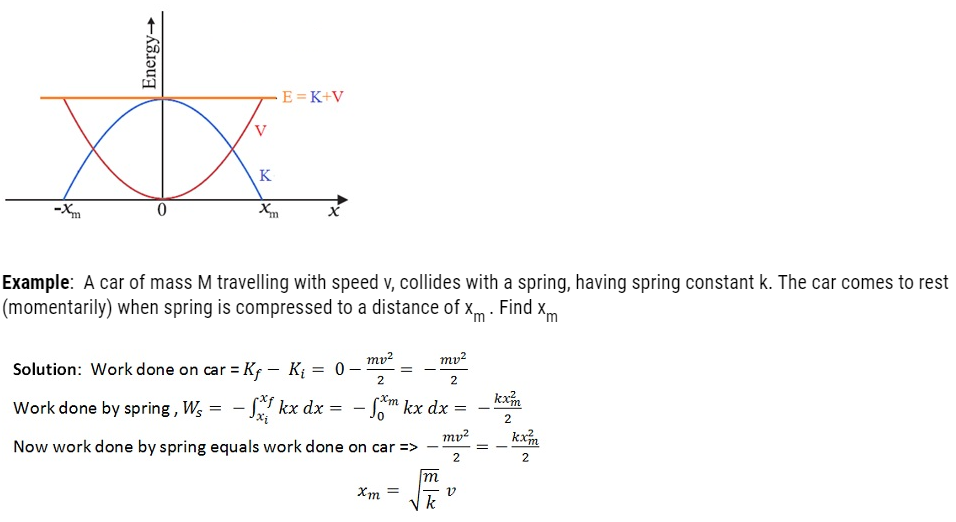
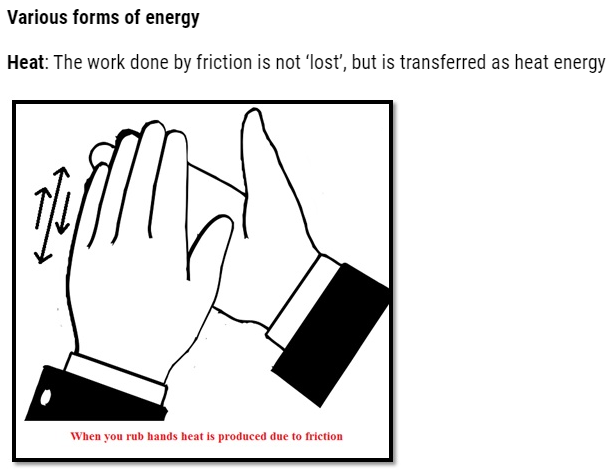
Chemical Energy:
- Chemical energy arises from the fact that the molecules participating in the chemical reaction have different binding energies.
- If the total energy of the reactants is more than the products of the reaction, heat is released and the reaction is said to be an exothermic reaction.
Example- When you freeze water you remove energy from water to lower its temperature and its phase is changed to ice, so it is a exothermic process - If the reverse is true, heat is absorbed and the reaction is endothermic.
Example- While melting the ice you provide energy to the ice to increase its tempreature and change its phase to water, so it is a endothermic process.

Nuclear Energy:
- The energy released from the nuclear reactions, either fission or fusion, is called as nuclear energy.
- Nuclear fusion and fission are manifestations of the equivalence of mass and energy.
- In fusion light atom nuclei like Hydogen fuse to form a bigger nucleus whose mass is less than the sum of the masses of the reactants.
- In fission, a heavy nucleus like uranium 235U92 , is split by a neutron into lighter nuclei. Once again the final mass is less than the initial mass and the mass difference translates into energy.

The Equivalence of Mass and Energy
- Physicists believed that in every physical and chemical process, the mass of an isolated system is conserved till Albert Einstein show the relation , E = m c2 where c, the speed of light in vacuum is approximately 3 ×108 m s–1.
- This equation showed that mass and energy are equivalent and are related by E = m c2 .
- If there is a difference between the sum of reactants and products that differene, Dm, is called mass defect.
- In case of chemical reactions the mass defect is very small and can be neglected, but in the case of nuclear reactions this becomes significant.

Principle of Conservation of Energy
- If the forces involved are non-conservative, part of the mechanical energy may get transformed into other forms such as heat, light and sound.
- However, the total energy of an isolated system does not change.
- Since the universe as a whole may be viewed as an isolated system, the total energy of the universe is constant.
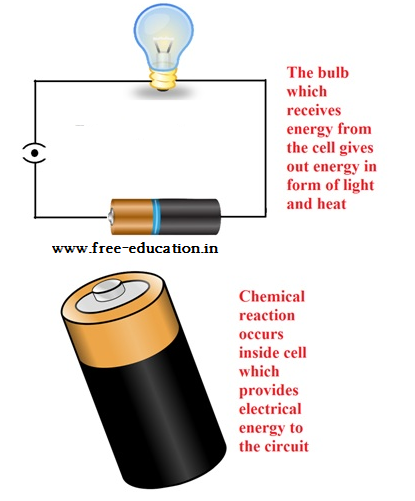
Power
- Power is defined as the time rate at which work is done or energy is transferred.




Collision in 1-D
- If the initial velocities and final velocities of both the bodies are along the same straight line, then it is called a one-dimensional collision, or head-on collision.
Elastic collision:




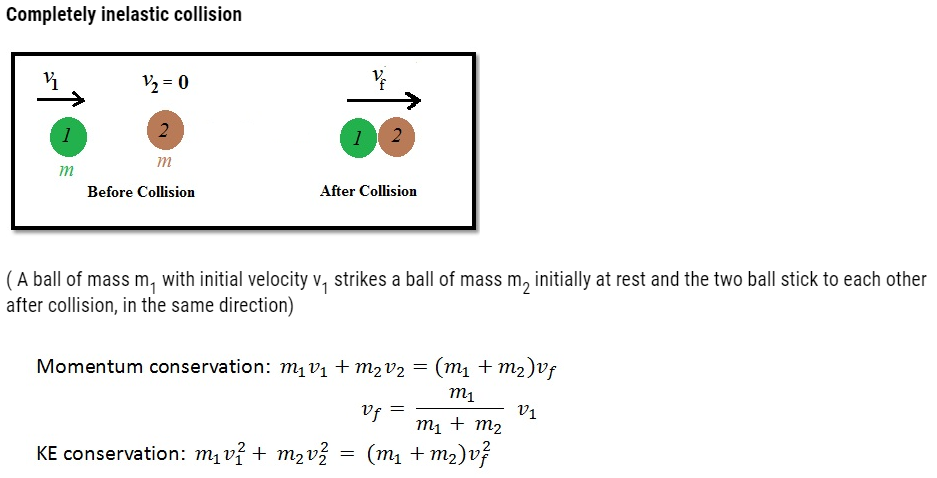
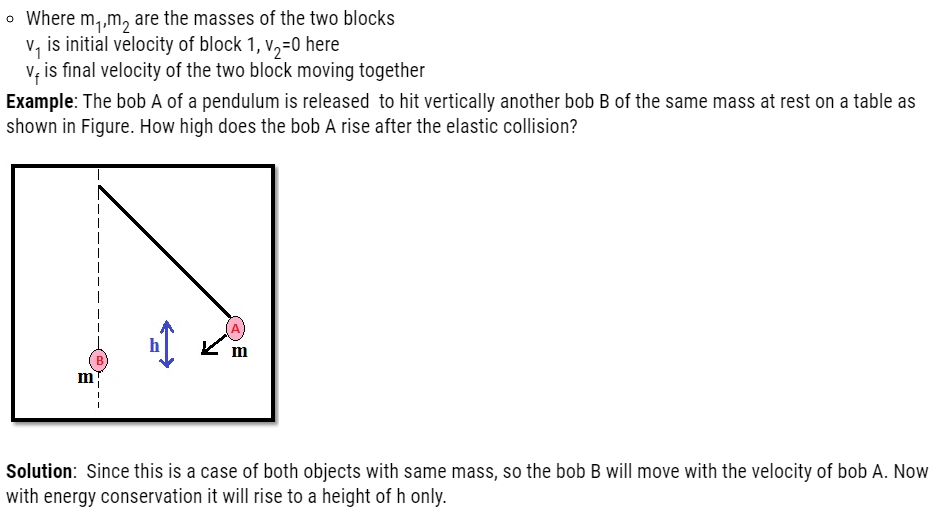

- With the above equations we have to solve the problem
Example: Two balls initially travelling along the x-axis with opposite velocities collide with each other obliquely, is it possible that they will move in the y-axis after collision?
Solution: Yes, it is possible, if the balls have same mass and travel with same speed. Initially their total momentum in x-direction was zero as their velocities were opposite; also in y-direction it is zero because they do not have velocity in that direction.
Now after collision if their velocities are still equal and in opposite direction, the total momentum still remains zero.
Related link you must like:-
Study material for Competition Exam
Mohd. Sharif Qualification: B.Tech (Mechanical Engineering) [Founder of Wisdom Academy] [Aim Foundation & Free-Education.In] [Engineer By Profession | Teacher By Choice] [Blogger, YouTube Creator]






