www.free-education.in is a platform where you can get pdf notes from 6th to 12th class notes, General Knowledge post, Engineering post, Career Guidelines , English Speaking Trick , How to crack interview and lots more. ( Class 11 Physics Motion In A Plane ) ( motion in a plane class 11 notes )

Section Name	Topic Name
4	Motion in a plane
4.1	Introduction
4.2	Scalars and vectors
4.3	Multiplication of vectors by real numbers
4.4	Addition and subtraction of vectors – graphical method
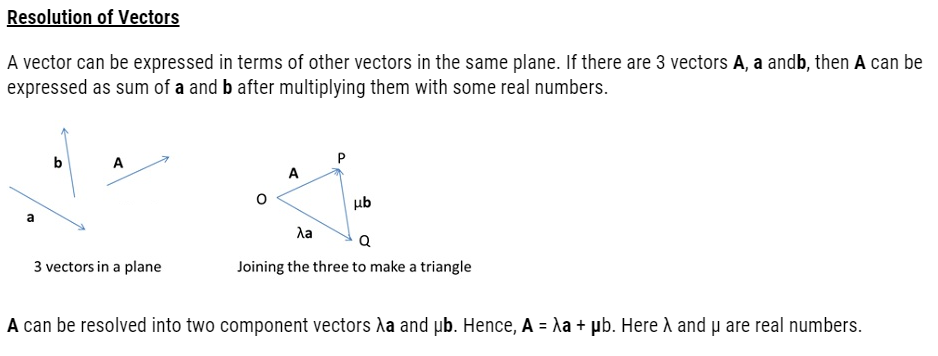
4.5	Resolution of vectors
4.6	Vector addition – analytical method
4.7	Motion in a plane
4.8	Motion in a plane with constant acceleration
4.9	Relative velocity in two dimensions
4.10	Projectile motion
4.11	Uniform circular motion

NCERT Solutions for Class 11 Physics Chapter 4 Motion in a plane

Class 11 Physics Chapter 4 Motion in a Plane

This chapter you will learn about measuring motion in a plane as well as vector and scalar quantities. You will also get to learn about diagrammatic representation of derivative laws for the addition of vector and scalar quantities. There are topics like displacement and position vector, equality of vectors, vector multiplication by real numbers, the addition of vectors through analytical methods are the topics that will be discussed in this chapter.

Motion In A Plane Notes For Exam

Scalars Vs. Vectors

Criteria	Scalar	Vector
Definition	A scalar is a quantity with magnitude only.	A vector is a quantity with magnitude and direction.
Direction	No	Yes
Specified by	A number (magnitude) and a unit	A number (magnitude), direction and a unit
Represented by	quantity’s symbol	quantity’s symbol in bold or an arrow sign above
Example	mass, temperature	velocity, acceleration

Position and Displacement Vectors

Position Vector: Position vector of an object at time t is the position of the object relative to the origin. It is represented by a straight line between the origin and the position at time t.

Displacement Vector: Displacement vector of an object between two points is the straight line between the two points irrespective of the path followed. The path length is always equal or greater than the displacement.

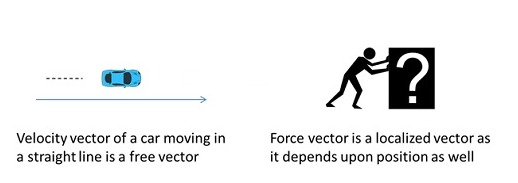
Free and Localized Vectors

A free vector(or non-localized vector) is a vector of which only the magnitude and direction are specified, not the position or line of action. Displacing it parallel to itself leaves it unchanged.

 A localized vector is a vector where line of action and position are as important as magnitude and direction. These vectors change with change in position and direction.

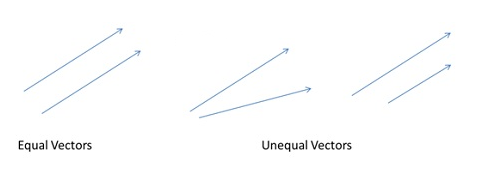
Equality of Vectors

Two vectors are said to be equal only when they have same direction and magnitude.For example, two cars travelling with same speed in same direction. If they are travelling in opposite directions with same speed, then the vectors are unequal.

Multiplication of Vectors with real numbers

Multiplication Factor	Original vector	Magnitude of vector after multiplication	Direction of vector after multiplication
λ (>0)	A	λA	Same as that of A
-λ (<0)	A	λA	Opposite to that of A
λ (=0)	A	0 (null vector)	None. The initial and final positions coincide.

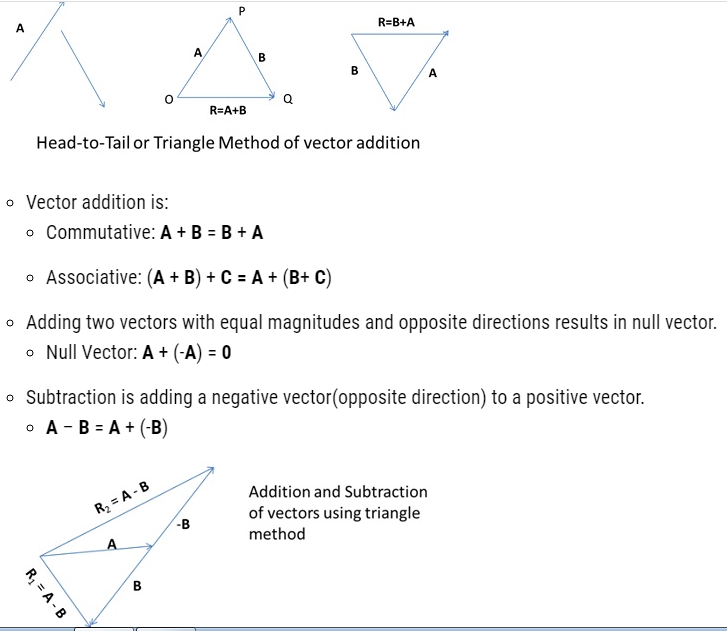
Addition and Subtraction of Vectors – Triangle Method

The method of adding vectors graphically is by arranging them so that head of first is touching the tail of second vector and making a triangle by joining the open sides. This method is called head-to-tail method or triangle method of vector addition

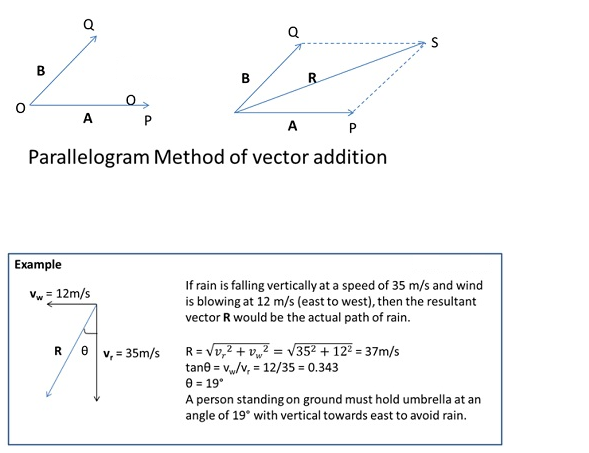
Addition of Vectors – Parallelogram Method

The method of adding vectors by parallelogram method is by:

• Touching the tail of the two vectors
• Complete a parallelogram by drawing lines from the heads of the two vectors.
• Vector resulting from the origin to the point of intersection of above lines gives the addition.

Unit Vectors

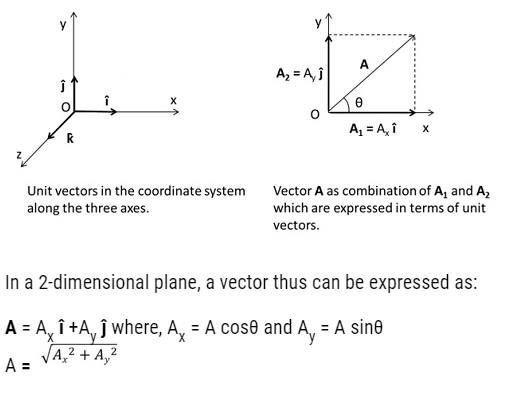
A unit vector is a vector of unit magnitude and a particular direction.

• They specify only direction. They do not have any dimension and unit.
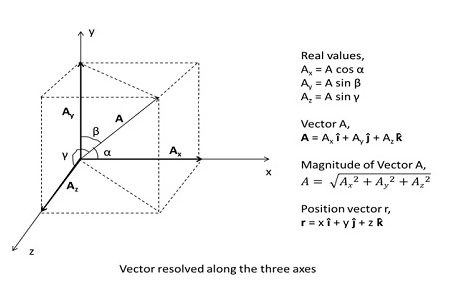
• In a rectangular coordinate system, the x, y and z axes are represented by unit vectors, î,ĵ andk̂
• These unit vectors are perpendicular to each other.
• |î| = |ĵ | = |k̂| = 1

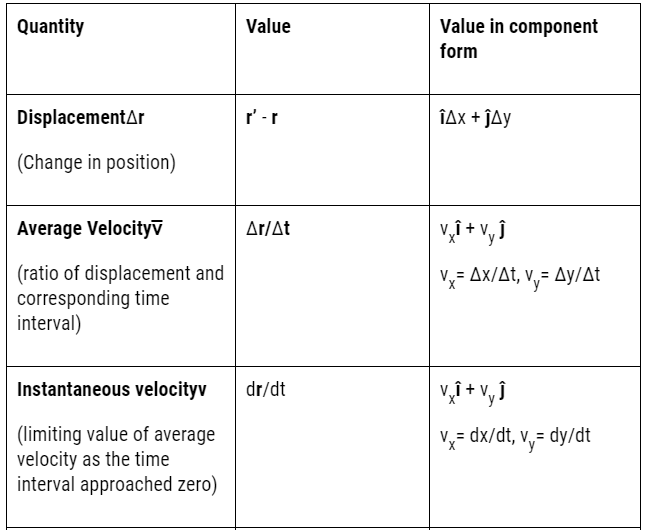
Motion in a plane with constant acceleration

Motion in a plane (two dimensions) can be treated as two separate simultaneous one-dimensional motions with constant acceleration along two perpendicular directions. X and Y directions are hence independent of each other.

If v₀ being the velocity at time 0, the displacement can be written as:

x = x₀ + v_0xt+ ½ a_xt² and y = y₀ + v_0yt+ ½ a_yt²

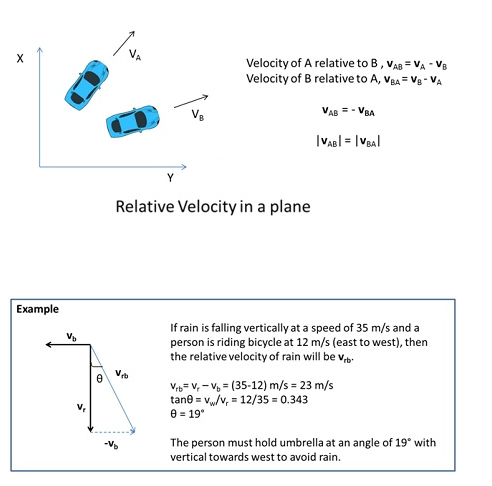
Relative velocity in two dimensions

The concept of relative velocity in a plane is similar to the concept of relative velocity in a straight line.

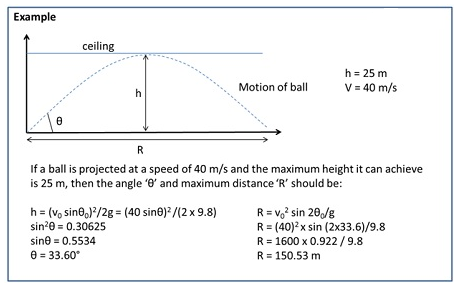
Projectile Motion

An object that becomes airborne after it is thrown or projected is called projectile. Example, football, javelin throw, etc.

Quantity	Value
Components of velocity at time t	vx = v0 cosθ0vy = v0 sinθ0–gt
Position at time t	x = (v0 cosθ0)ty = (v0 sinθ0)t – ½ gt2
Equation of path of projectile motion	y = (tan θ0)x – gx2/2(v0 cosθ0)2
Time of maximum height	tm = v0 sinθ0 /g
Time of flight	2 tm = 2 (v0 sinθ0 /g)
Maximum height of projectile	hm = (v0 sinθ0)2/2g
Horizontal range of projectile	R = v02 sin 2θ0/g
Maximum horizontal range (θ0=45°)	Rm = v02/g

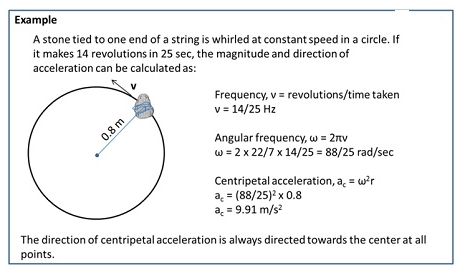
Uniform circular motion

When an object follows a circular path at a constant speed, the motion is called uniform circular motion.

• Velocity at any point is along the tangent at that point in the direction of motion.
• Average velocity between two points is always perpendicular to Average displacement. Also, average acceleration is perpendicular to average displacement.
• For an infinitely small time interval, Δtà 0, the average acceleration becomes instantaneous acceleration which means that in uniform circular motion the acceleration of an object is always directed towards the center. This is called centripetal acceleration.

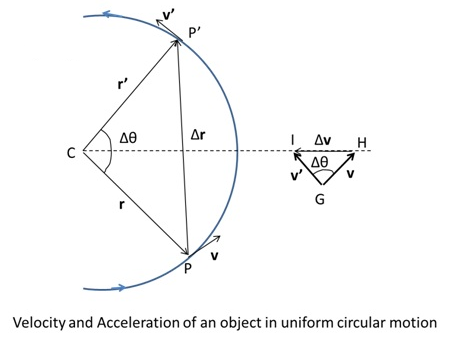
Quantity	Values
Centripetal Acceleration	ac = v2/R, R – radius of the circleac = ω2R, ω – angular speedac = 4π2ν2R, ν – frequency
Angular Distance	Δθ = ω Δt
Speed	v = Rω

Related link you must like:-

HVAC Course

CBSE Study Material

Study material for Competition Exam

Interview Question

Career Option

Spoken English