Exercise 10.1 Page no: 212
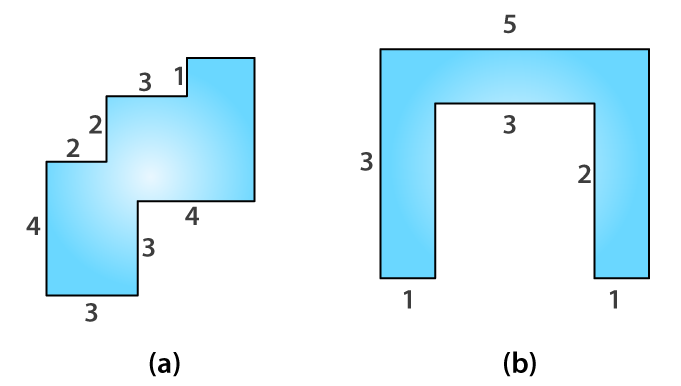
1. Find the perimeter of each of the following figures: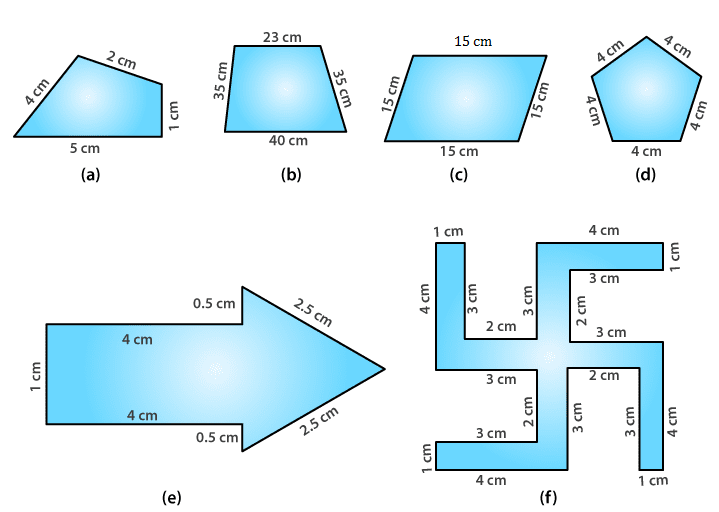
Solutions:
(a) Perimeter = Sum of all the sides
= 1 + 2 + 4 + 5
= 12 cm
(b) Perimeter = Sum of all the sides
= 23 + 35 + 35 + 40
= 133 cm
(c) Perimeter = Sum of all the sides
= 15 + 15 + 15 + 15
= 60 cm
(d) Perimeter = Sum of all the sides
= 4 + 4 + 4 + 4 + 4
=20 cm
(e) Perimeter = Sum of all the sides
= 1 + 4 + 0.5 + 2.5 + 2.5 + 0.5 + 4
= 15 cm
(f) Perimeter = Sum of all the sides
= 4 + 1 + 3 + 2 + 3 + 4 + 1 + 3 + 2 + 3 + 4 + 1 + 3 + 2 + 3 + 4 + 1 + 3 + 2 + 3
= 52 cm
2. The lid of a rectangular box of sides 40 cm by 10 cm is sealed all around with tape. What is the length of the tape required?
Solutions:
Length of required tape = Perimeter of rectangle
= 2 (Length + Breadth)
= 2 (40 + 10)
= 2 (50)
= 100 cm
∴ Required length of tape is 100 cm
3. A table top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the table top?
Solutions:
Length of table top = 2 m 25 cm = 2.25 m
Breadth of table top = 1 m 50 cm = 1.50 m
Perimeter of table top = 2 (Length + Breadth)
= 2 (2.25 + 1.50)
= 2 (3.75)
= 2 × 3.75
= 7.5 m
∴ The perimeter of the table top is 7.5 m
4. What is the length of the wooden strip required to frame a photograph of length and breadth 32 cm and 21 cm respectively?
Solutions:
Required length of wooden strip = Perimeter of photograph
= 2 (Length + Breadth)
= 2 (32 + 21)
= 2 (53)
= 2 × 53
= 106 cm
∴ Required length of the wooden strip is 106 cm
5. A rectangular piece of land measures 0.7 km by 0.5 km. Each side is to be fenced with 4 rows of wires. What is the length of the wire needed?
Solutions:
Perimeter of the field = 2 (Length + Breadth)
= 2 (0.7 + 0.5)
= 2 (1.2)
= 2 × 1.2
= 2.4 km
Each side is to be fenced with 4 rows = 4 × 2.4
= 9.6 km
∴ Total length of the required wire is 9.6 km
6. Find the perimeter of each of the following shapes:
(a) A triangle of sides 3 cm, 4 cm and 5 cm
(b) An equilateral triangle of side 9 cm
(c) An isosceles triangle with equal sides 8 cm each and third side 6 cm.
Solutions:
(a) Perimeter of triangle = 3 + 4 + 5
= 12 cm
(b) Perimeter of an equilateral triangle = 3 × side
= 3 × 9
= 27 cm
(c) Perimeter of isosceles triangle = 8 + 8 + 6
= 22 cm
7. Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.
Solutions:
Perimeter of triangle = 10 + 14 + 15
= 39 cm
∴ The perimeter of triangle is 39 cm
8. Find the perimeter of a regular hexagon with each side measuring 8 m.
Solutions:
Perimeter of hexagon = 6 × 8
= 48 m
∴ Perimeter of regular hexagon is 48 m
9. Find the side of the square whose perimeter is 20 m.
Solutions:
Perimeter of square = 4 × side
20 = 4 × side
Side = 20 / 4
Side = 5 m
∴ The side of the square is 5 m
10. The perimeter of a regular pentagon is 100 cm. How long is its each side?
Solutions:
Perimeter of regular pentagon = 100 cm
5 × side = 100 cm
Side = 100 / 5
Side = 20 cm
∴ Side of the pentagon is 20 cm
11. A piece of strings is 30 cm long. What will be the length of each side if the string is used to form:
(a) a square?
(b) an equilateral triangle?
(c) a regular hexagon?
Solutions:
(a) Perimeter of square = 30 cm
4 × side = 30
Side = 30 / 4
Side = 7.5 cm
(b) Perimeter of an equilateral triangle = 30 cm
3 × side = 30
Side = 30 / 3
Side = 10 cm
(c) Perimeter of a regular hexagon = 30 cm
6 × side = 30
Side = 30 / 6
Side = 5 cm
12. Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
Solutions:
Let x cm be the third side
Perimeter of triangle = 36 cm
12 + 14 + x = 36
26 + x = 36
x = 36 – 26
x = 10 cm
∴ The third side is 10 cm
13. Find the cost of fencing a square park of side 250 m at the rate of ₹ 20 per metre.
Solutions:
Side of square = 250 m
Perimeter of square = 4 × side
= 4 × 250
= 1000 m
Cost of fencing = ₹ 20 per m
Cost of fencing for 1000 m = ₹ 20 × 1000
= ₹ 20,000
14. Find the cost of fencing a rectangular park of length 175 cm and breadth 125 m at the rate of ₹ 12 per metre.
Solutions:
Length = 175 cm
Breadth = 125 m
Perimeter of rectangular park = 2 (Length + Breadth)
= 2 (175 + 125)
= 2 (300)
= 2 × 300
= 600 m
Cost of fencing = 12 × 600
= 7200
∴ Cost of fencing is ₹ 7,200
15. Sweety runs around a square park of side 75 m. Bulbul runs around a rectangular park with length 60 m and breadth 45 m. Who covers less distance?
Solutions:
Perimeter of square = 4 × side
= 4 × 75
= 300 m
∴ Distance covered by Sweety is 300 m
Perimeter of rectangular park = 2 (Length + Breadth)
= 2 (60 + 45)
= 2 (105)
= 2 × 105
= 210 m
∴ Distance covered by Bulbul is 210 m
Hence, Bulbul covers less distance than Sweety.
16. What is the perimeter of each of the each of the following figures? What do you infer from the the answers?
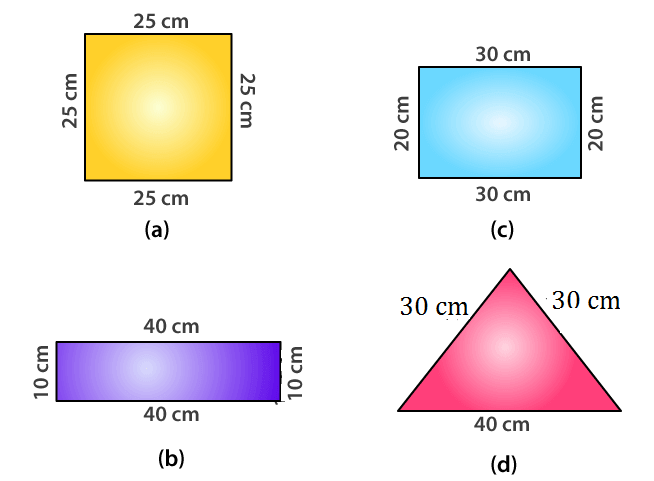
Solutions:
(a) Perimeter of square = 4 × side
= 4 × 25
= 100 cm
(b) Perimeter of rectangle = 2 (40 + 10)
= 2 × 50
= 100 cm
(c) Perimeter of rectangle = 2 (Length + Breadth)
= 2 (30 + 20)
= 2 (50)
= 2 × 50
= 100 cm
(d) Perimeter of triangle = 30 + 30 + 40
= 100 cm
All the figures have same perimeter.
17. Avneet buys 9 square paving slabs, each with a side of 1 / 2 m. He lays them in the form of a square.
(a) What is the perimeter of his arrangement [fig 10.7(i)]?
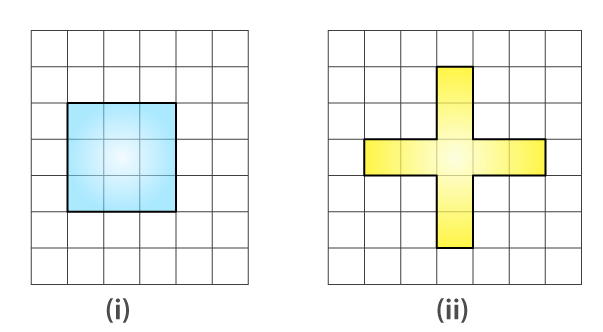
(b) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement [(Fig 10.7 (ii)]?
(c) Which has greater perimeter?
(d) Avneet wonders if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges i.e they cannot be broken.)
Solutions:
(a) Side of square = 3 × side
= 3 × 1 / 2
= 3 / 2 m
Perimeter of Square = 4 × 3 / 2
= 2 × 3
= 6 m
(b) Perimeter = 0.5 + 1 + 1 + 0.5 + 1 + 1 + 0.5 + 1 + 1 + 0.5 + 1 + 1
= 10 m
(c) The arrangement in the form of cross has greater perimeter
(d) Perimeters greater than 10 m cannot be determined.
Exercise 10.2 page no: 216
1. Find the areas of the following figures by counting square: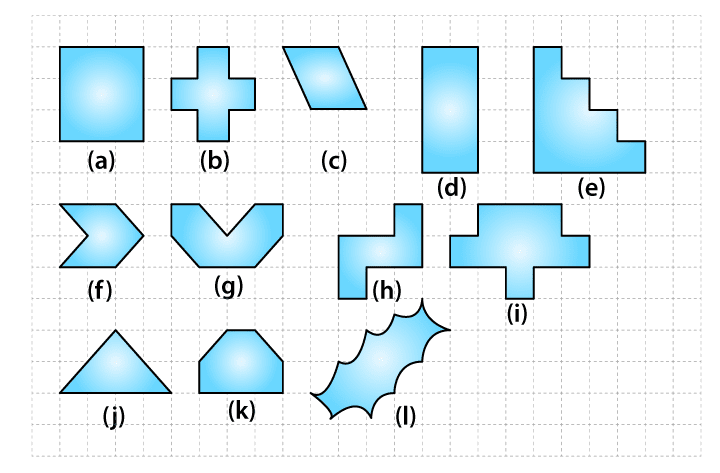

(a) The figure contains only 9 fully filled squares. Hence, the area of this figure will be 9 square units.
(b) The figure contains only 5 fully filled squares. Hence, the area of this figure will be 5 square units.
(c) The figure contains 2 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 4 square units.
(d) The figure contains only 8 fully filled squares. Hence, the area of this figure will be 8 square units.
(e) The figure contains only 10 fully filled squares. Hence, the area of this figure will be 10 square units.
(f) The figure contains only 2 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 4 square units.
(g) The figure contains 4 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 6 square units.
(h) The figure contains 5 fully filled squares. Hence, the area of this figure will be 5 square units.
(i) The figure contains 9 fully filled squares. Hence, the area of this figure will be 9 square units.
(j) The figure contains 2 fully filled squares and 4 half filled squares. Hence, the area of this figure will be 4 square units.
(k) The figure contains 4 fully filled squares and 2 half filled squares. Hence, the area of this figure will be 5 square units.
(l) From the given figure, we observe
| Covered Area | Number | Area estimate (square units) |
| Fully filled squares | 2 | 2 |
| Half filled squares | – | – |
| More than half filled squares | 6 | 6 |
| Less than half filled squares | 6 | 0 |
Therefore total area = 2 + 6
= 8 square units.
(m) From the given figure, we observe
| Covered Area | Number | Area estimate (square units) |
| Fully filled squares | 5 | 5 |
| Half filled squares | – | – |
| More than half filled squares | 9 | 9 |
| Less than half filled squares | 12 | 0 |
Therefore total area = 5 + 9
= 14 square units
(n) From the given figure, we observe
| Covered Area | Number | Area estimate (square units) |
| Fully filled squares | 8 | 8 |
| Half filled squares | – | – |
| More than half filled squares | 10 | 10 |
| Less than half filled squares | 9 | 0 |
Therefore total area = 8 + 10 = 18 square units
Exercise 10.3 page no: 219
1. Find the area of the rectangles whose sides are:
(a) 3 cm and 4 cm
(b) 12 m and 21 m
(c) 2 km and 3 km
(d) 2 m and 70 cm
Solutions:
We know that
Area of rectangle = Length × Breadth
(a) l = 3 cm and b = 4 cm
Area = l × b = 3 × 4
= 12 cm2
(b) l = 12 m and b = 21 m
Area = l × b = 12 × 21
= 252 m2
(c) l = 2 km and b = 3 km
Area = l × b = 2 × 3
= 6 km2
(d) l = 2 m and b = 70 cm = 0.70 m
Area = l × b = 2 × 0.70
= 1.40 m2
2. Find the areas of the squares whose sides are:
(a) 10 cm
(b) 14 cm
(c) 5 m
Solutions:
(a) Area of square = side2
= 102
= 100 cm2
(b) Area of square = side2
= 142
= 196 cm2
(c) Area of square = side2
= 52
=25 cm2
3. The length and breadth of three rectangles are as given below:
(a) 9 m and 6 m
(b) 17 m and 3 m
(c) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Solutions:
(a) Area of rectangle = l × b
= 9 × 6
= 54 m2
(b) Area of rectangle = l × b
= 17 × 3
= 51 m2
(c) Area of rectangle = l × b
= 4 × 14
= 56 m2
Area of rectangle 56 m2 i.e (c) is the largest area and area of rectangle 51 m2 i.e (b) is the smallest area
4. The area of a rectangular garden 50 m long is 300 sq m. Find the width of the garden.
Solutions:
Area of rectangle = length × width
300 = 50 × width
width = 300 / 50
width = 6 m
∴ The width of the garden is 6 m
5. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m.?
Solutions:
Area of land = length × breadth
= 500 × 200
= 1,00,000 m2
∴ Cost of tiling 1,00,000 sq m of land = (8 × 1,00,000) / 100
= ₹ 8000
6. A table top measures 2 m by 1 m 50 cm. What is its area in square metres?
Solutions:
Given
l = 2m
b = 1m 50 cm = 1.50 m
Area = l × b = 2 × 1.50
= 3 m2
7. A room is 4 m long and 3 m 50 cm wide. Howe many square metres of carpet is needed to cover the floor of the room?
Solutions:
Given
l = 4m
b = 3 m 50 cm = 3.50 m
Area = l × b = 4 × 3.50
=14 m2
8. A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solutions:
Area of floor = l × b = 5 × 4
= 20 m2
Area of square carpet = 3 × 3
= 9 m2
Area of floor that is not carpeted = 20 – 9
= 11 m2
∴ Area of the floor that is not carpeted is 11 m2
9. Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
Solutions:
Area of flower square bed = 1 × 1
= 1 m2
Area of 5 square bed = 1 × 5
= 5 m2
Area of land = 5 × 4
= 20 m2
Remaining part of the land = Area of land – Area of 5 square bed
= 20 – 5
= 15 m2
∴ Remaining part of the land is 15 m2
10. By splitting the following figures into rectangles, find their areas (The measures are given in centimetres).
Solutions:
(a)
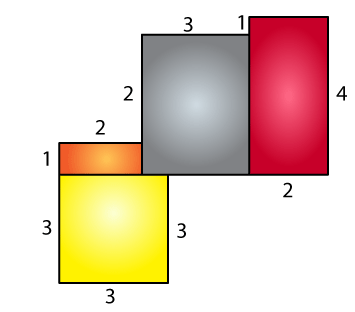
Area of yellow region = 3 × 3
= 9 cm2
Area of orange region = 1× 2
= 2 cm2
Area of grey region = 3 × 3
= 9 cm2
Area of brown region = 2 × 4
= 8 cm2
Total area = 9 + 2 + 9 + 8
= 28 cm2
∴ Total area is 28 cm2
(b)
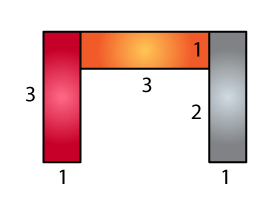
Area of brown region = 3 × 1
= 3 cm2
Area of orange region = 3 × 1
= 3 cm2
Area of grey region = 3 × 1
= 3 cm2
Total area = 3 + 3 + 3
= 9 cm2
∴ Total area is 9 cm2
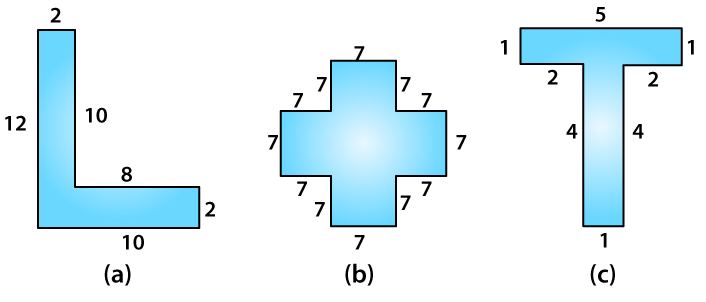
11. Split the following shapes into rectangles and find their areas. (The measures are given in centimetres)
Solutions:
(a)
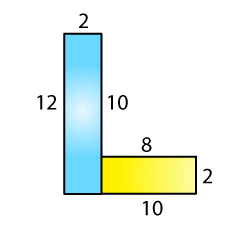
Total area of the figure = 12 × 2 + 8 × 2
= 40 cm2
(b)

There are 5 squares. Each side is 7 cm
Area of 5 squares = 5 × 72
= 245 cm2
(c)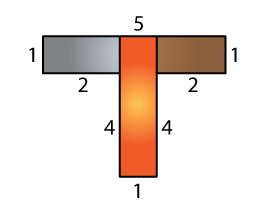
Area of grey rectangle = 2 × 1
= 2 cm2
Area of brown rectangle = 2 × 1
= 2 cm2
Area of orange rectangle = 5 × 1
= 5 cm2
Total area = 2 + 2 + 5
= 9 cm2
12. How many tiles whose length and breadth are 12 cm and 5 cm, respectively will be needed to fit in a rectangular region whose length and breadth are respectively?
(a) 100 cm and 144 cm
(b) 70 cm and 36 cm
Solutions:
(a) Area of rectangle = 100 × 144
= 14400 cm
Area of one tile = 5 × 12
= 60 cm2
Number of tiles = (Area of rectangle) / (Area of one tile)
= 14400 / 60
= 240
Hence, 240 tiles are needed
(b) Area of rectangle = 70 × 36
= 2520 cm2
Area of one tile = 5 × 12
= 60 cm2
Number of tiles = (Area of rectangle) / (Area of one tile)
= 2520 / 60
= 42
Hence, 42 tiles are needed.