Class 6 Chapter 14: Practical Geometry
Exercise 14.1 page no: 276
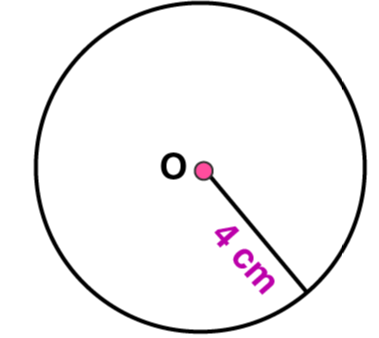
1. Draw a circle of radius 3.2 cm.
Solutions:
The required circle may be drawn as follows:
Step 1: For the required radius 3.2 cm, first open the compasses.
Step 2: For the centre of a circle, mark a point ‘O’.
Step 3: Place a pointer of compasses on ‘O’.
Step 4: Now, turn the compasses slowly to draw the required circle.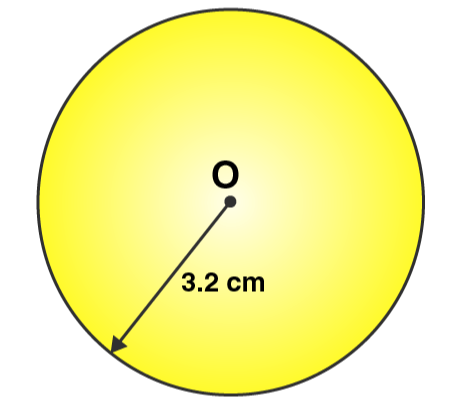
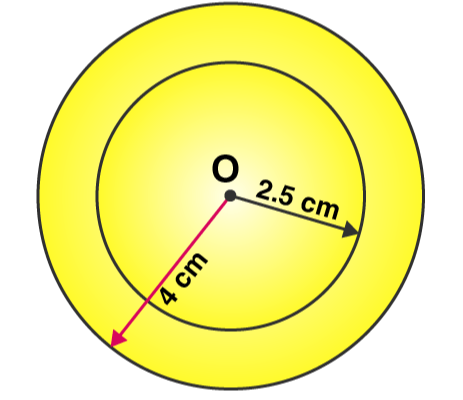
2. With the same centre O, draw two circles of radii 4 cm and 2.5 cm.
Solutions:
The required circle may be drawn as follows:
Step 1: For the required radius 4 cm, first open the compasses
Step 2: For the centre of a circle, mark a point ‘O’
Step 3: Place a pointer of compasses on ‘O’.
Step 4: Turn the compasses slowly to draw the circle.
Step 5: Next, open the compasses for 2.5 cm.
Step 6: Again place a pointer of compasses on ‘O’ and turn the compasses slowly to draw the circle.
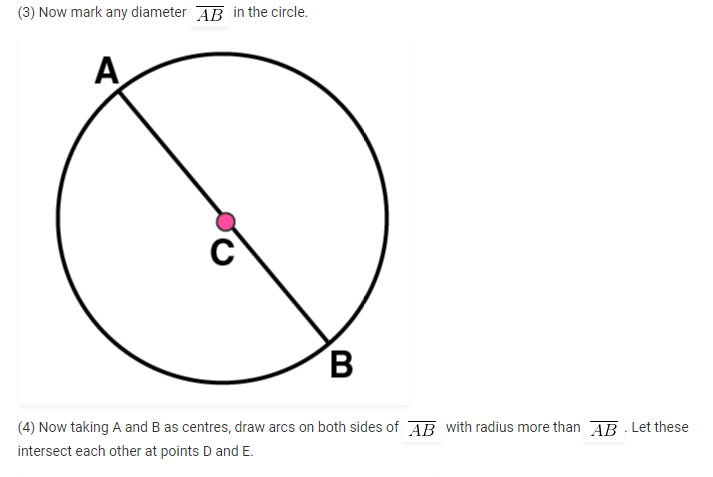
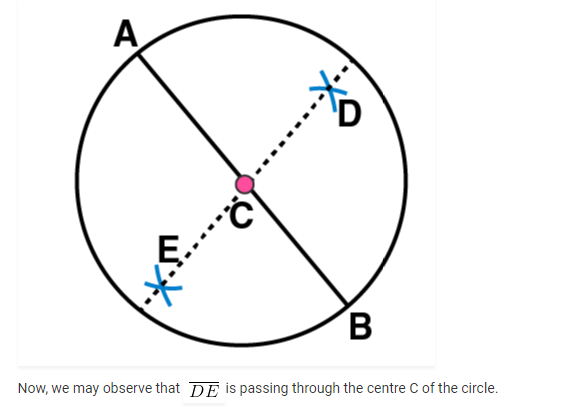
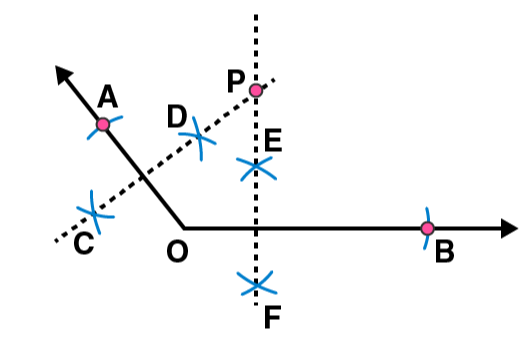
3. Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained? What figure is obtained if the diameters are perpendicular to each other? How do you check your answer?
Solutions:
We may draw a circle having its centre ‘O’, also of any convenient radius. Let AB and CD be the two diameters of this circle. A quadrilateral is formed when we join the ends of these diameters.
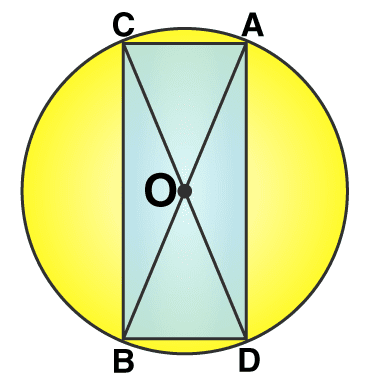
We know that the diameter of a circle are equal in length, hence quadrilateral formed will be having its diagonals of equal length.
Also, OA = OB = OC = OD = radius r and if a quadrilateral has its diagonals of same length bisecting each other. It will be a rectangle.
Let DE and FG be the diameters of the circle such that both are perpendicular to each other. Now we can find that a quadrilateral is formed by joining the ends of these diameters.
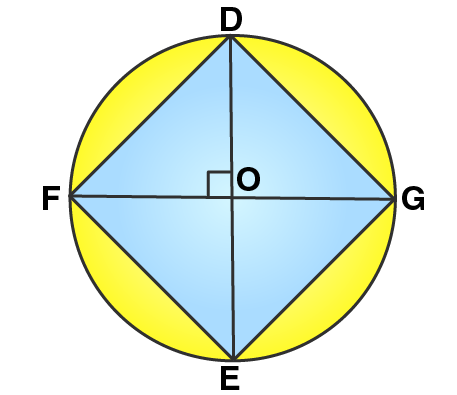
We may find that OD = OE = OF = OG = radius r.
In this quadrilateral DFEG, diagonals are equal and perpendicular to each other. Also they are bisecting each other, hence it will be a square.
To check our answers we may measure the length of sides of quadrilateral formed.
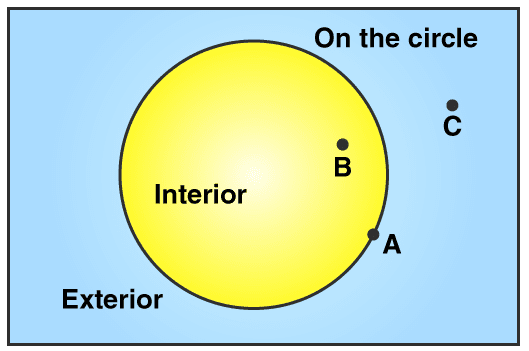
4. Draw any circle and mark points A, B and C such that
(a) A is on the circle.
(b) B is in the interior of the circle.
(c) C is in the exterior of the circle.
Solutions:
We may draw a circle and three required points A, B, C as follows:

Exercise 14.2 Page no: 278
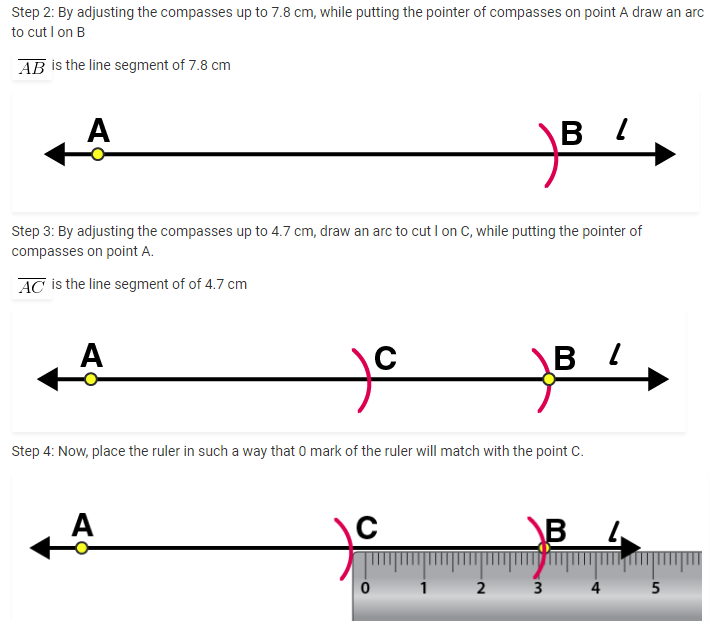
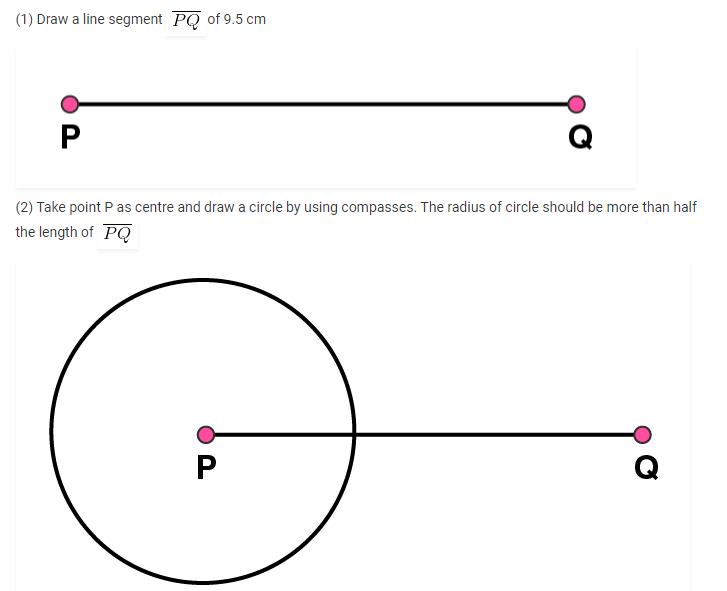
1. Draw a line segment of length 7.3 cm using a ruler.
Solutions:
Using a ruler, we can draw a line segment of length 7.3 cm as follows
Step 1: Mark a point A on the sheet
Step 2: Place 0 mark of ruler at point A
Step 3: At 7.3 cm on ruler, mark a point B on the sheet





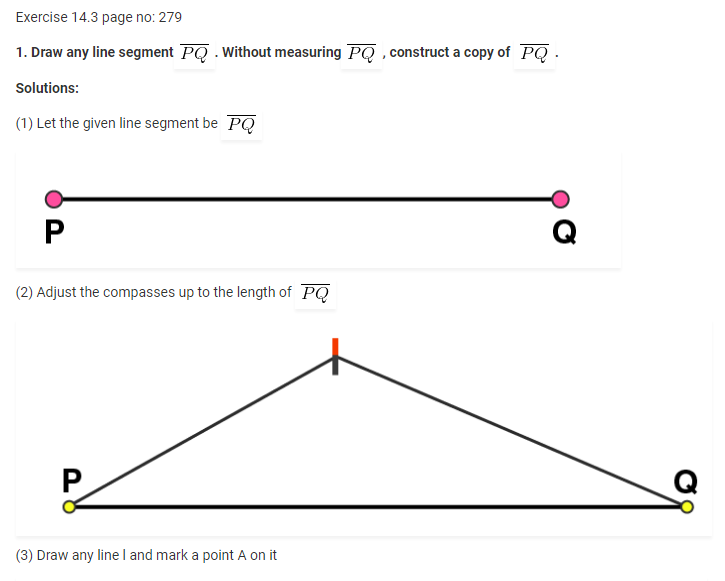


Exercise 14.4 Page no: 284

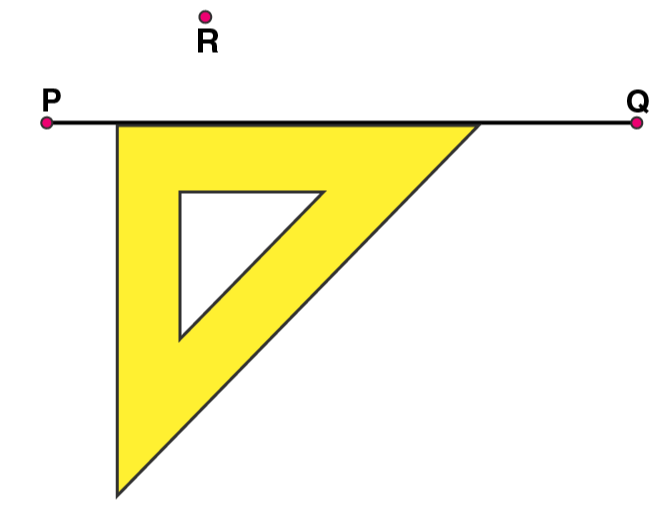
(3) Now, place the ruler along the edge opposite to right angle of set square.
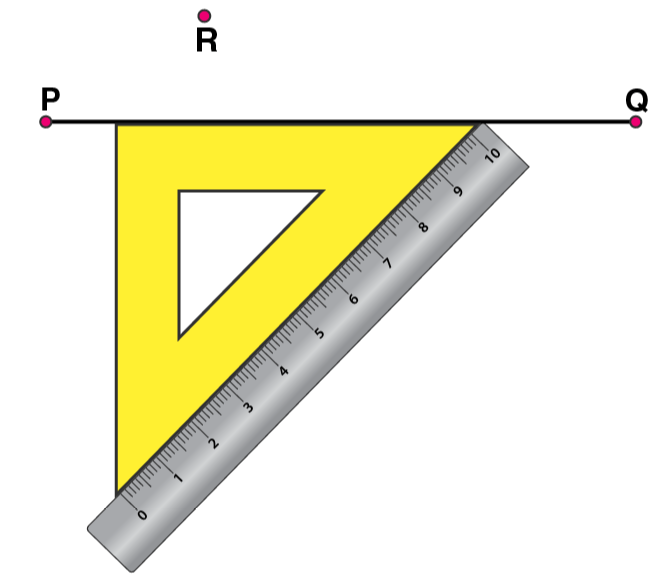
(4) Hold the ruler fixed. Slide the set square along the ruler such that the point R touches the other arm of set square.
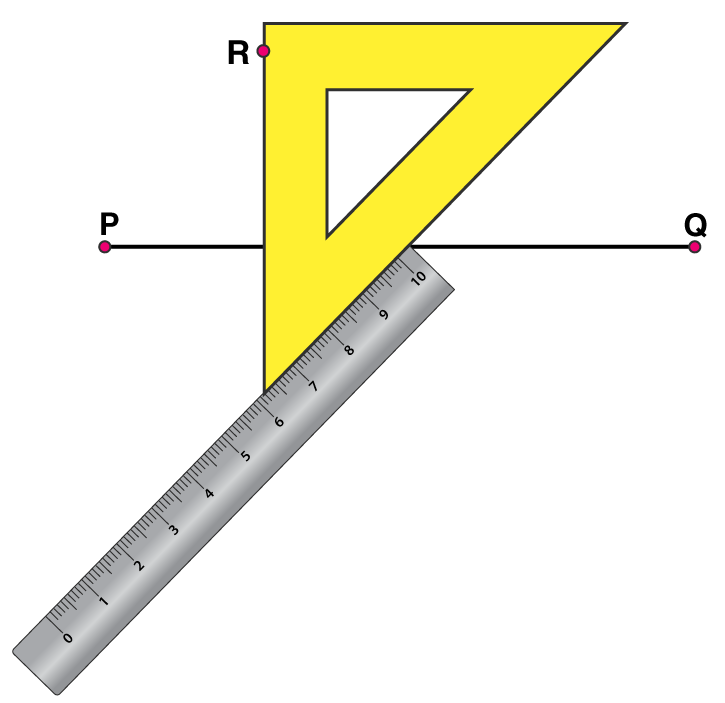

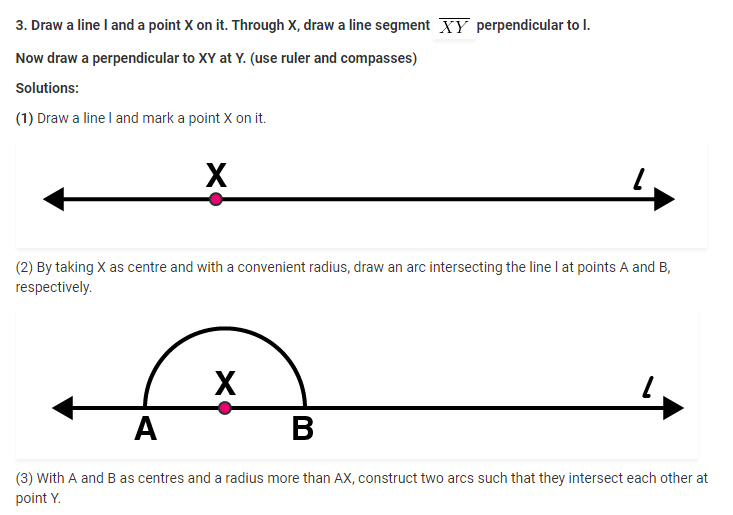
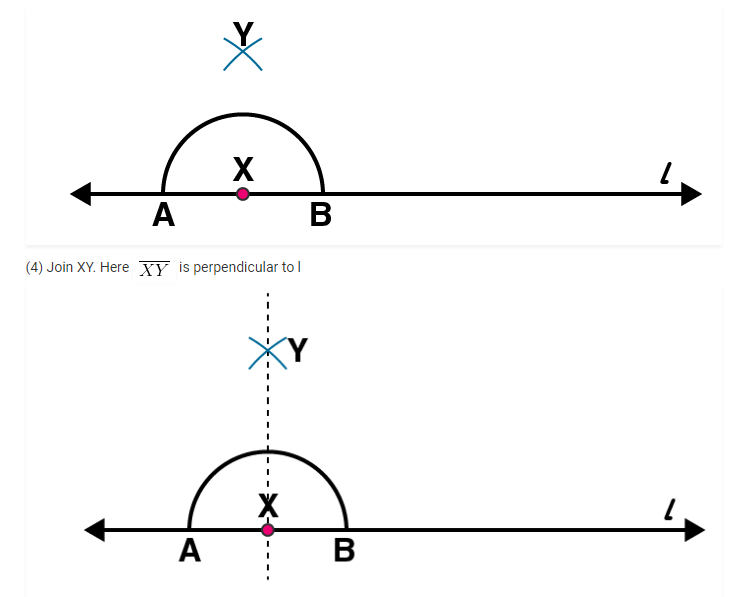

Exercise 14.5 page no: 286


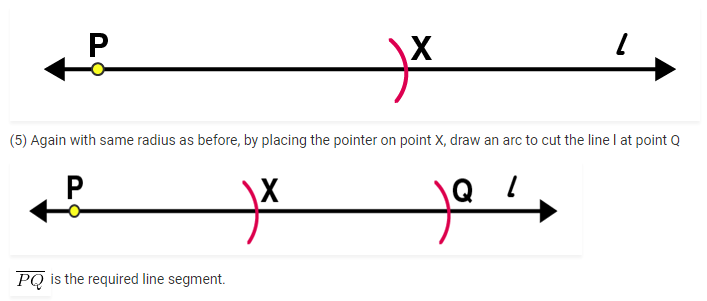
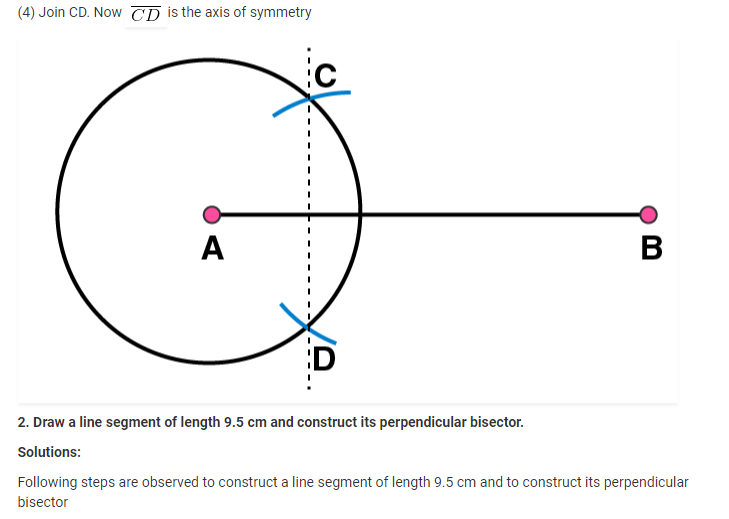
(3) Now, take B as centre and draw another circle using compasses with the same radius as before. Let it cut the previous circle at points C and D

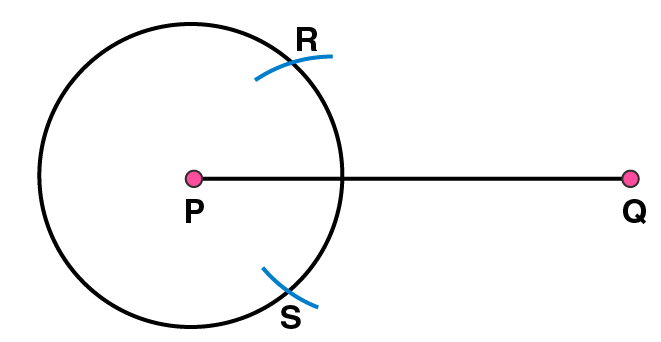
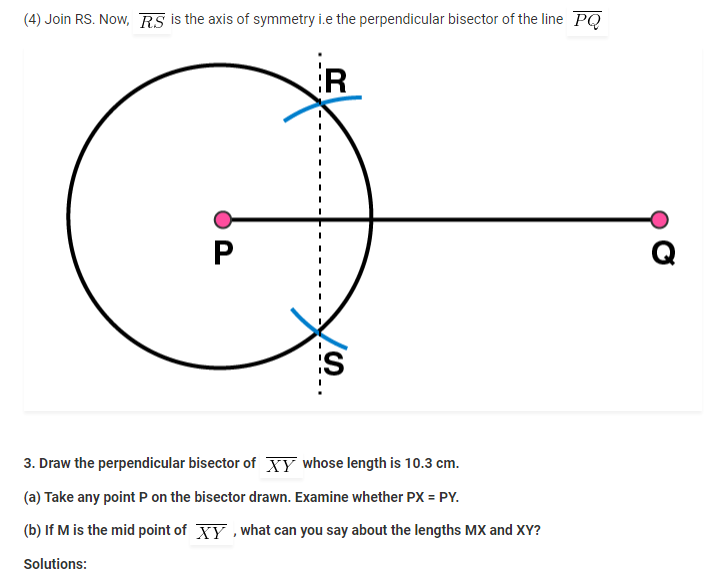
(3) Taking the centre at point Q, again draw another circle using compasses with the same radius as before. Let it cut the previous circle at R and S respectively.
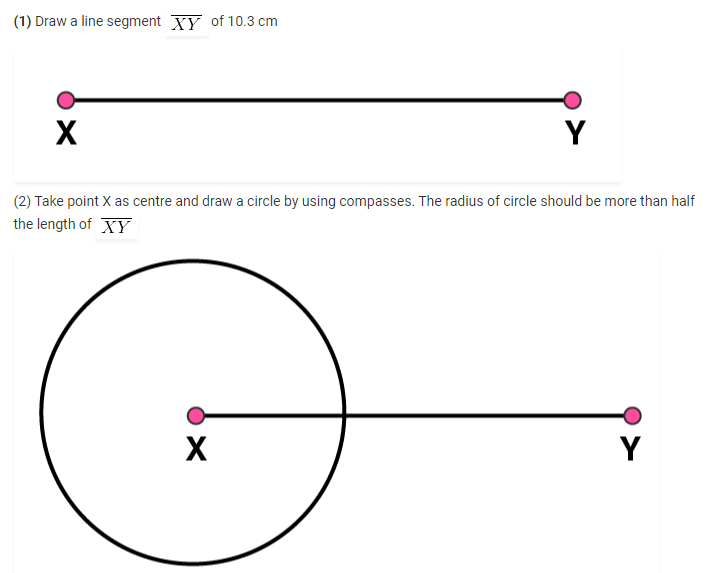
(3) Now taking Y as centre, draw another circle using compasses with the same radius as before. Let it cut at previous circle at points A and B
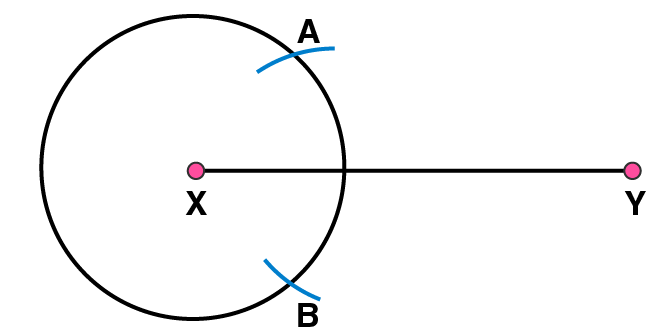
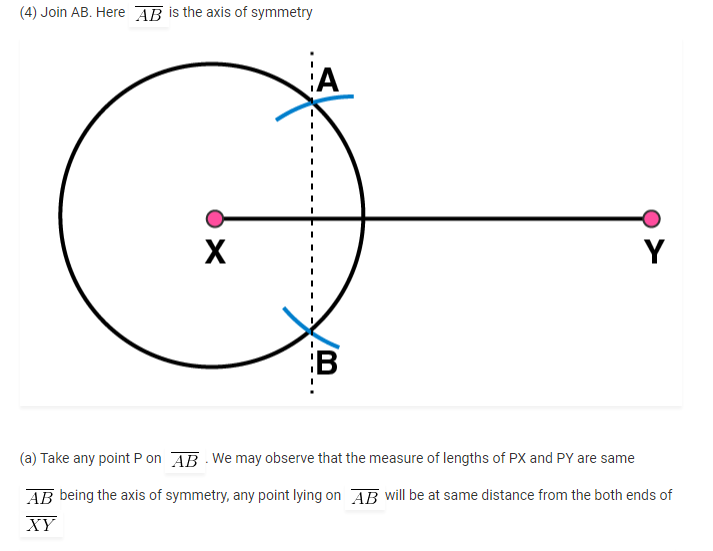
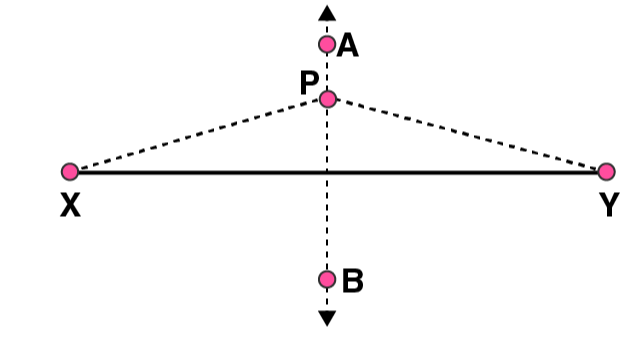

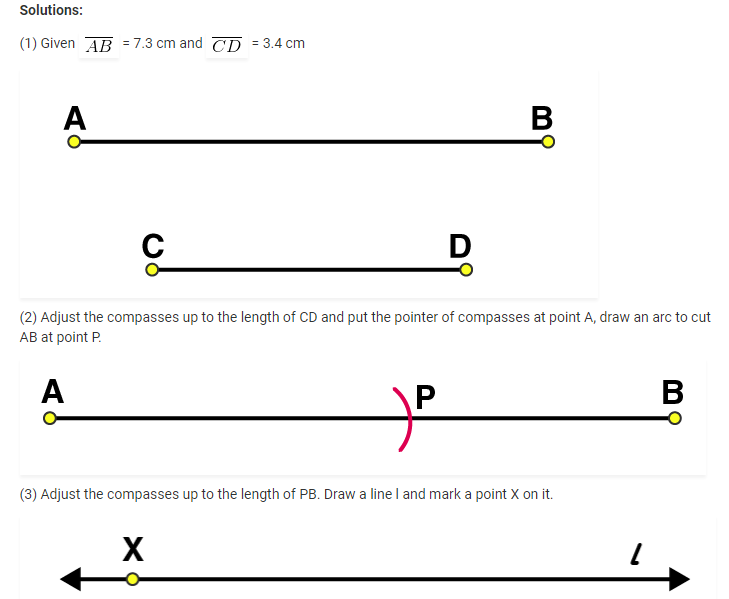
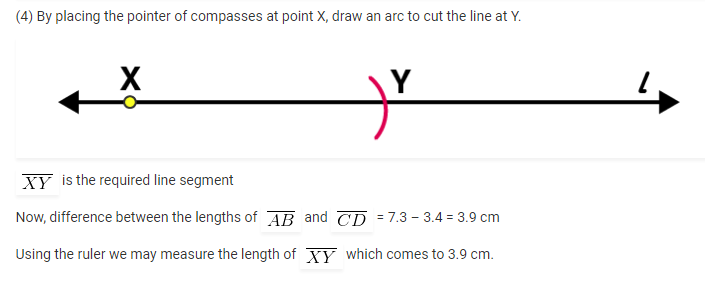
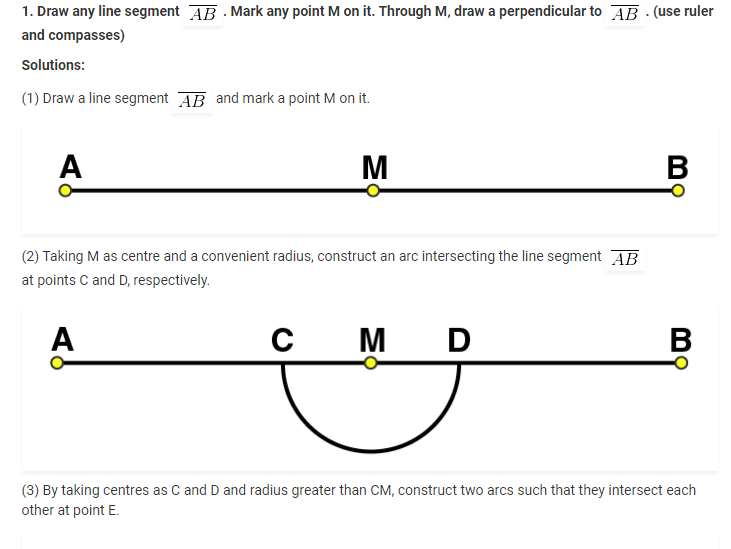
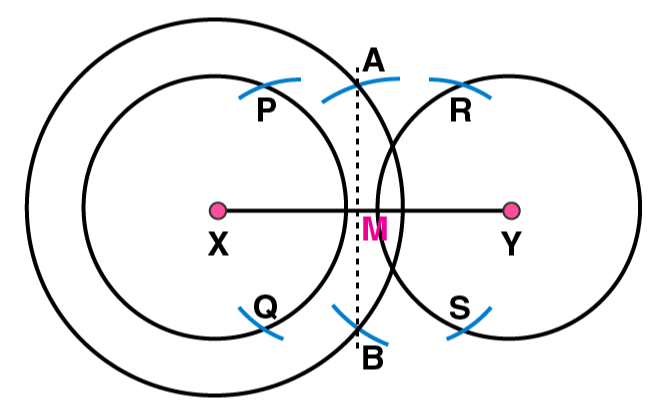
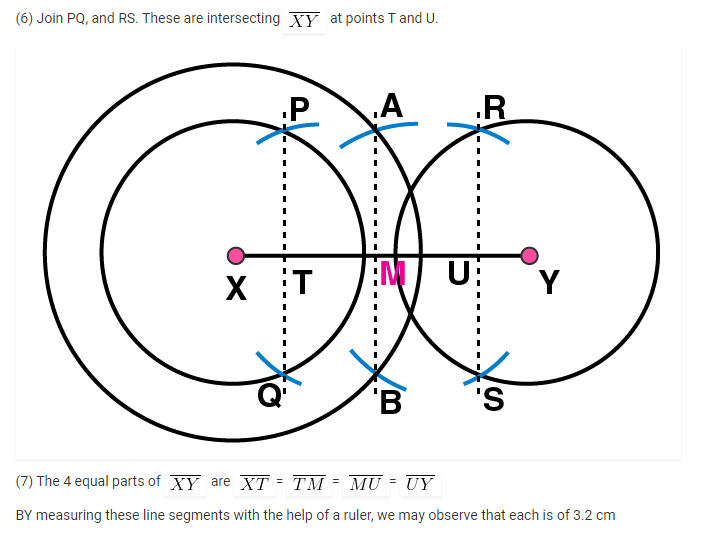
4. Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
Solutions:

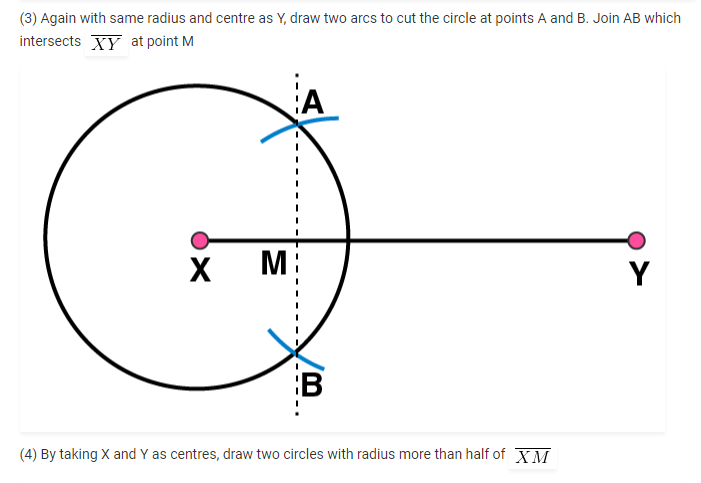
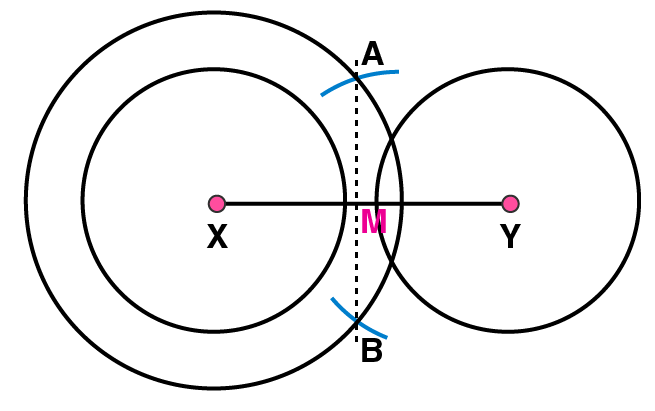
(5) Taking M as centre and with same radius, draw two arcs to intersect these circles at P, Q and R, S
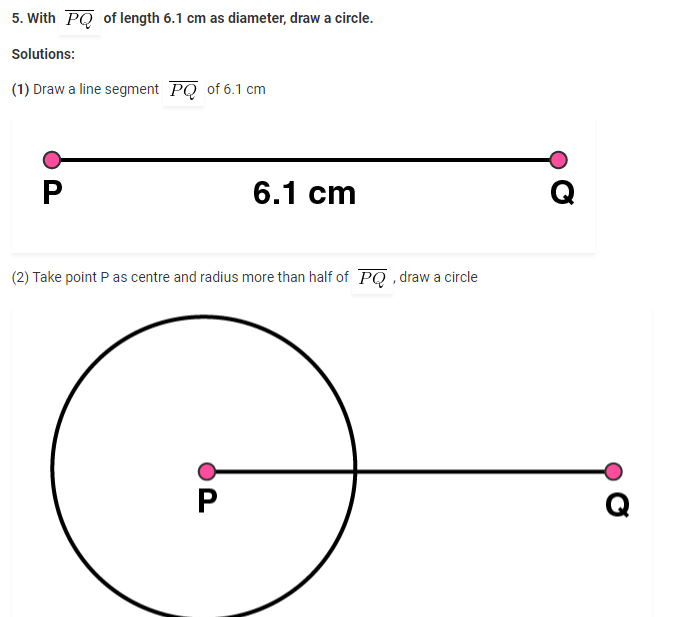
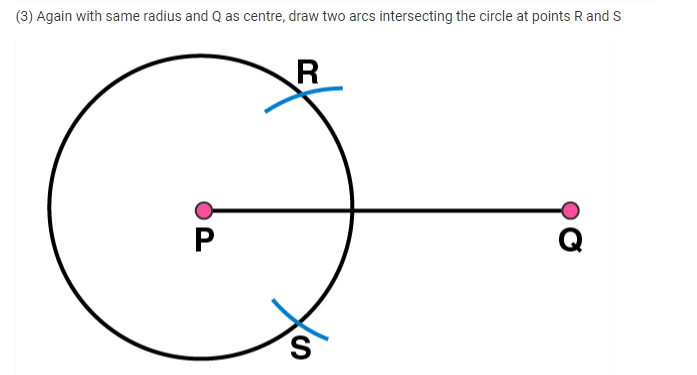

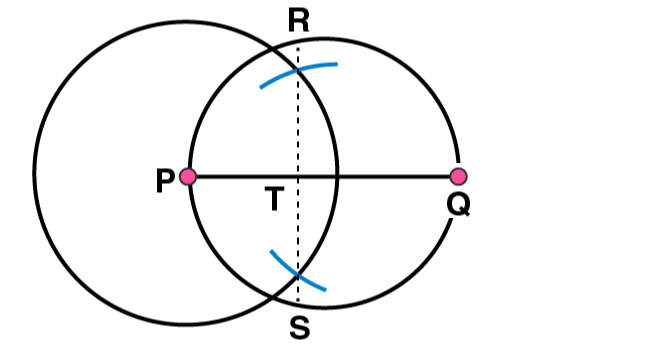
(5) Taking the centre as T and radius TP, draw a circle which passes through Q. Now, this is the required circle.

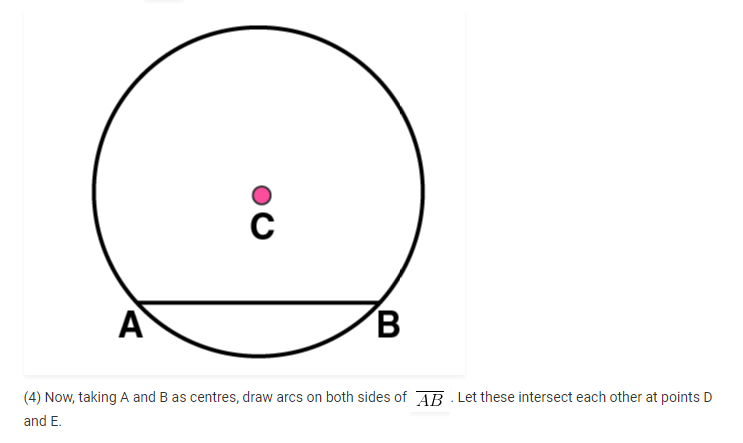
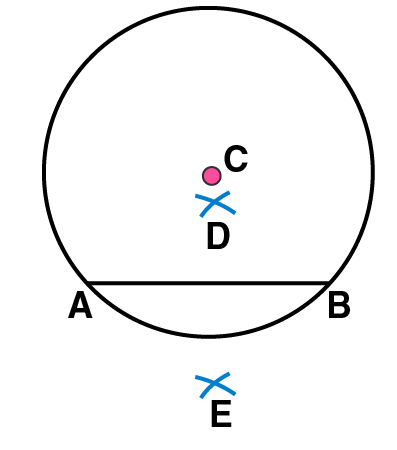
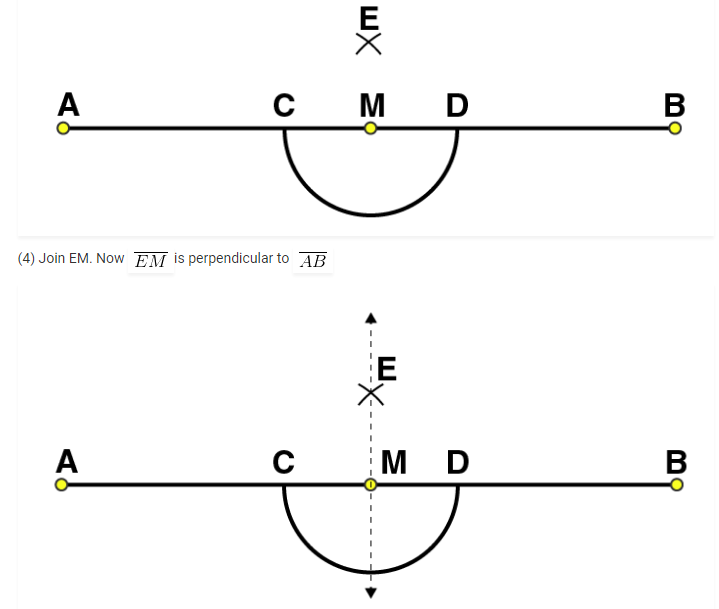
(5) Join DE. Now DE is the perpendicular bisector of AB.

(1) Mark any point C on the sheet.
(2) Adjust the compasses up to 3.4 cm and by putting the pointer of compasses at point C, Turn the compasses slowly to draw the circle. This is the required circle of 3.4 cm


8. Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
Solutions:
(1) Mark any point O on the sheet. Now adjust the compasses up to 4 cm and by placing the pointer of compasses at point O, turn the compasses slowly to draw the circle. This is the required circle of 4 cm radius

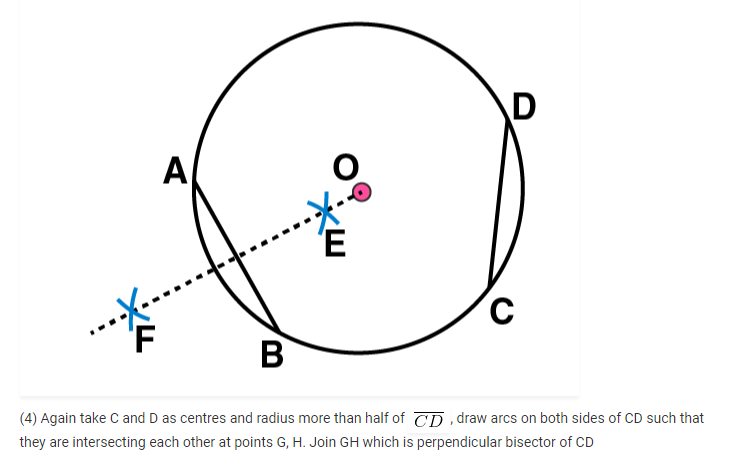
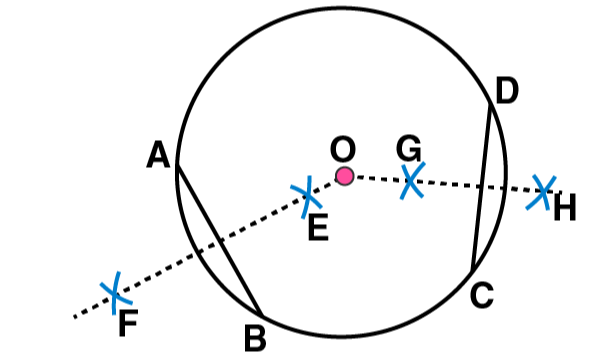
We may observe that when EF and GH are extended they meet at the point O, which is the centre of circle


(3) Now take O and A as centres and with radius more than half of OA, draw arcs on both sides of OA. Let these intersects at points C and D respectively. Join CD

Exercise 14.6 page no: 291
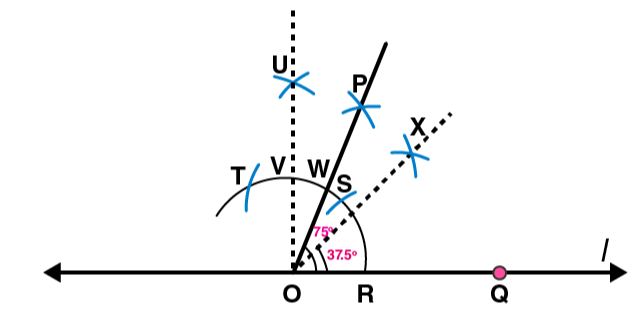
1. Draw ∠POQ of measure 75° and find its line of symmetry.
Solutions:
Following steps are followed to construct an angle of 750 and its line of symmetry
(i) Draw a line l and mark two points O and Q on it. Draw an arc of convenient radius, while taking centre as O. Let this intersect line l at R
(ii) Taking R as centre and with same radius as before, draw an arc such that it is intersecting the previously drawn arc at S
(iii) By taking same radius as before and S as centre, draw an arc intersecting the arc at point T as shown in figure
(iv) Take S and T as centre, draw an arc of same radius such that they intersect each other at U
(v) Join OU. Let it intersect the arc at V. Now, take S and V as centres draw arcs with radius more than 1 / 2 SV. Let these intersect each other at P. Join OP. Now OP is the ray making 750 with the line l.
(vi) Let this ray intersect our major arc at point W. By taking R and W as centres, draw arcs with radius more than 1 / 2 RW in the interior angle of 750. Let these intersect each other at point X. Join OX
OX is the line of symmetry for the ∠POQ = 750
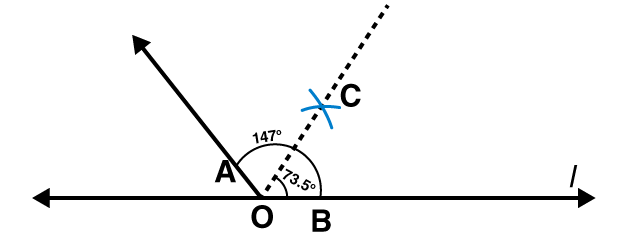
2. Draw an angle of measure 147° and construct its bisector.
Solutions:
Following steps are followed to construct an angle of measure 1470 and its bisector
(i) Draw a line l and mark point O on it. Place the centre of protractor at point O and the zero edge along line l
(ii) Mark a point A at an angle of measure 1470. Join OA. Now OA is the required ray making 1470 with line l
(iii) By taking point O as centre, draw an arc of convenient radius. Let this intersect both rays of angle 1470 at points A and B.
(iv) By taking A and B as centres draw arcs of radius more than 1 / 2 AB in the interior angle of 1470. Let these intersect each other at point C. Join OC.
OC is the required bisector of 1470 angle
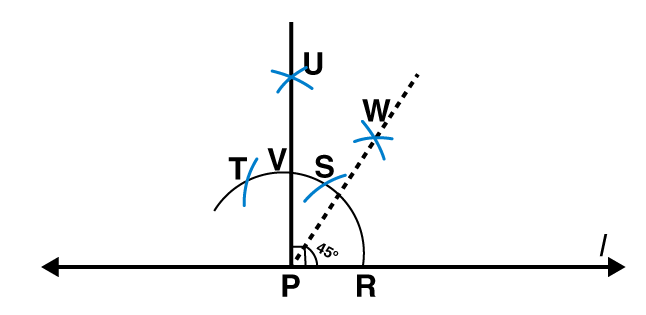
3. Draw a right angle and construct its bisector.
Solutions:
Following steps are followed to construct a right angle and its bisector.
(i) Draw a line l and mark a point P on it. Draw an arc of convenient radius by taking point P as centre. Let this intersect line l at R
(ii) Draw an arc by taking R as centre and with the same radius as before such that it is intersecting the previously drawn arc at S
(iii) Take S as centre and with the same radius as before, draw an arc intersecting the arc at T as shown in figure
(iv) By taking S and T as centres draw arcs of same radius such that they are intersecting each other at U.
(v) Join PU. PU is the required ray making a right angle with the line l. Let this intersect major arc at point V.
(vi) Now take R and V as centres, draw arcs with radius more than 1 / 2 RV to intersect each other at point W. Join PW.
PW is the required bisector of this right angle.
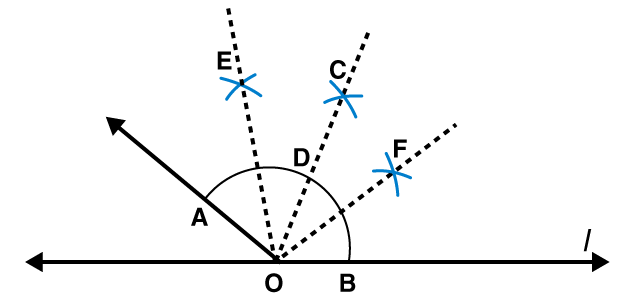
4. Draw an angle of measure 153° and divide it into four equal parts.
Solutions:
Following steps are followed to construct an angle of measure 1530 and its bisector
(i) Draw a line l and mark a point O on it. Place the centre of protractor at point O and the zero edge along line l
(ii) Mark a point A at the measure of angle 1530. Join OA. Now OA is the required ray making 1530 with line l
(iii) Draw an arc of convenient radius by taking point O as centre. Let this intersects both rays of angle 1530 at points A and B.
(iv) Take A and B as centres and draw arcs of radius more than 1 / 2 AB in the interior of angle of 1530. Let these intersect each other at C. Join OC
(v) Let OC intersect major arc at point D. Draw arcs of radius more than 1 / 2 AD with A and D as centres and also D and B as centres. Let these are intersecting each other at points E and F respectively. Now join OE and OF
OF, OC, OE are the rays dividing 1530 angle into four equal parts.
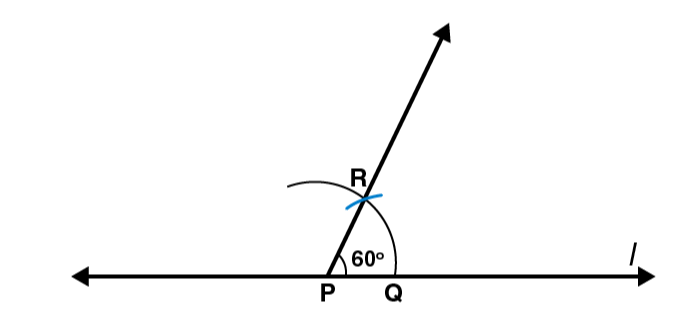
5. Construct with ruler and compasses, angles of following measures:
(a) 60°
(b) 30°
(c) 90°
(d) 120°
(e) 45°
(f) 135°
Solutions:
(a) 600
Following steps are followed to construct an angle of 600
(i) Draw a line l and mark a point P on it. Take P as centre and with convenient radius, draw an arc of a circle such that it intersects the line l at Q.
(ii) Take Q as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at point R.
(iii) Join PR. PR is the required ray making 600 with the line l.
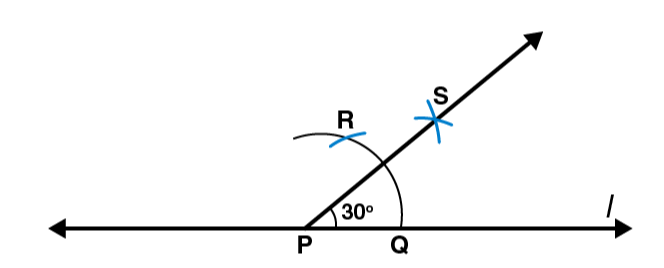
(b) 300
Following steps are followed to construct an angle of 300
(i) Draw a line l and mark a point P on it. By taking P as centre and with convenient radius, draw an arc of a circle such that it is intersecting the line l at Q.
(ii) Take Q as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at point R.
(iii) By taking Q and R as centres and with radius more than 1 / 2 RQ draw arcs such that they are intersecting each other at S. Join PS which is the required ray making 300 with the line l.
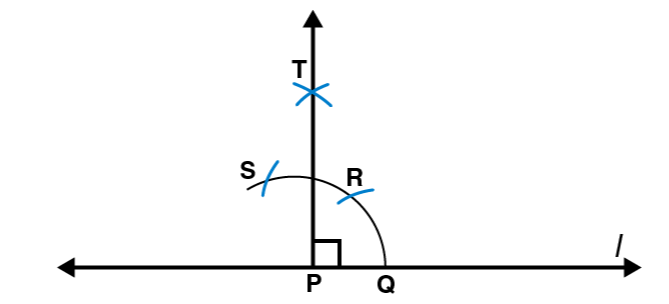
(c) 900
Following steps are followed to construct an angle of measure 900
(i) Draw a line l and mark a point P on it. Take P as centre and with convenient radius, draw an arc of a circle such that it is intersecting the line l at Q.
(ii) Take Q as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at R
(iii) By taking R as centre and with the same radius as before, draw an arc intersecting the arc at S as shown in figure
(iv) Now take R and S as centre, draw arc of same radius to intersect each other at T.
(v) Join PT, which is the required ray making 900 with the line l.
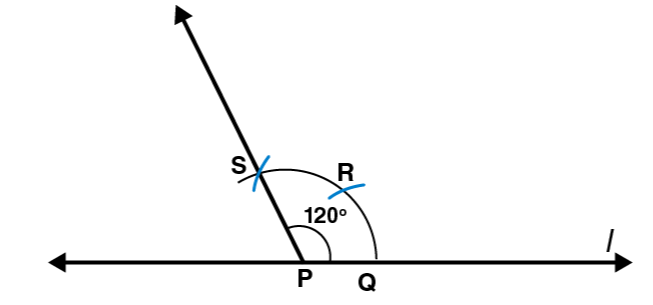
(d) 1200
Following steps are followed to construct an angle of measure 1200
(i) Draw a line l and mark a point P on it. Taking P as centre and with convenient radius, draw an arc of circle such that it is intersecting the line l at Q.
(ii) By taking Q as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at R.
(iii) Take R as centre and with the same radius as before, draw an arc such that it is intersecting the arc at S as shown in figure.
(iv) Join PS, which is the required ray making 1200 with the line l
(e) 450
Following steps are followed to construct an angle of measure 450
(i) Draw a line l and mark a point P on it. Take P as centre and with convenient radius, draw an arc of a circle such that it is intersecting the line l at Q.
(ii) Take Q as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at R
(iii) By taking R as centre and with the same radius as before, draw an arc such that it is intersecting the arc at S as shown in figure.
(iv) Take R and S as centres and draw arcs of same radius such that they are intersecting each other at T
(v) Join PT. Let this intersect the major arc at point U.
(vi) Now take Q and U as centres and draw arcs with radius more than 1 / 2 QU to intersect each other at point V. Join PV.
PV is the required ray making 450 with the line l

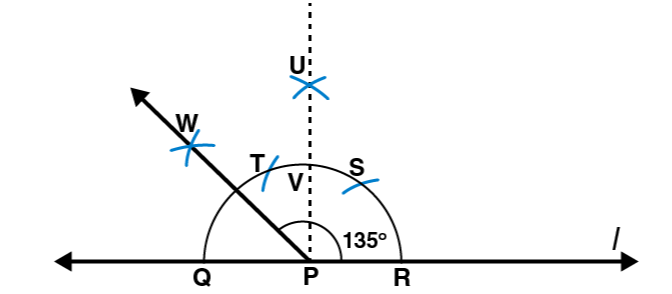
(f) 1350
Following steps are followed to construct an angle of measure 1350
(i) Draw a line l and mark a point P on it. Taking P as centre and with convenient radius, draw a semicircle which intersects the line l at Q and R respectively.
(ii) By taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S
(iii) Taking S as centre and with the same radius as before, draw an arc such that it is intersecting the arc at T as shown in figure
(iv) Take S and T as centres, draw arcs of same radius to intersect each other at U.
(v) Join PU. Let this intersect the arc at V. Now take Q and V as centres and with radius more than 1 / 2 QV, draw arcs to intersects each other at W.
(vi) Join PW which is the required ray making 1350 with the line l
6. Draw an angle of measure 45° and bisect it.
Solutions:
Following steps are followed to construct an angle of measure 450 and its bisector.
(i) Using the protractor ∠POQ of 450 measure may be formed on a line l
(ii) Draw an arc of convenient radius with centre as O. Let this intersects both rays of angle 450 at points A and B
(iii) Take A and B as centres, draw arcs of radius more than 1 / 2 AB in the interior of angle of 450. Let these intersect each other at C. Join OC
OC is the required bisector of 450 angle

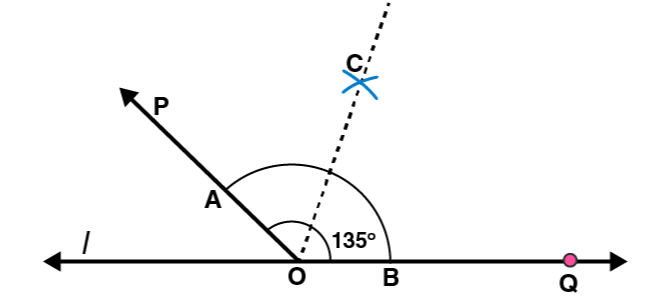
7. Draw an angle of measure 135° and bisect it.
Solutions:
Following steps are followed to construct an angle of measure 1350 and its bisector.
(i) By using a protractor ∠POQ of 1350 measure may be formed on a line l
(ii) Draw an arc of convenient radius by taking O as centre. Let this intersect both rays of angle 1350 at points A and B respectively.
(iii) Take A and B as centres, draw arcs of radius more than 1 / 2 AB in the interior of angle of 1350. Let these intersect each other at C. Join OC.
OC is the required bisector of 1350 angle
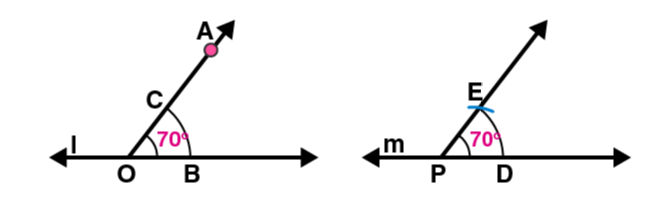
8. Draw an angle of 700. Make a copy of it using only a straight edge and compasses.
Solutions:
Following steps are followed to construct an angle of measure 700 and its copy.
(i) Draw a line l and mark a point O on it. Now place the centre of protractor at point O and the zero edge along line l.
(ii) Mark a point A at an angle of measure 700. Join OA. Now OA is the ray making 700 with line l. With point O as centre, draw an arc of convenient radius in the interior of 700 angle. Let this intersects both rays of angle 700 at points B and C respectively
(iii) Draw a line m and mark a point P on it. Again draw an arc with same radius as before and P as centre. Let it cut the line m at point D
(iv) Adjust the compasses up to the length of BC. With this radius draw an arc taking D as centre which intersects the previously drawn arc at point E.
(v) Join PE. Here PE is the required ray which makes same angle of measure 700 with the line m