Exercise 1.2 Page: 20

1. Represent these numbers on the number line.

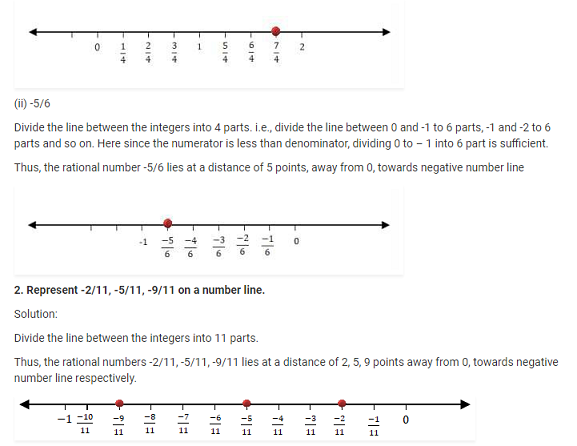
(i) 7/4

(ii) -5/6

Solution:

(i) 7/4

Divide the line between the whole numbers into 4 parts. i.e., divide the line between 0 and 1 to 4 parts, 1 and 2 to 4 parts and so on.

Thus, the rational number 7/4 lies at a distance of 7 points away from 0 towards positive number line.

3. Write five rational numbers which are smaller than 2.

Solution:

The number 2 can be written as 20/10

Hence, we can say that, the five rational numbers which are smaller than 2 are:

2/10, 5/10, 10/10, 15/10, 19/10

4. Find the rational numbers between -2/5 and ½.

Solution:

Let us make the denominators same, say 50.

-2/5 = (-2 × 10)/(5 × 10) = -20/50

½ = (1 × 25)/(2 × 25) = 25/50

Ten rational numbers between -2/5 and ½ = ten rational numbers between -20/50 and 25/50

Therefore, ten rational numbers between -20/50 and 25/50 = -18/50, -15/50, -5/50, -2/50, 4/50, 5/50, 8/50, 12/50, 15/50, 20/50

5. Find five rational numbers between.

(i) 2/3 and 4/5

(ii) -3/2 and 5/3

(iii) ¼ and ½

Solution:

(i) 2/3 and 4/5

Let us make the denominators same, say 60

i.e., 2/3 and 4/5 can be written as:

2/3 = (2 × 20)/(3 × 20) = 40/60

4/5 = (4 × 12)/(5 × 12) = 48/60

Five rational numbers between 2/3 and 4/5 = five rational numbers between 40/60 and 48/60

Therefore, Five rational numbers between 40/60 and 48/60 = 41/60, 42/60, 43/60, 44/60, 45/60

(ii) -3/2 and 5/3

Let us make the denominators same, say 6

i.e., -3/2 and 5/3 can be written as:

-3/2 = (-3 × 3)/(2× 3) = -9/6

5/3 = (5 × 2)/(3 × 2) = 10/6

Five rational numbers between -3/2 and 5/3 = five rational numbers between -9/6 and 10/6

Therefore, Five rational numbers between -9/6 and 10/6 = -1/6, 2/6, 3/6, 4/6, 5/6

(iii) ¼ and ½

Let us make the denominators same, say 24.

i.e., ¼ and ½ can be written as:

¼ = (1 × 6)/(4 × 6) = 6/24

½ = (1 × 12)/(2 × 12) = 12/24

Five rational numbers between ¼ and ½ = five rational numbers between 6/24 and 12/24

Therefore, Five rational numbers between 6/24 and 12/24 = 7/24, 8/24, 9/24, 10/24, 11/24

6. Write five rational numbers greater than -2.

Solution:

-2 can be written as – 20/10

Hence, we can say that, the five rational numbers greater than -2 are

-10/10, -5/10, -1/10, 5/10, 7/10

7. Find ten rational numbers between 3/5 and ¾,

Solution:

Let us make the denominators same, say 80.

3/5 = (3 × 16)/(5× 16) = 48/80

3/4 = (3 × 20)/(4 × 20) = 60/80

Ten rational numbers between 3/5 and ¾ = ten rational numbers between 48/80 and 60/80

Therefore, ten rational numbers between 48/80 and 60/80 = 49/80, 50/80, 51/80, 52/80, 54/80, 55/80, 56/80, 57/80, 58/80, 59/80