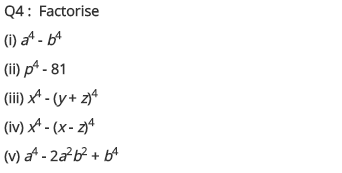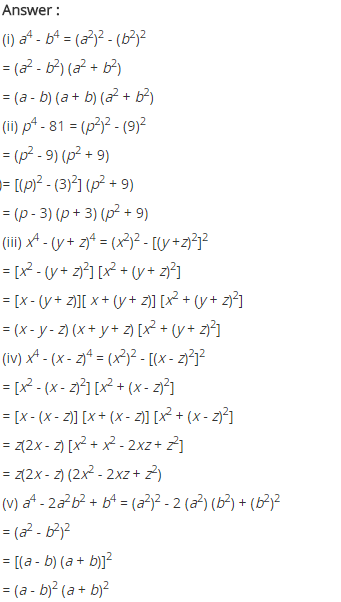Question 3.
Factorise the following polynomials.
(a) 6p(p – 3) + 1 (p – 3)
(b) 14(3y – 5z)³ + 7(3y – 5z)²
Solution:
(a) 6p(p – 3) + 1 (p – 3) = (p – 3) (6p + 1)
(b) 14(3y – 5z)³ + 7(3y – 5z)²
= 7(3y – 5z)² [2(3y – 5z) +1]
= 7(3y – 5z)² (6y – 10z + 1)

Question 4.
Factorise the following:
(a) p²q – pr² – pq + r²
(b) x² + yz + xy + xz
Solution:
(a) p²q – pr² – pq + r²
= (p²q – pq) + (-pr² + r2)
= pq(p – 1) – r²(p – 1)
= (p – 1) (pq – r²)

(b) x² + yz + xy + xz
= x² + xy +xz + yz
= x(x + y) + z(x + y)
= (x + y) (x + z)

Question 5.
Factorise the following polynomials.
(a) xy(z² + 1) + z(x² + y²)
(b) 2axy² + 10x + 3ay² + 15
Solution:
(a) xy(z² + 1) + z(x² + y²)
= xyz² + xy + 2x² + zy²
= (xyz² + zx²) + (xy + zy²)
= zx(yz + x) + y(x + yz)
= zx(x + yz) + y(x + yz)
= (x + yz) (zx + y)

(b) 2axy² + 10x + 3ay² + 15
= (2axy² + 3ay²) + (10x + 15)
= ay²(2x + 3) +5(2x + 3)
= (2x + 3) (ay² + 5)

Question 6.
Factorise the following expressions.
(а) x² + 4x + 8y + 4xy + 4y²
(b) 4p² + 2q² + p²q² + 8
Solution:
(a) x² + 4x + 8y + 4xy + 4y²
= (x² + 4xy + 4y²) + (4x + 8y)
= (x + 2y)² + 4(x + 2y)
= (x + 2y)(x + 2y + 4)

(b) 4p² + 2q² + p²q² + 8
= (4p² + 8) + (p²q² + 2q²)
= 4(p² + 2) + q²(p² + 2)
= (p² + 2)(4 + q²)

Question 7.
Factorise:
(a) a² + 14a + 48
(b) m² – 10m – 56
Solution:
(a) a² + 14a + 48
= a² + 6a + 8a + 48
[6 + 8 = 14 ; 6 × 8 = 48]
= a(a + 6) + 8(a + 6)
= (a + 6) (a + 8)

(b) m² – 10m – 56
= m² – 14m + 4m – 56
[14 – 4 = 10; 4 × 4 = 56]
= m(m – 14) + 6(m – 14)
= (m – 14) (m + 6)

Question 8.
Factorise:
(a) x⁴ – (x – y)⁴
(b) 4x² + 9 – 12x – a² – b² + 2ab
Solution:
(a) x⁴ – (x – y)⁴
= (x²)² – [(x – y)²]²
= [x² – (x – y)²] [x² + (x – y)²]
= [x + (x – y] [x – (x – y)] [x² + x² – 2xy + y²]
= (x + x – y) (x – x + y)[2x² – 2xy + y²]
= (2x – y) y(2x² – 2xy + y²)
= y(2x – y) (2x² – 2xy + y²)

(b) 4x² + 9 – 12x – a² – b² + 2ab
= (4x² – 12x + 9) – (a² + b² – 2ab)
= (2x – 3)² – (a – b)²
= [(2x – 3) + (a – b)] [(2x – 3) – (a – b)]
= (2x – 3 + a – b)(2x – 3 – a + b)

Factorisation Class 8 Extra Questions Short Answer Type

Question 9.
Factorise the following polynomials.
(a) 16x⁴ – 81
(b) (a – b)² + 4ab
Solution:
(a) 16x⁴ – 81
= (4x²)² – (9)2
= (4x² + 9)(4x² – 9)
= (4x² + 9)[(2x)² – (3)²]
= (4x² + 9)(2x + 3) (2x – 3)

(b) (a – b)² + 4ab
= a² – 2ab + b² + 4ab
= a² + 2ab + b²
= (a + b)²

Question 10.
Factorise:
(а) 14m⁵n⁴p² – 42m⁷n³p⁷ – 70m⁶n⁴p³
(b) 2a²(b² – c²) + b²(2c² – 2a²) + 2c²(a² – b²)
Solution:
(a) 14m⁵n⁴p² – 42m⁷n³p⁷ – 70m⁶n⁴p³
= 14m⁵n³p²(n – 3m²p⁵ – 5mnp)

(b) 2a²(b² – c²) + b²(2c² – 2a²) + 2c²(a² – b²)
= 2a²(b² – c²) + 2b²(c² – a²) + 2c²(a² – b²)
= 2[a²(b² – c²) + b²(c² – a²) + c²(a² – b²)]

= 2 × 0
= 0

Question 11.
Factorise:
(a) (x + y)² – 4xy – 9z²
(b) 25x² – 4y² + 28yz – 49z²
Solution:
(a) (x + y)² – 4xy – 9z²
= x² + 2xy + y² – 4xy – 9z²
= (x² – 2xy + y²) – 9z²
= (x – y)² – (3z)²
= (x – y + 3z) (x – y – 3z)

(b) 25x² – 4y² + 28yz – 49z²
= 25x² – (4y² – 28yz + 49z²)
= (5x)² – (2y – 7)²
= (5x + 2y – 7) [5x – (2y – 7)]
= (5x + 2y – 7) (5x – 2y + 7)