Exercise 3.1 Page: 41
1. Given here are some figures.
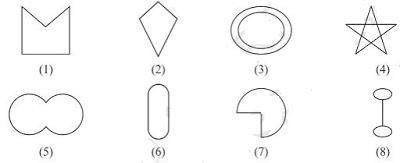
Classify each of them on the basis of the following.
Simple curve (b) Simple closed curve (c) Polygon
(d) Convex polygon (e) Concave polygon
Solution:
a) Simple curve: 1, 2, 5, 6 and 7
b) Simple closed curve: 1, 2, 5, 6 and 7
c) Polygon: 1 and 2
d) Convex polygon: 2
e) Concave polygon: 1
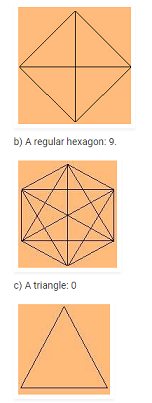
2. How many diagonals does each of the following have?
a) A convex quadrilateral (b) A regular hexagon (c) A triangle
Solution:
a) A convex quadrilateral: 2.
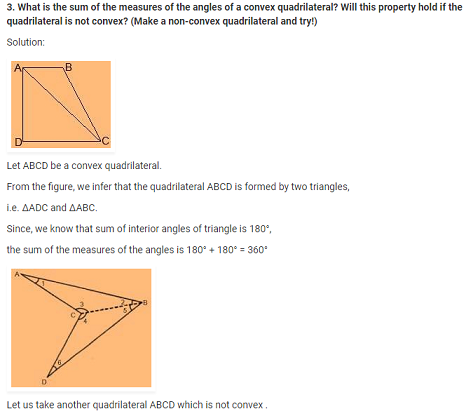
Join BC, Such that it divides ABCD into two triangles ΔABC and ΔBCD. In ΔABC,
∠1 + ∠2 + ∠3 = 180° (angle sum property of triangle)
In ΔBCD,
∠4 + ∠5 + ∠6 = 180° (angle sum property of triangle)
∴, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 180° + 180°
⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
Thus, this property hold if the quadrilateral is not convex.
4. Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
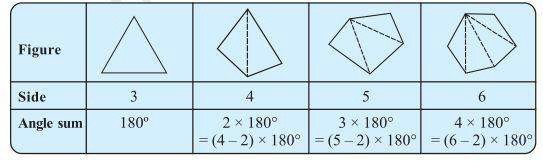
What can you say about the angle sum of a convex polygon with number of sides? (a) 7 (b) 8 (c) 10 (d) n
Solution:
The angle sum of a polygon having side n = (n-2)×180°
a) 7
Here, n = 7
Thus, angle sum = (7-2)×180° = 5×180° = 900°
b) 8
Here, n = 8
Thus, angle sum = (8-2)×180° = 6×180° = 1080°
c) 10
Here, n = 10
Thus, angle sum = (10-2)×180° = 8×180° = 1440°
d) n
Here, n = n
Thus, angle sum = (n-2)×180°
5. What is a regular polygon?
State the name of a regular polygon of
(i) 3 sides (ii) 4 sides (iii) 6 sides Solution:
Regular polygon: A polygon having sides of equal length and angles of equal measures is called regular polygon. i.e., A regular polygon is both equilateral and equiangular.
(i) A regular polygon of 3 sides is called equilateral triangle.
(ii) A regular polygon of 4 sides is called square.
(iii) A regular polygon of 6 sides is called regular hexagon.
6. Find the angle measure x in the following figures.

Solution:
a) The figure is having 4 sides. Hence, it is a quadrilateral. Sum of angles of the quadrilateral = 360°
⇒ 50° + 130° + 120° + x = 360°
⇒ 300° + x = 360°
⇒ x = 360° – 300° = 60°
b) The figure is having 4 sides. Hence, it is a quadrilateral. Also, one side is perpendicular forming right angle.
Sum of angles of the quadrilateral = 360°
⇒ 90° + 70° + 60° + x = 360°
⇒ 220° + x = 360°
⇒ x = 360° – 220° = 140°
c) The figure is having 5 sides. Hence, it is a pentagon.

Sum of angles of the pentagon = 540° Two angles at the bottom are linear pair.
∴, 180° – 70° = 110°
180° – 60° = 120°
⇒ 30° + 110° + 120° + x + x = 540°
⇒ 260° + 2x = 540°
⇒ 2x = 540° – 260° = 280°
⇒ 2x = 280°
= 140°
d) The figure is having 5 equal sides. Hence, it is a regular pentagon. Thus, its all angles are equal.
5x = 540°
⇒ x = 540°/5
⇒ x = 108°
7.
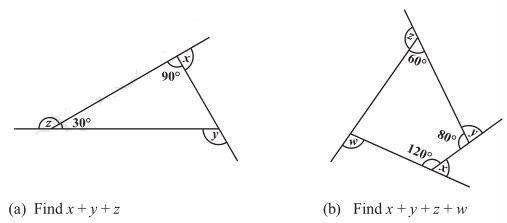
Solution:
a) Sum of all angles of triangle = 180°
One side of triangle = 180°- (90° + 30°) = 60°
x + 90° = 180° ⇒ x = 180° – 90° = 90°
y + 60° = 180° ⇒ y = 180° – 60° = 120°
z + 30° = 180° ⇒ z = 180° – 30° = 150°
x + y + z = 90° + 120° + 150° = 360°
b) Sum of all angles of quadrilateral = 360°
One side of quadrilateral = 360°- (60° + 80° + 120°) = 360° – 260° = 100°
x + 120° = 180° ⇒ x = 180° – 120° = 60°
y + 80° = 180° ⇒ y = 180° – 80° = 100°
z + 60° = 180° ⇒ z = 180° – 60° = 120°
w + 100° = 180° ⇒ w = 180° – 100° = 80°
x + y + z + w = 60° + 100° + 120° + 80° = 360°