Selling Price: The price at which an item is sold is called its selling price. It is written in short as SP.

Profit: If SP > CP, then we make a profit.
Profit = SP – CP

Loss: If CP > SP, then we make a loss.
Loss = CP – SP
Note: If SP = CP, then we are in a no profit no loss situation.

Profit/Loss Percent:
Profit/Loss is always calculated on the CP.

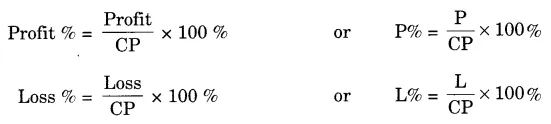
Overall Gain:
Overall gain = Combined SP – Combined CP

Overall Loss:
Overall loss = Combined CP – Combined SP.
Note: We need to find the combined CP and SP to say whether there was an overall profit or loss.

Sales Tax/Value Added Tax
Sales tax is charged at a specified rate on the sale price of an item by the state government and is added to the bill amount. It is different for different items and also for different states.
Amount of Sales Tax = Tax% of the bill amount
These days, the prices include the tax known as Value Added Tax (VAT).

Compound Interest
Interest: Interest is the extra money paid by institutions like banks or post offices on money which is deposited (kept) with them. Interest is also paid by people when they borrow money. The money deposited or borrowed is called the principal. Interest is generally given in per cent for a period of one year.

Simple interest (SI): The interest is called simple when the principal does not change.

The formula for Simple Interest: Simple interest on a principal of ₹ P at R% rate of interest per year for T years is given by

Rate Compounded Annually or Half Yearly (Semi-Annually)
The word annually mentioned after the rate means that the interest is charged at the end of every year, whereas the rate is given for one year.

We could also have interest rates compounded half-yearly or quarterly. This means that the rate for the one-half year (i.e., 6 months) is half of the rate given for one year and the time period is of two half years because interest is charged twice a year.
So if a sum of ₹ 50,000 is taken for 1 year at 10% p.a. compounded semi-annually, it means time period = 2 half years (i.e., 1 × 2) and rate = 12 × 10% = 5%.

Note:

1. The time period for which the interest is calculated and added each time to form a new principle is called the conversion period or time period.
2. If interest is compounded half-yearly, then there are two conversion periods in a year each after 6 months. In such situations, we compute the interest two times. So, the time period becomes twice and the rate becomes half of the annual rate.
3. If interest is compounded quarterly, then there are four conversion periods in a year each after 3 months. In such situations, we compute the interest four times. So, the time period becomes four times and the rate becomes one-fourth of the annual rate.

Applications of Compound Interest Formula
We use the compound interest formula to find

• Increase (or decrease) in population.
• The growth of bacteria if the rate of growth is known.
• The value of an item, if its price increases or decreases in the intermediate years.

Note: For increase, R is positive and for decrease, R is negative.