What are Quadrilaterals?

Quadrilaterals are one type of polygon which has four sides and four vertices and four angles along with 2 diagonals. There are various types of quadrilaterals.

Types of Quadrilaterals

The classification of quadrilaterals are dependent on the nature of sides or angles of a quadrilateral and they are as follows:

• Trapezium
• Kite
• Parallelogram
• Square
• Rectangle
• Rhombus

Polygons

A simple closed curve made up of only line segments is called a polygon.
Various examples of polygons are Squares, Rectangles, Pentagons etc.
Note:
The sides of a polygon do not cross each other.
For example, the figure given below is not a polygon because its sides cross each other.

Classification of Polygons on the Basis of Number of Sides / Vertices

Polygons are classified according to the number of sides they have. The following lists the different types of polygons based on the number of sides they have:

• When there are three sides, it is triangle
• When there are four sides, it is quadrilateral
• When there are fives sides, it is pentagon
• When there are six sides, it is hexagon
• When there are seven sides, it is heptagon
• When there are  eight sides, it is octagon
• When there are nine sides, it is nonagon
• When there are ten sides, it is decagon

Diagonals

A diagonal is a line segment connecting two non-consecutive vertices of a polygon.

As we can see for the above quadrilateral, if we join one of the diagonals of the quadrilateral, we get two triangles.
The sum of all the interior angles of the two triangles is equal to the sum of all the interior angles of the quadrilateral, which is equal to 360${}^{}$ = $(4-2)\times {180}^{\circ }$.
So, if there is a polygon which has n sides, we can make (n – 2) non-overlapping triangles which will perfectly cover that polygon.

Elements of a Parallelogram

• There are four sides and four angles in a parallelogram.
• The opposite sides and opposite angles of a parallelogram are equal.
• In the parallelogram ABCD, the sides $\overline{AB}$ and $\overline{CD}$ are opposite sides and the sides $\overline{AB}$ and $\overline{BC}$ are adjacent sides.
• Similarly, $\angle ABC$ and $\angle ADC$ are opposite angles and  $\angle ABC$ and $\angle BCD$ are adjacent angles.

Angles of a Parallelogram

The opposite angles of a parallelogram are equal.
In the parallelogram ABCD, $\angle ABC=\angle ADC$ and $\angle DAB=\angle BCD$.

The adjacent angles in a parallelogram are supplementary.
$\therefore$ In the parallelogram ABCD, $\angle ABC+\angle BCD=\angle ADC+\angle DAB={180}^{\circ }$

Properties of Special Parallelograms

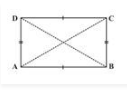
Rectangle

A rectangle is a parallelogram with equal angles and each angle is equal to 90${}^{}$.
Properties:

• Opposite sides of a rectangle are parallel and equal.
• The length of diagonals of a rectangle is equal.
• All the interior angles of a rectangle are equal to 90${}^{}$.
• The diagonals of a rectangle bisect each other at the point of intersection.

Square

A square is a rectangle with equal sides. All the properties of a rectangle are also true for a square.
In a square the diagonals:

• bisect one another
• are of equal length
• are perpendicular to one another