Introduction: Rational Numbers
- A rational number is defined as a number that can be expressed in the form p/q where p and q are integers and q≠0.
Equivalent Rational Numbers
- By multiplying or dividing the numerator and denominator of a rational number by a same non zero integer, we obtain another rational number equivalent to the given rational number.These are called equivalent fractions.
Rational Numbers in Standard Form
- A rational number is said to be in the standard form if its denominator is a positive integer and the numerator and denominator have no common factor other than 1.
Example : 2/3, 4/5 , 7/9 etc.
LCM
- The least common multiple (LCM) of two numbers is the smallest number (≠0) that is a multiple of both.
- Example: LCM of 3 and 4 can be calculated as shown below:
Multiples of 3: 0, 3, 6, 9, 12,15
Multiples of 4: 0, 4, 8, 12, 16
LCM of 3 and 4 is 12.
Rational Numbers between Two Rational Numbers
- There are unlimited number(infinite number) of rational numbers between any two rational numbers.
- Example: List some of the rational numbers between −35 and −13.
Solution: L.C.M. of 5 and 3 is 15.
⇒ The given equations can be written as -9/15 and -5/15 .
⇒ −615,−715,−815 are the rational numbers between −35 and −13.
Note: These are only few of the rational numbers between −35 and −13. There are infinte number of rational numbers between them. Following the same procedure, many more rational numbers can be inserted between them.
Properties of Rational Numbers

Addition of Rational Numbers
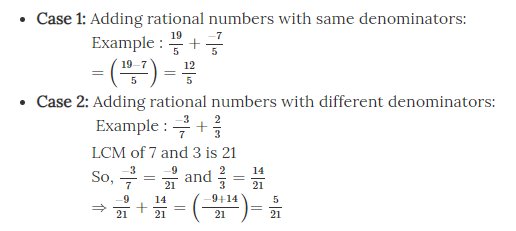
Subtraction of Rational Numbers

Multiplication and Division of Rational Numbers
Multiplication of Rational Numbers

Negatives and Reciprocals

Additive Inverse of a Rational Number

Rational Numbers on a Number Line

Comparison of Rational Numbers
