What are Solids in Maths?

Dimensions

• Dimension is a measurable length along a direction.
• Dimensions are length, breadth (or width) or height (or depth).
• A point is dimensionless.
• Based on the number of dimensions a figure has, there are one-dimensional, two-dimensional and three-dimensional figures.

You Already Know These Shapes!!

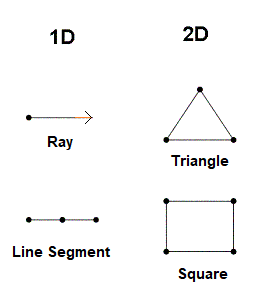
1D and 2D figures

• One-dimensional figures do not enclose any area and have only one direction.
  Example: A ray or a line segment.
• Two-dimensional figures have an area associated with them.
  They have length and breadth or width.
  They are usually plane figures, like squares, rectangles and circles.

Solid Shapes

• Solid shapes have length, breadth or width and depth or height.
• They are called 3D or three-dimensional shapes.
• Example: Cuboids, Cylinders, Spheres and Pyramids.

Visualising solid shapes

• Solid shapes can be visualised in different ways.
• Solid shapes can be formed by placing some solid shapes side by side to form a new solid shape.
• Example: (i) A cylinder is formed by stacking up circles vertically.
  (ii) Cubes can be formed by placing cubes side by side.

Visualising solid objects by viewing the smallest unit

• A solid can be visualised by breaking it down to the smallest unit.
• For example, a cube of dimensions (3cm x 3cm x 3cm) can be made up of 27 small cubes of dimensions (1cm x 1cm x 1cm).

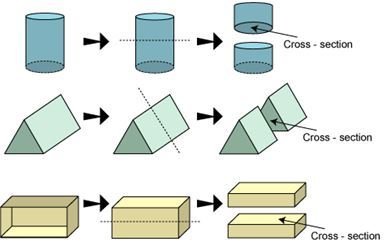
Viewing sections of a solid by slicing or cutting

• If you cut or slice a solid we get to view the cross-section.
  Example: If a loaf of bread is cut vertically, then the crosssection is almost a square. But if it is cut or sliced horizontally, the cross-section is a rectangle.
• Similarly, other solid shapes can be sliced in order to find their 2D cross-sectional shapes.
  Example: A cucumber cut vertically gives a circle.

Viewing sections of a solid by using shadows

• Shadows can be used to view 3D objects as 2D shapes.
• Example: The shadows of a cylinder are shown below.

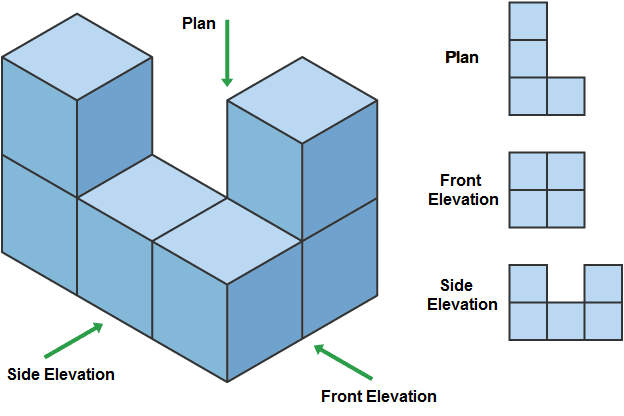
Different views of a Solid

• A solid can be visualised by looking at it from different angles, namely: (i) Front view (ii) Top view (iii) Side view.
• Example: The different views of a figure are shown below.

Quantities Associated with a Solid

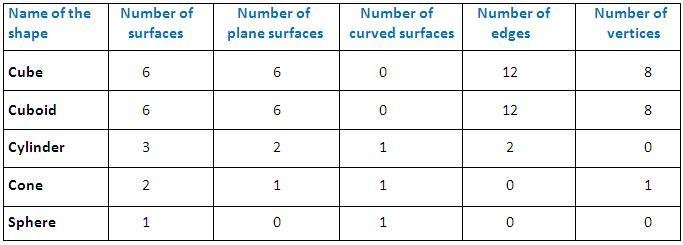
Faces, edges and vertices

• The corners of a solid shape are called its vertices.
• The line segment joining two vertices is called an edge, or when two planes of a solid meet it forms an edge.
• The surfaces of a solid shape are called as its face.

The table below shows the number of faces, edges and vertices some solid shapes have.

Nets of Solid Shapes

Building 3-D objects

A net is a flattened out skeletal outline or a blueprint of a solid which can be folded along the edges to create solid.The same solid can have multiple nets.

Example: A net for a cube box.

Representing 3D Shapes on a Paper

Drawing solids on a flat surface

• Solid shapes can be represented on a 2D flat surface like paper.
• This is done by drawing oblique sketches, to make it appear 3D. This is called as 2D representation of a 3D solid.

Obliques sketches

• Oblique sketches do not have the exact length of a solid shape but appears exactly like the solid shape.
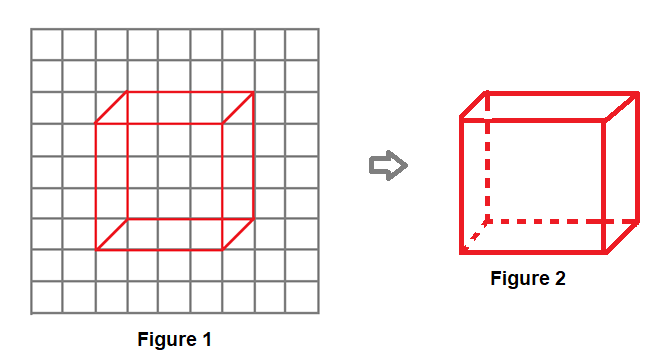
• Example: Drawing an oblique sketch of a cube:
  Step 1: Draw the front and the opposite faces.
  Step 2: Join the corresponding corners. (Figure 1)
  Step 3: Redraw using dotted lines for hidden edges. (Figure 2)

This gives the oblique sketch of the cube.

Isometric sketches

• Isometric sketches have measurements equal to that of the solid.
• They are usually drawn on an isometric dotted paper.
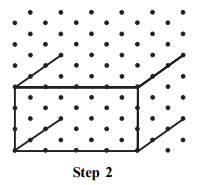
• Example: Drawing an isometric sketch of a cuboid of dimensions 4 $\times$ 3 $\times$ 3:

           Step 1: Draw a rectangle to show the front face of the cuboid.

           Step 2: Draw four parallel line segments of length three starting from the four corners of the rectangle.

           Step 3: Connect the corresponding corners using appropriate line segments.

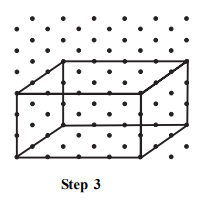
            Step 4: The figure thus obtained is the isometric sketch of the cuboid.