Exercise 12.4 Page: 246
1. Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.
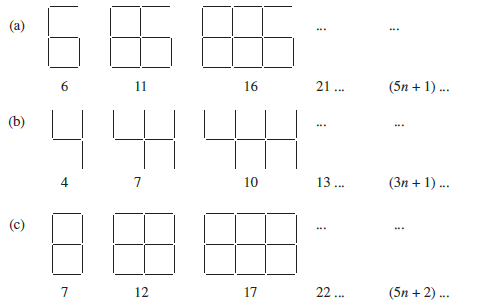


Then,
The number of segments required to form 5 digits = ((5 × 5) + 2)
= (25 + 2)
= 27
The number of segments required to form 10 digits = ((5 × 10) + 2)
= (50 + 2)
= 52
The number of segments required to form 100 digits = ((5 × 100) + 1)
= (500 + 2)
= 502
2. Use the given algebraic expression to complete the table of number patterns.
| S. No. | Expression | Terms | |||||||||
| 1st | 2nd | 3rd | 4th | 5th | … | 10th | … | 100th | … | ||
| (i) | 2n – 1 | 1 | 3 | 5 | 7 | 9 | – | 19 | – | – | – |
| (ii) | 3n + 2 | 5 | 8 | 11 | 14 | – | – | – | – | – | – |
| (iii) | 4n + 1 | 5 | 9 | 13 | 17 | – | – | – | – | – | – |
| (iv) | 7n + 20 | 27 | 34 | 41 | 48 | – | – | – | – | – | – |
| (v) | n2 + 1 | 2 | 5 | 10 | 17 | – | – | – | – | 10001 | – |
Solution:-
(i) From the table (2n – 1)
Then, 100th term =?
Where n = 100
= (2 × 100) – 1
= 200 – 1
= 199
(ii) From the table (3n + 2)
5th term =?
Where n = 5
= (3 × 5) + 2
= 15 + 2
= 17
Then, 10th term =?
Where n = 10
= (3 × 10) + 2
= 30 + 2
= 32
Then, 100th term =?
Where n = 100
= (3 × 100) + 2
= 300 + 2
= 302
(iii) From the table (4n + 1)
5th term =?
Where n = 5
= (4 × 5) + 1
= 20 + 1
= 21
Then, 10th term =?
Where n = 10
= (4 × 10) + 1
= 40 + 1
= 41
Then, 100th term =?
Where n = 100
= (4 × 100) + 1
= 400 + 1
= 401
(iv) From the table (7n + 20)
5th term =?
Where n = 5
= (7 × 5) + 20
= 35 + 20
= 55
Then, 10th term =?
Where n = 10
= (7 × 10) + 20
= 70 + 20
= 90
Then, 100th term =?
Where n = 100
= (7 × 100) + 20
= 700 + 20
= 720
(v) From the table (n2 + 1)
5th term =?
Where n = 5
= (52) + 1
= 25+ 1
= 26
Then, 10th term =?
Where n = 10
= (102) + 1
= 100 + 1
= 101
So the table is completed below.
| S. No. | Expression | Terms | |||||||||
| 1st | 2nd | 3rd | 4th | 5th | … | 10th | … | 100th | … | ||
| (i) | 2n – 1 | 1 | 3 | 5 | 7 | 9 | – | 19 | – | 199 | – |
| (ii) | 3n + 2 | 5 | 8 | 11 | 14 | 17 | – | 32 | – | 302 | – |
| (iii) | 4n + 1 | 5 | 9 | 13 | 17 | 21 | – | 41 | – | 401 | – |
| (iv) | 7n + 20 | 27 | 34 | 41 | 48 | 55 | – | 90 | – | 720 | – |
| (v) | n2 + 1 | 2 | 5 | 10 | 17 | 26 | – | 101 | – | 10001 | – |