Exercise 5.2 Page: 110

1. State the property that is used in each of the following statements?

(i) If a ∥ b, then ∠1 = ∠5.

Solution:-

Corresponding angles property is used in the above statement.

(ii) If ∠4 = ∠6, then a ∥ b.

Solution:-

Alternate interior angles property is used in the above statement.

(iii) If ∠4 + ∠5 = 180^o, then a ∥ b.

Solution:-

Interior angles on the same side of transversal are supplementary.

2. In the adjoining figure, identify

(i) The pairs of corresponding angles.

Solution:-

By observing the figure, the pairs of corresponding angle are,

∠1 and ∠5, ∠4 and ∠8, ∠2 and ∠6, ∠3 and ∠7

(ii) The pairs of alternate interior angles.

Solution:-

By observing the figure, the pairs of alternate interior angle are,

∠2 and ∠8, ∠3 and ∠5

(iii) The pairs of interior angles on the same side of the transversal.

Solution:-

By observing the figure, the pairs of interior angles on the same side of the transversal are ∠2 and ∠5, ∠3 and ∠8

(iv) The vertically opposite angles.

Solution:-

By observing the figure, the vertically opposite angles are,

∠1 and ∠3, ∠5 and ∠7, ∠2 and ∠4, ∠6 and ∠8

3. In the adjoining figure, p ∥ q. Find the unknown angles.

Solution:-

By observing the figure,

∠d = ∠125^o … [∵ corresponding angles]

We know that, Linear pair is the sum of adjacent angles is 180^o

Then,

= ∠e + 125^o = 180^o … [Linear pair]

= ∠e = 180^o – 125^o

= ∠e = 55^o

From the rule of vertically opposite angles,

∠f = ∠e = 55^o

∠b = ∠d = 125^o

By the property of corresponding angles,

∠c = ∠f = 55^o

∠a = ∠e = 55^o

4. Find the value of x in each of the following figures if l ∥ m.

(i)

Solution:-

Let us assume other angle on the line m be ∠y,

Then,

By the property of corresponding angles,

∠y = 110^o

We know that Linear pair is the sum of adjacent angles is 180^o

Then,

= ∠x + ∠y = 180^o

= ∠x + 110^o = 180^o

= ∠x = 180^o – 110^o

= ∠x = 70^o

(ii)

Solution:-

By the property of corresponding angles,

∠x = 100^o

5. In the given figure, the arms of two angles are parallel.

If ∠ABC = 70^o, then find

(i) ∠DGC

(ii) ∠DEF

Solution:-

(i) Let us consider that AB ∥ DG

BC is the transversal line intersecting AB and DG

By the property of corresponding angles,

∠DGC = ∠ABC

Then,

∠DGC = 70^o

(ii) Let us consider that BC ∥ EF

DE is the transversal line intersecting BC and EF

By the property of corresponding angles,

∠DEF = ∠DGC

Then,

∠DEF = 70^o

6. In the given figures below, decide whether l is parallel to m.

(i)

Solution:-

Let us consider the two lines l and m,

n is the transversal line intersecting l and m.

We know that the sum of interior angles on the same side of transversal is 180^o.

Then,

= 126^o + 44^o

= 170^o

But, the sum of interior angles on the same side of transversal is not equal to 180^o.

So, line l is not parallel to line m.

(ii)

Solution:-

Let us assume ∠x be the vertically opposite angle formed due to the intersection of the straight line l and transversal n,

Then, ∠x = 75^o

Let us consider the two lines l and m,

n is the transversal line intersecting l and m.

We know that the sum of interior angles on the same side of transversal is 180^o.

Then,

= 75^o + 75^o

= 150^o

But, the sum of interior angles on the same side of transversal is not equal to 180^o.

So, line l is not parallel to line m.

(iii)

Solution:-

Let us assume ∠x be the vertically opposite angle formed due to the intersection of the Straight line l and transversal line n,

Let us consider the two lines l and m,

n is the transversal line intersecting l and m.

We know that the sum of interior angles on the same side of transversal is 180^o.

Then,

= 123^o + ∠x

= 123^o + 57^o

= 180^o

∴The sum of interior angles on the same side of transversal is equal to 180^o.

So, line l is parallel to line m.

(iv)

Solution:-

Let us assume ∠x be the angle formed due to the intersection of the Straight line l and transversal line n,

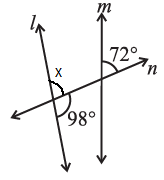
We know that Linear pair is the sum of adjacent angles is equal to 180^o.

= ∠x + 98^o = 180^o

= ∠x = 180^o – 98^o

= ∠x = 82^o

Now, we consider ∠x and 72^o are the corresponding angles.

For l and m to be parallel to each other, corresponding angles should be equal.

But, in the given figure corresponding angles measures 82^o and 72^o respectively.

∴Line l is not parallel to line m.