Exercise 9.1 Page: 182
1. List five rational numbers between:
(i) -1 and 0
Solution:-
The five rational numbers between -1 and 0 are,
-1< (-2/3) < (-3/4) < (-4/5) < (-5/6) < (-6/7) < 0
(ii) -2 and -1
Solution:-
The five rational numbers between -2 and -1 are,
-2 < (-8/7) < (-9/8) < (-10/9) < (-11/10) < (-12/11) < -1
(iii) -4/5 and -2/3
Solution:-
The five rational numbers between -4/5 and -2/3 are,
-4/5 < (-13/12) < (-14/13) < (-15/14) < (-16/15) < (-17/16) < -2/3
(iv) -1/2 and 2/3
Solution:-
The five rational numbers between -1/2 and 2/3 are,
-1/2 < (-1/6) < (0) < (1/3) < (1/2) < (20/36) < 2/3
2. Write four more rational numbers in each of the following patterns:
(i) -3/5, -6/10, -9/15, -12/20, …..
Solution:-
In the above question, we can observe that the numerator and denominator are the multiples of 3 and 5.
= (-3 × 1)/ (5 × 1), (-3 × 2)/ (5 × 2), (-3 × 3)/ (5 × 3), (-3 × 4)/ (5 × 4)
Then, next four rational numbers in this pattern are,
= (-3 × 5)/ (5 × 5), (-3 × 6)/ (5 × 6), (-3 × 7)/ (5 × 7), (-3 × 8)/ (5 × 8)
= -15/25, -18/30, -21/35, -24/40 ….
(ii) -1/4, -2/8, -3/12, …..
Solution:-
In the above question, we can observe that the numerator and denominator are the multiples of 1 and 4.
= (-1 × 1)/ (4 × 1), (-1 × 2)/ (4 × 2), (-1 × 3)/ (1 × 3)
Then, next four rational numbers in this pattern are,
= (-1 × 4)/ (4 × 4), (-1 × 5)/ (4 × 5), (-1 × 6)/ (4 × 6), (-1 × 7)/ (4 × 7)
= -4/16, -5/20, -6/24, -7/28 ….
(iii) -1/6, 2/-12, 3/-18, 4/-24 …..
Solution:-
In the above question, we can observe that the numerator and denominator are the multiples of 1 and 6.
= (-1 × 1)/ (6 × 1), (1 × 2)/ (-6 × 2), (1 × 3)/ (-6 × 3), (1 × 4)/ (-6 × 4)
Then, next four rational numbers in this pattern are,
= (1 × 5)/ (-6 × 5), (1 × 6)/ (-6 × 6), (1 × 7)/ (-6 × 7), (1 × 8)/ (-6 × 8)
= 5/-30, 6/-36, 7/-42, 8/-48 ….
(iv) -2/3, 2/-3, 4/-6, 6/-9 …..
Solution:-
In the above question, we can observe that the numerator and denominator are the multiples of 2 and 3.
= (-2 × 1)/ (3 × 1), (2 × 1)/ (-3 × 1), (2 × 2)/ (-3 × 2), (2 × 3)/ (-3 × 3)
Then, next four rational numbers in this pattern are,
= (2 × 4)/ (-3 × 4), (2 × 5)/ (-3 × 5), (2 × 6)/ (-3 × 6), (2 × 7)/ (-3 × 7)
= 8/-12, 10/-15, 12/-18, 14/-21 ….
3. Give four rational numbers equivalent to:
(i) -2/7
Solution:-
The four rational numbers equivalent to -2/7 are,
= (-2 × 2)/ (7 × 2), (-2 × 3)/ (7 × 3), (-2 × 4)/ (7 × 4), (-2 × 5)/ (7× 5)
= -4/14, -6/21, -8/28, -10/35
(ii) 5/-3
Solution:-
The four rational numbers equivalent to 5/-3 are,
= (5 × 2)/ (-3 × 2), (5 × 3)/ (-3 × 3), (5 × 4)/ (-3 × 4), (5 × 5)/ (-3× 5)
= 10/-6, 15/-9, 20/-12, 25/-15
(iii) 4/9
Solution:-
The four rational numbers equivalent to 5/-3 are,
= (4 × 2)/ (9 × 2), (4 × 3)/ (9 × 3), (4 × 4)/ (9 × 4), (4 × 5)/ (9× 5)
= 8/18, 12/27, 16/36, 20/45
4. Draw the number line and represent the following rational numbers on it:
(i) ¾
Solution:-
We know that 3/4 is greater than 0 and less than 1.
∴it lies between 0 and 1. It can be represented on number line as,

(ii) -5/8
Solution:-
We know that -5/8 is less than 0 and greater than -1.
∴it lies between 0 and -1. It can be represented on number line as,
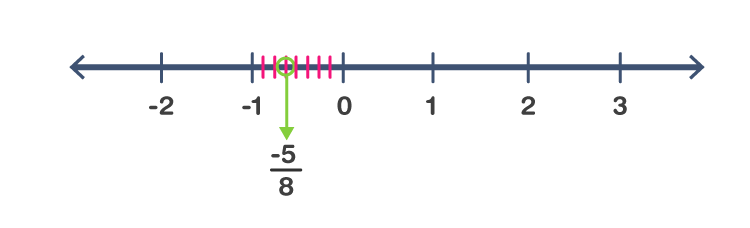

(iv) 7/8
Solution:-
We know that 7/8 is greater than 0 and less than 1.
∴it lies between 0 and 1. It can be represented on number line as,
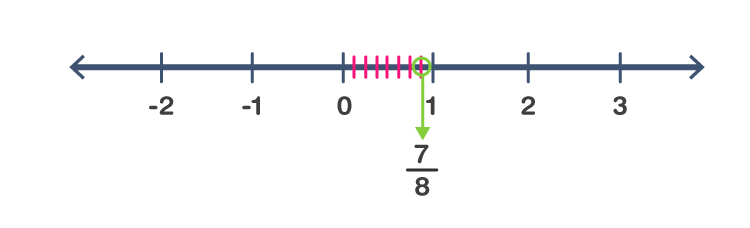
5. The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.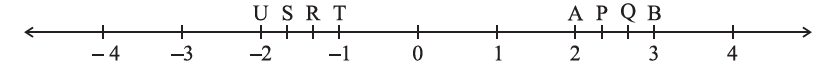
Solution:-
By observing the figure, we can say that,
The distance between A and B = 1 unit
And it is divided into 3 equal parts = AP = PQ = QB = 1/3
P = 2 + (1/3)
= (6 + 1)/ 3
= 7/3
Q = 2 + (2/3)
= (6 + 2)/ 3
= 8/3
Similarly,
The distance between U and T = 1 unit
And it is divided into 3 equal parts = TR = RS = SU = 1/3
R = – 1 – (1/3)
= (- 3 – 1)/ 3
= – 4/3
S = – 1 – (2/3)
= – 3 – 2)/ 3
= – 5/3
6. Which of the following pairs represent the same rational number?
(i) (-7/21) and (3/9)
Solution:-
We have to check if the given pair represents the same rational number.
Then,
-7/21 = 3/9
-1/3 = 1/3
∵ -1/3 ≠ 1/3
∴ -7/21 ≠ 3/9
So, the given pair does not represent the same rational number.
(ii) (-16/20) and (20/-25)
Solution:-
We have to check if the given pair represents the same rational number.
Then,
-16/20 = 20/-25
-4/5 = 4/-5
∵ -4/5 = -4/5
∴ -16/20 = 20/-25
So, the given pair represents the same rational number.
(iii) (-2/-3) and (2/3)
Solution:-
We have to check if the given pair represents the same rational number.
Then,
-2/-3 = 2/3
2/3= 2/3
∵ 2/3 = 2/3
∴ -2/-3 = 2/3
So, the given pair represents the same rational number.
(iv) (-3/5) and (-12/20)
Solution:-
We have to check if the given pair represents the same rational number.
Then,
-3/5 = – 12/20
-3/5 = -3/5
∵ -3/5 = -3/5
∴ -3/5= -12/20
So, the given pair represents the same rational number.
(v) (8/-5) and (-24/15)
Solution:-
We have to check if the given pair represents the same rational number.
Then,
8/-5 = -24/15
8/-5 = -8/5
∵ -8/5 = -8/5
∴ 8/-5 = -24/15
So, the given pair represents the same rational number.
(vi) (1/3) and (-1/9)
Solution:-
We have to check if the given pair represents the same rational number.
Then,
1/3 = -1/9
∵ 1/3 ≠ -1/9
∴ 1/3 ≠ -1/9
So, the given pair does not represent the same rational number.
(vii) (-5/-9) and (5/-9)
Solution:-
We have to check if the given pair represents the same rational number.
Then,
-5/-9 = 5/-9
∵ 5/9 ≠ -5/9
∴ -5/-9 ≠ 5/-9
So, the given pair does not represent the same rational number.
7. Rewrite the following rational numbers in the simplest form:
(i) -8/6
Solution:-
The given rational numbers can be simplified further,
Then,
= -4/3 … [∵ Divide both numerator and denominator by 2]
(ii) 25/45
Solution:-
The given rational numbers can be simplified further,
Then,
= 5/9 … [∵ Divide both numerator and denominator by 5]
(iii) -44/72
Solution:-
The given rational numbers can be simplified further,
Then,
= -11/18 … [∵ Divide both numerator and denominator by 4]
(iv) -8/10
Solution:-
The given rational numbers can be simplified further,
Then,
= -4/5 … [∵ Divide both numerator and denominator by 2]
8. Fill in the boxes with the correct symbol out of >, <, and =.
(i) -5/7 [ ] 2/3
Solution:-
The LCM of the denominators 7 and 3 is 21
∴ (-5/7) = [(-5 × 3)/ (7 × 3)] = (-15/21)
And (2/3) = [(2 × 7)/ (3 × 7)] = (14/21)
Now,
-15 < 14
So, (-15/21) < (14/21)
Hence, -5/7 [<] 2/3
(ii) -4/5 [ ] -5/7
Solution:-
The LCM of the denominators 5 and 7 is 35
∴ (-4/5) = [(-4 × 7)/ (5 × 7)] = (-28/35)
And (-5/7) = [(-5 × 5)/ (7 × 5)] = (-25/35)
Now,
-28 < -25
So, (-28/35) < (- 25/35)
Hence, -4/5 [<] -5/7
(iii) -7/8 [ ] 14/-16
Solution:-
14/-16 can be simplified further,
Then,
7/-8 … [∵ Divide both numerator and denominator by 2]
So, (-7/8) = (-7/8)
Hence, -7/8 [=] 14/-16
(iv) -8/5 [ ] -7/4
Solution:-
The LCM of the denominators 5 and 4 is 20
∴ (-8/5) = [(-8 × 4)/ (5 × 4)] = (-32/20)
And (-7/4) = [(-7 × 5)/ (4 × 5)] = (-35/20)
Now,
-32 > – 35
So, (-32/20) > (- 35/20)
Hence, -8/5 [>] -7/4
(v) 1/-3 [ ] -1/4
Solution:-
The LCM of the denominators 3 and 4 is 12
∴ (-1/3) = [(-1 × 4)/ (3 × 4)] = (-4/12)
And (-1/4) = [(-1 × 3)/ (4 × 3)] = (-3/12)
Now,
-4 < – 3
So, (-4/12) < (- 3/12)
Hence, 1/-3 [<] -1/4
(vi) 5/-11 [ ] -5/11
Solution:-
Since, (-5/11) = (-5/11)
Hence, 5/-11 [=] -5/11
(vii) 0 [ ] -7/6
Solution:-
Since every negative rational number is less than 0.
We have:
= 0 [>] -7/6
9. Which is greater in each of the following:
(i) 2/3, 5/2
Solution:-
The LCM of the denominators 3 and 2 is 6
(2/3) = [(2 × 2)/ (3 × 2)] = (4/6)
And (5/2) = [(5 × 3)/ (2 × 3)] = (15/6)
Now,
4 < 15
So, (4/6) < (15/6)
∴ 2/3 < 5/2
Hence, 5/2 is greater.
(ii) -5/6, -4/3
Solution:-
The LCM of the denominators 6 and 3 is 6
∴ (-5/6) = [(-5 × 1)/ (6 × 1)] = (-5/6)
And (-4/3) = [(-4 × 2)/ (3 × 2)] = (-12/6)
Now,
-5 > -12
So, (-5/6) > (- 12/6)
∴ -5/6 > -12/6
Hence, – 5/6 is greater.
(iii) -3/4, 2/-3
Solution:-
The LCM of the denominators 4 and 3 is 12
∴ (-3/4) = [(-3 × 3)/ (4 × 3)] = (-9/12)
And (-2/3) = [(-2 × 4)/ (3 × 4)] = (-8/12)
Now,
-9 < -8
So, (-9/12) < (- 8/12)
∴ -3/4 < 2/-3
Hence, 2/-3 is greater.
(iv) -¼, ¼
Solution:-
The given fraction is like friction,
So, -¼ < ¼
Hence ¼ is greater,

10. Write the following rational numbers in ascending order:
(i) -3/5, -2/5, -1/5
Solution:-
The given rational numbers are in form of like fraction,
Hence,
(-3/5)< (-2/5) < (-1/5)
(ii) -1/3, -2/9, -4/3
Solution:-
To convert the given rational numbers into like fraction we have to find LCM,
LCM of 3, 9, and 3 is 9
Now,
(-1/3)= [(-1 × 3)/ (3 × 9)] = (-3/9)
(-2/9)= [(-2 × 1)/ (9 × 1)] = (-2/9)
(-4/3)= [(-4 × 3)/ (3 × 3)] = (-12/9)
Clearly,
(-12/9) < (-3/9) < (-2/9)
Hence,
(-4/3) < (-1/3) < (-2/9)
(iii) -3/7, -3/2, -3/4
Solution:-
To convert the given rational numbers into like fraction we have to find LCM,
LCM of 7, 2, and 4 is 28
Now,
(-3/7)= [(-3 × 4)/ (7 × 4)] = (-12/28)
(-3/2)= [(-3 × 14)/ (2 × 14)] = (-42/28)
(-3/4)= [(-3 × 7)/ (4 × 7)] = (-21/28)
Clearly,
(-42/28) < (-21/28) < (-12/28)
Hence,
(-3/2) < (-3/4) < (-3/7)