Exercise 10.4 Page: 202
1. Construct ΔABC, given m ∠A =60o, m ∠B = 30o and AB = 5.8 cm.
Solution:-

Steps of construction:
1. Draw a line segment AB = 5.8 cm.
2. At point A, draw a ray P to making an angle of 60o i.e. ∠PAB = 60o.
3. At point B, draw a ray Q to making an angle of 30o i.e. ∠QBA = 30o.
4. Now the two rays AP and BQ intersect at the point C.
Then, ΔABC is the required triangle.
2. Construct ΔPQR if PQ = 5 cm, m∠PQR = 105o and m∠QRP = 40o.
(Hint: Recall angle-sum property of a triangle).
Solution:-
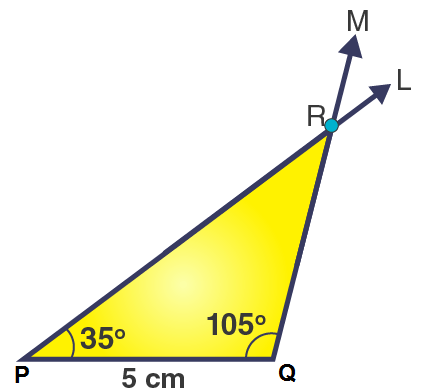
We know that the sum of the angles of a triangle is 180o.
∴ ∠PQR + ∠QRP + ∠RPQ = 180o
= 105o+ 40o+ ∠RPQ = 180o
= 145o + ∠RPQ = 180o
= ∠RPQ = 180o– 1450
= ∠RPQ = 35o
Hence, the measures of ∠RPQ is 35o.
Steps of construction:
1. Draw a line segment PQ = 5 cm.
2. At point P, draw a ray L to making an angle of 105o i.e. ∠LPQ = 35o.
3. At point Q, draw a ray M to making an angle of 40o i.e. ∠MQP = 105o.
4. Now the two rays PL and QM intersect at the point R.
Then, ΔPQR is the required triangle.
3. Examine whether you can construct ΔDEF such that EF = 7.2 cm, m∠E = 110° and
m∠F = 80°. Justify your answer.
Solution:-
From the question it is given that,
EF = 7.2 cm
∠E = 110o
∠F = 80o
Now we have to check whether it is possible to construct ΔDEF from the given values.
We know that the sum of the angles of a triangle is 180o.
Then,
∠D + ∠E + ∠F = 180o
∠D + 110o+ 80o= 180o
∠D + 190o = 180o
∠D = 180o– 1900
∠D = -10o
We may observe that the sum of two angles is 190o is greater than 180o. So, it is not possible to construct a triangle.