अध्याय 1: पूर्णांक Class 7 Maths
CBSE Class 7 Maths Notes Chapter 1 Integers
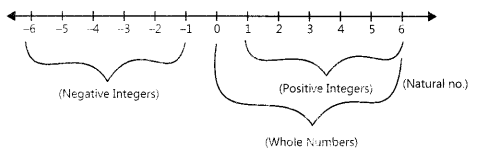
Representation of integers on the number line.
Integers are closed under addition. In general, for any two integers a and b, a + b is an integer.
Integers are closed under subtraction. Thus, if a and b are two integers then a – b is also an integer.
Addition is commutative for integers. In general, for any two integers a and b, we can say a + b = b + a
Subtraction is not commutative for integers.
Addition is associative for integers.
In general for any integers a, b and c, we can say a + (b + c) = (a + b) + c
Zero is an additive identity for integers. In general, for any integer a
a + 0 = a = 0 + a
While multiplying a positive integer and a negative integer, we multiply them as whole numbers and put a minus sign (-) before the product. We thus get a negative integer. In general, for any two positive integers a and b we can say a × (-b) = (-a) × b = -(a × b)
Product of two negative integers is a positive integer. We multiply the two negative integers as whole numbers and put positive sign before the product. In general, for any two positive integers a and b, (-a) × (-b) = a × b
Integers are closed under multiplication. a × b is an integer, for all integers a and b,
Multiplication is commutative for integers. In general, for any two integers a and b, a × b = b × a
The product of a negative integer and zero is zero a × 0 = 0 × a=0
1 is the multiplicative identity for integers.
a × 1 = 1 × a = a
Multiplication is associative for integers, (a × b) × c = a × (b × c)
The distributivity of multiplication over addition is true for integers.
a × (b + c) = a × b + a × c
The distributivity of multiplication over subtraction is true for integers.
a × (b – c) = a × b – a × c
When we divide a positive integer by a negative integer, we first divide them as whole numbers and then put a minus sign (-) before the quotient.
a ÷ (-b) = (-a) ÷ b where b ≠ 0
When we divide a negative integer by a negative integer, we first divide them as whole numbers and then put a positive sign (+).
(-a) ÷ (-b) = a ÷ b where b ≠ 0
Any integer divided by 1 gives the same number.
a ÷ 1 = a
For any integer a, we have a ÷ 0 is not defined.
Natural numbers, whole numbers and integers: The numbers 1, 2, 3,……… which we use for counting are known as natural numbers. The natural numbers along with zero forms the collection of whole numbers.
The numbers……., -3, -2, -1, 0, 1, 2, 3, form the collection of integers.
| Integers | Whole numbers |
| 1. The integers form a bigger group which contains whole numbers and negative numbers. | 1. The whole numbers do not form a group as big as integers because they do not contain negative numbers. |
| 2. The group of integers includes all the whole numbers. | 2. The group of whole numbers does not include all the integers. |
| 3. There is no smallest integer. | 3. 0 is the smallest whole number. |
| 4. Integers are closed under subtraction. | 4. Whole numbers are not closed under subtraction. |
In this chapter, we shall learn more about integers, their properties and operations.
Properties of Addition and Subtraction of Integers
Closure Under Addition
We know that the addition of two whole numbers is again a whole number. For example, 17 + 24 = 41 which is a whole number. This property is known as the closure property for the addition of whole numbers.
This property is true for integers also, i.e., the sum of two integers is always an integer. We cannot find a pair of integers whose addition is not an integer. Since additions of integers give integers, we can say integers are closed under’addition just like whole numbers. In general, for any two integers a and b, a + b is also an integer.
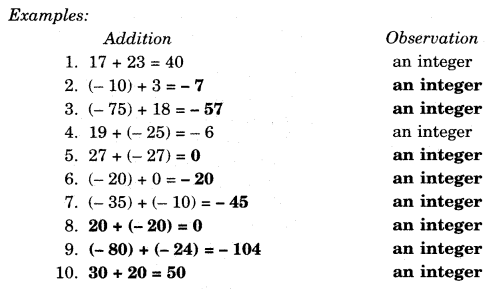
Closure Under Subtraction
If we subtract two integers, then their difference is also an integer. We cannot find any pair of integers whose difference is not an integer. Since subtraction of integers gives integers, we can say integers are closed under subtraction. In general, for any two integers a and b, a – b is also an integer.
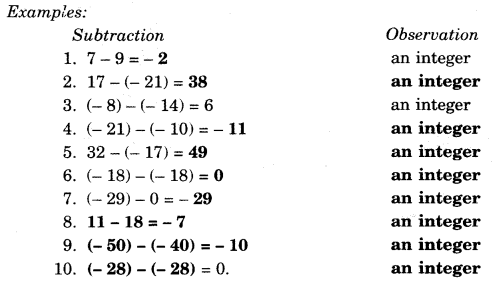
Note: The whole numbers do not satisfy this property.
For example: 5 – 7 = -2 which is not a whole number.
Commutative Property
Commutativity of Addition: We know that 3+ 5 = 5 + 3 = 8, that is, the whole numbers can be added in any order. In other words, addition is commutative for whole numbers. Similarly, the addition is commutative for integers.
We cannot find any pair of integers for which the sum is different when the order is changed. So, we conclude that addition is commutative for integers also. In general, for any two integers a and b, we can say that a + b = b + a.
Commutativity of Subtraction: We know that the subtraction is not commutative for whole numbers.
For example, 10 – 20 = -10 and 20 – 10 = 10
So, 10 – 20 ≠ 20 – 10
Similarly, the subtraction is not commutative for integers.
Associative Property
We cannot find any example for which sum is different when the order of addition is changed. This shows that addition is associative for integers.
In general, for any integers a, b and c, we can say that a + (b + c) = (a + b) + c
Additive Identity
When we add zero to any whole number {i.e., zero and positive integer), we get the same whole number. So, zero is an additive identity for whole numbers. In particular, we can say that zero is an additive identity for positive integers.
Consider the following examples:
(-8) + 0 = -8
(-23) + 0 = -23
0 + (-37) = -37
0 + (-59) = -59
0 + (-43) = -43
-61 + 0 = -61
-50 + 0 = -50
These examples show that zero is an additive identity for negative integers also. Thus, we can say that zero is an additive identity for integers. In general, for any integer a, a + 0 = a = 0 + a
Product of Three or More Negative Integers
We find that if the number of negative integers in a product is even, the product is a positive integer; if the number of negative integers in a product is odd, the product is a negative integer.
Properties of Multiplication of Integers
Closure Under Multiplication
Closure: Let us observe the following table:

We observe that the product of two integers is an integer. We cannot find a pair of integers whose product is not an integer. This gives an idea that the product of two integers is again an integer. So, we say that integers are closed under multiplication. In general, a × b is an integer, for all integers a and b.
Commutativity of Multiplication
We know that multiplication is commutative for whole numbers (i.e., zero and positive
integers). Now, let us observe the following table:

We observe that two integers can be multiplied in any order. The above examples suggest commutativity of multiplication of integers. So, in general, we can say that for any two integers a and b, a × b = b × a.
Multiplication by Zero
We know that any whole number [i.e., zero and positive integers] multiplied by zero gives zero. Let us observe the following table showing the product of a negative integer and zero.
(-3) × 0 = 0
0 × (-4) = 0
(-5) × 0 = 0
0 × (-6) = 0
This table shows that the product of a negative integer and zero is again zero.
In general, for any integer a, a × 0 = 0 × a = 0
Multiplicative Identity
We know that 1 is the multiplicative identity for whole numbers (i.e., zero and positive integers). Let us observe the following table showing the product of a negative integer and 1.
(-3) × 1 = -3
(-4) × 1 = -4
1 × (-5) = -5
1 × (-6) = -6
This table shows that 1 is the multiplicative identity for negative integers also. In general, for any integer a, we have,
a × 1 = 1 × a = a
Multiplication with (-1): Let us observe the following table showing the product of an integer and (-1).
(-3) × (-1) = 3
3 × (-1) = – 3
(-6) × (-1) = 6
(-1) × 13 = -13
(-1) × (-25) = 25
18 × (-1) = -18.
This table shows that (-1) is not the multiplicative identity for integers because when we multiply an integer with (-1) or (-1) with an integer, the result is the integer with the sign changed, i.e., we do not get the same integer. Therefore, for any integer a, we have, a × (-1) = (-1) × a = -a ≠ a
Note: 0 is the additive identity whereas 1 is the multiplicative identity for integers. We get additive inverse of an integer a when we multiply (-1) to a,
i.e., a × (-1) = (-1) × a = -a.
Associativity for Multiplication
Take the integer (- 3). Multiply it with (- 2) to get 6, i.e., (-3) × (-2) = 6.
Then, multiply the product 6 with 5 to get 30, i.e., [(-3) × (-2)] × 5 = 6 × 5 = 30.
Also, (-2) × 5 = (-10).
Multiply integer (-3) with (-10) to get 30.
i.e., (-3) × [(-2) × 5] = (-3) × (-10) = 30.
So, we get the same answer in both the processes, i.e., we get [(-3) × (-2)] × 5 = (-3) × [(-2) × 5]
We observe that the arrangement of integers does not affect the product of integers.
In general, for any three integers a, b and c, (a × b) × c = a × (b × c)
Thus, like whole numbers, the product of three integers does not depend upon the arrangement of integers and this is called associative property for multiplication of integers.
Distributive Property
(i) Distributivity of Multiplication Over Addition: We know that the property of distributivity of multiplication over addition is true for whole numbers.
For example: 16 × (10 + 2) = (16 × 10) + (16 × 2).
(ii) Distributivity of Multiplication Over Subtraction: We know that the property of distributivity of multiplication over subtraction is true for whole numbers (i.e. zero and positive integers).
For example: 4 × (3 – 8) = 4 × 3 – 4 × 8
This property is also true for integers.
For example:
(-9) × [10-(-3)] = (-9) × 13 = -117
and, -9 × 10 – (-9) × (-3) = -90 – 27 = -117
So, (-9) × [10-(-3)]=(-9) × 10 – (-9) × (-3).
We find that these are also equal.
In general, for any three integers a, b and c, a × (b – c) = a × b – a × c.
Division of Integers
1. The division is the inverse operation of multiplication.

Observing the entries in the above table, we find that
- When we divide a negative integer by a positive integer, we get a negative integer.
- When we divide a positive integer by a negative integer, we get a negative integer.
- When we divide a negative integer by a negative integer, we get a positive integer.
2. Division of a negative integer by a positive integer
We observe that
(-12) ÷ 6 = -2 = -(12 ÷ 6)
(-32) ÷ 4 = -8 = -(32 ÷ 4)
(-45) ÷ 5 = -9 = -(45 ÷ 5)
(-12) ÷ 2 = -6 = -(12 ÷ 2)
(- 20) ÷ 5 = -4 = -(20 ÷ 5)
So, we find that while dividing a negative integer by a positive integer, we divide them as whole numbers and put a minus sign (-) before the quotient (i.e. we get a negative integer).
3. Division of a positive integer by a negative integer
We also observe that
72 ÷ (- 8) = -9 = – (72 ÷ 8)
21 ÷ 7 = -3 = -(27 ÷ 7)
This shows that while dividing a positive integer by a negative integer, we divide them as whole numbers and put a minus sign (-) before the quotient (i.e., we get a negative integer).
4. If the dividend and divisor are of opposite sign, then the quotient is negative integer.
Wehave, (—48) ÷ 8= -(48 ÷ 8) = -6
(48) ÷ (-8) = -(48÷8) = -6
So, (-48) ÷ 8 = -6 = 48 ÷ (-8)
5. Division of a negative integer by a negative integer
Lastly we observe that
(-20) ÷ (-4) = 5 = 20 ÷ 4
(-12) ÷ (-6) = 2 = 12 ÷ 6
(-32) ÷ (-8) = 4 = 32 ÷ 8
(-45) ÷ (-9) = 5 = 45 ÷ 9
Here, we notice that while dividing a negative integer by a negative integer, we divide them as whole numbers and put a positive sign i.e. we get a positive integer. We can say that if dividend and divisor are of same signs, then the quotient is a positive integer.
Properties of Division of Integers
(i) Closure: We know that integers are closed under addition, subtraction and multiplication. However, the integers are not closed under division. It can be observed from the following table:
(ii) Commutativity: We know that division is not commutative for whole numbers. For example 16 ÷ 4 ≠ 4 ÷ 16.
Similarly, the division is not commutative for integers.
Note: The division is commutative for integers when the dividend and divisor are equal.
(iii) Like whole numbers, any integer divided by zero is meaningless and zero divided by any integer (other than zero) is equal to zero, i.e., for any integer a, a + 0 is not defined but 0 ÷ a (≠0) = 0.
(iv) When we divide a whole number (i.e., zero and positive integers) by 1, it gives the same whole number.
It is true for negative integers also. For example:
(-8) ÷ 1 = -8
(-11) ÷ 1 = -11
These examples show that negative integer divided by one gives the same negative integer. So, any integer divided by 1 gives the same integer. In general, we can say that for any integer a, a ÷ 1 = a.