1. PQR is a triangle, right-angled at P. If PQ = 10 cm and PR = 24 cm, find QR.

Solution:-

Let us draw a rough sketch of right-angled triangle

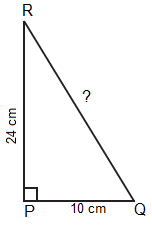
By the rule of Pythagoras Theorem,

Pythagoras theorem states that for any right angled triangle, the area of the square on the hypotenuse is equal to the sum of the areas of square on the legs.

In the above figure RQ is the hypotenuse,

QR² = PQ² + PR²

QR² = 10² + 24²

QR² = 100 + 576

QR² = 676

QR = √676

QR = 26 cm

Hence, the length of the hypotenuse QR = 26 cm.

2. ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.

Solution:-

Let us draw a rough sketch of right-angled triangle

By the rule of Pythagoras Theorem,

Pythagoras theorem states that for any right angled triangle, the area of the square on the hypotenuse is equal to the sum of the areas of square on the legs.

In the above figure RQ is the hypotenuse,

AB² = AC² + BC²

25² = 7² + BC²

625 = 49 + BC²

By transposing 49 from RHS to LHS it becomes – 49

BC² = 625 – 49

BC² = 576

BC = √576

BC = 24 cm

Hence, the length of the BC = 24 cm.

3. A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Solution:-

By the rule of Pythagoras Theorem,

Pythagoras theorem states that for any right angled triangle, the area of the square on the hypotenuse is equal to the sum of the areas of square on the legs.

In the above figure RQ is the hypotenuse,

15² = 12² + a²

225 = 144 + a²

By transposing 144 from RHS to LHS it becomes – 144

a² = 225 – 144

a² = 81

a = √81

a = 9 m

Hence, the length of a = 9 m.

4. Which of the following can be the sides of a right triangle?

(i) 2.5 cm, 6.5 cm, 6 cm.

(ii) 2 cm, 2 cm, 5 cm.

(iii) 1.5 cm, 2cm, 2.5 cm.

In the case of right-angled triangles, identify the right angles.

Solution:-

(i) Let a = 2.5 cm, b = 6.5 cm, c = 6 cm

Let us assume the largest value is the hypotenuse side i.e. b = 6.5 cm.

Then, by Pythagoras theorem,

b² = a² + c²

6.5² = 2.5² + 6²

42.25 = 6.25 + 36

42.25 = 42.25

The sum of square of two side of triangle is equal to the square of third side,

∴The given triangle is right-angled triangle.

Right angle lies on the opposite of the greater side 6.5 cm.

(ii) Let a = 2 cm, b = 2 cm, c = 5 cm

Let us assume the largest value is the hypotenuse side i.e. c = 5 cm.

Then, by Pythagoras theorem,

c² = a² + b²

5² = 2² + 2²

25 = 4 + 4

25 ≠ 8

The sum of square of two side of triangle is not equal to the square of third side,

∴The given triangle is not right-angled triangle.

(iii) Let a = 1.5 cm, b = 2 cm, c = 2.5 cm

Let us assume the largest value is the hypotenuse side i.e. b = 2.5 cm.

Then, by Pythagoras theorem,

b² = a² + c²

2.5² = 1.5² + 2²

6.25 = 2.25 + 4

6.25 = 6.25

The sum of square of two side of triangle is equal to the square of third side,

∴The given triangle is right-angled triangle.

Right angle lies on the opposite of the greater side 2.5 cm.

5. A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.

Solution:-

Let ABC is the triangle and B is the point where tree is broken at the height 5 m from the ground.

Tree top touches the ground at a distance of AC = 12 m from the base of the tree,

By observing the figure we came to conclude that right angle triangle is formed at A.

From the rule of Pythagoras theorem,

BC² = AB² + AC²

BC² = 5² + 12²

BC² = 25 + 144

BC² = 169

BC = √169

BC = 13 m

Then, the original height of the tree = AB + BC

= 5 + 13

= 18 m

6. Angles Q and R of a ΔPQR are 25^o and 65^o.

Write which of the following is true:

(i) PQ² + QR² = RP²

(ii) PQ² + RP² = QR²

(iii) RP² + QR² = PQ²

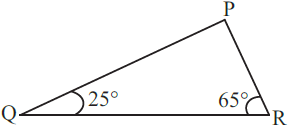
Solution:-

Given that ∠Q = 25^o, ∠R = 65^o

Then, ∠P =?

We know that sum of the three interior angles of triangle is equal to 180^o.

∠PQR + ∠QRP + ∠RPQ = 180^o

25^o + 65^o + ∠RPQ = 180^o

90^o + ∠RPQ = 180^o

∠RPQ = 180 – 90

∠RPQ = 90^o

Also, we know that side opposite to the right angle is the hypotenuse.

∴ QR² = PQ² + PR²

Hence, (ii) is true

7. Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.

Solution:-

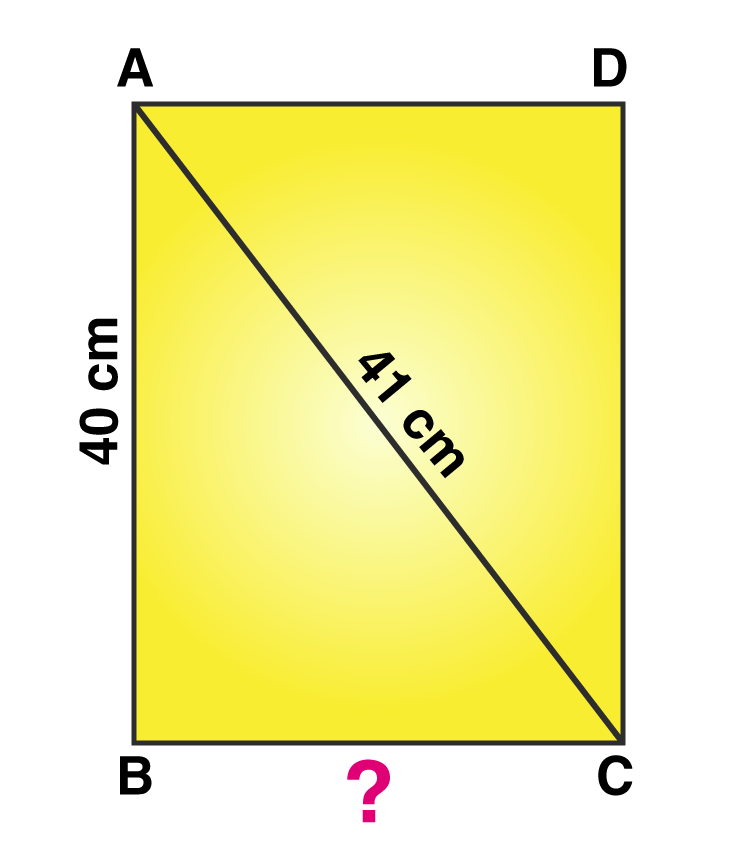
Let ABCD be the rectangular plot.

Then, AB = 40 cm and AC = 41 cm

BC =?

According to Pythagoras theorem,

From right angle triangle ABC, we have:

= AC² = AB² + BC²

= 41² = 40² + BC²

= BC² = 41² – 40²

= BC² = 1681 – 1600

= BC² = 81

= BC = √81

= BC = 9 cm

Hence, the perimeter of the rectangle plot = 2 (length + breadth)

Where, length = 40 cm, breadth = 9 cm

Then,

= 2(40 + 9)

= 2 × 49

= 98 cm

8. The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.

Solution:-

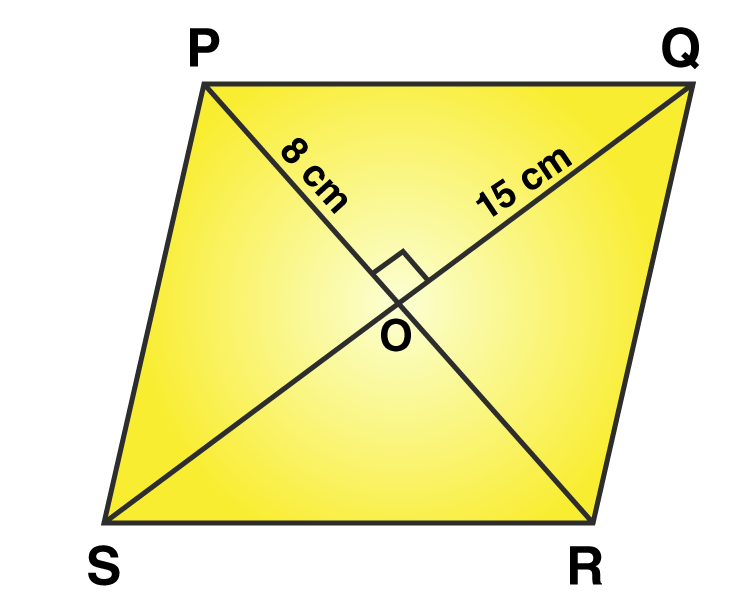
Let PQRS be a rhombus, all sides of rhombus has equal length and its diagonal PR and SQ are intersecting each other at a point O. Diagonals in rhombus bisect each other at 90^o.

So, PO = (PR/2)

= 16/2

= 8 cm

And, SO = (SQ/2)

= 30/2

= 15 cm

Then, consider the triangle POS and apply the Pythagoras theorem,

PS² = PO² + SO²

PS² = 8² + 15²

PS² = 64 + 225

PS² = 289

PS = √289

PS = 17 cm

Hence, the length of side of rhombus is 17 cm

Now,

Perimeter of rhombus = 4 × side of the rhombus

= 4 × 17

= 68 cm

∴ Perimeter of rhombus is 68 cm.