Exercise 10.5 Page: 203
1. Construct the Construct the right angled ΔPQR, where m∠Q = 90°, QR = 8cm and
PR = 10 cm.
Solution:-
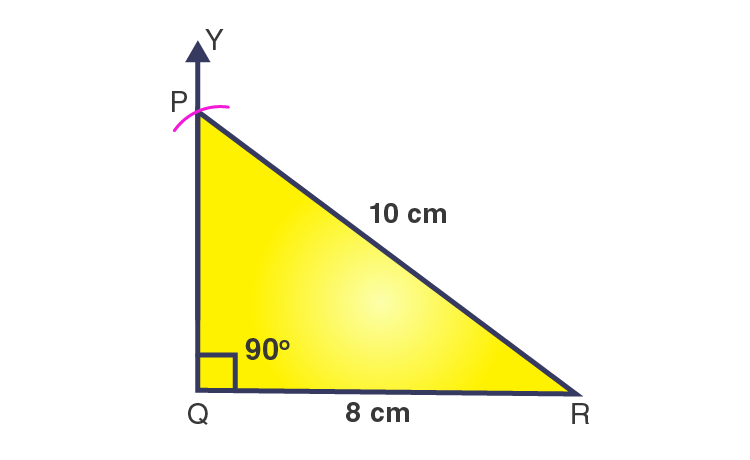
Steps of construction:
1. Draw a line segment QR = 8 cm.
2. At point Q, draw a ray QY to making an angle of 90o i.e. ∠YQR = 90o.
3. With R as a center and radius 10 cm, draw an arc that cuts the ray QY at P.
4. Join PR.
Then, ΔPQR is the required right angled triangle.
2. Construct a right-angled triangle whose hypotenuse is 6 cm long and one of the legs is 4 cm long
Solution:-
Let us consider ΔABC is a right angled triangle at ∠B = 90o
Then,
AC is hypotenuse = 6 cm … [given in the question]
BC = 4 cm
Now, we have to construct the right angled triangle by the above values
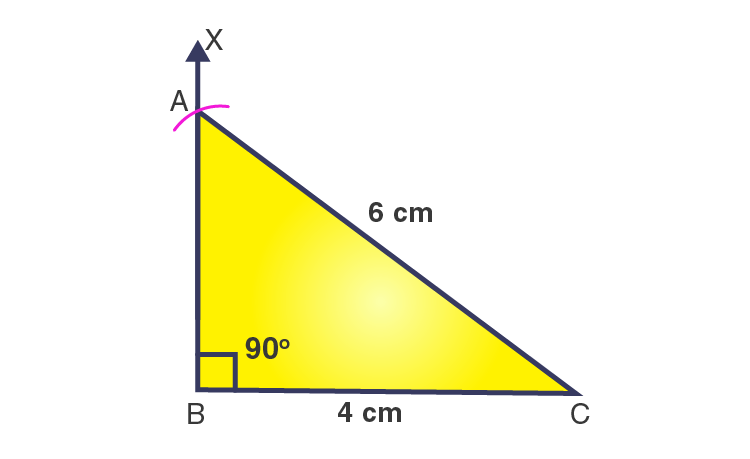
Steps of construction:
1. Draw a line segment BC = 4 cm.
2. At point B, draw a ray BX to making an angle of 90o i.e. ∠XBC = 90o.
3. With C as a center and radius 6 cm, draw an arc that cuts the ray BX at A.
4. Join AC.
Then, ΔABC is the required right angled triangle.
3. Construct an isosceles right-angled triangle ABC, where m∠ACB = 90° and
AC = 6 cm.
Solution:-
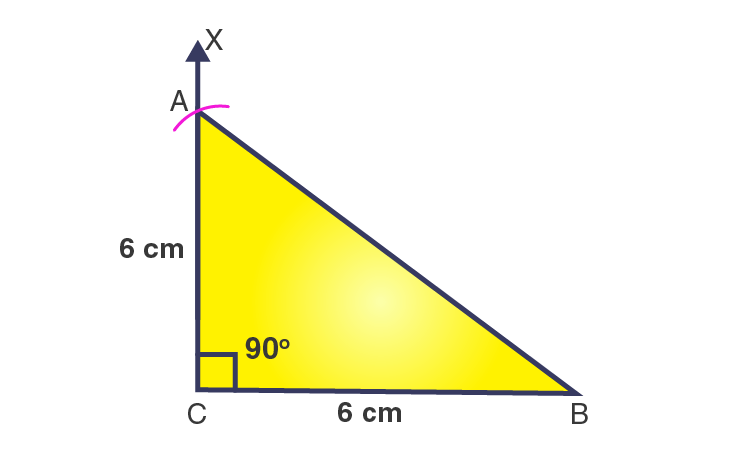
Steps of construction:
1. Draw a line segment BC = 6 cm.
2. At point C, draw a ray CX to making an angle of 90o i.e. ∠XCB = 90o.
3. With C as a center and radius 6 cm, draw an arc that cuts the ray CX at A.
4. Join AB.
Then, ΔABC is the required right angled triangle.