Introduction to Algebraic Expressions

Constant

Constant is a quantity which has a fixed value.

Terms of Expression

Parts of an expression which are formed separately first and then added are known as terms. They are added to form expressions.

Example: Terms 4x and 5 are added to form the expression (4x +5).

Coefficient of a term

The numerical factor of a term is called coefficient of the term.
Example: 10 is the coefficient of the term 10xy in the expression 10xy+4y.

Writing Number patterns and rules related to them

• If a natural number is denoted by n, its successor is (n + 1).
  Example: Successor of n=10 is n+1 =11.
• If a natural number is denoted by n, 2n is an even number and (2n+1) an odd number.
  Example: If n=10, then 2n = 20 is an even number and 2n+1 = 21 is an odd number.

Writing Number patterns and rules related to them

• If a natural number is denoted by n, its successor is (n + 1).
  Example: Successor of n=10 is n+1 =11.
• If a natural number is denoted by n, 2n is an even number and (2n+1) an odd number.
  Example: If n=10, then 2n = 20 is an even number and 2n+1 = 21 is an odd number.

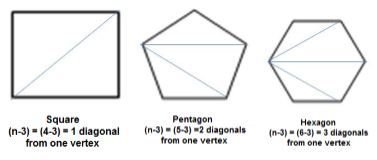
Writing Patterns in Geometry

• Algebraic expressions are used in writing patterns followed by geometrical figures.
  Example: Number of diagonals we can draw from one vertex of a polygon of n sides is (n – 3).

Definition of Variables

• Any algebraic expression can have any number of variables and constants.

  • Variable

    • A variable is a quantity that is prone to change with the context of the situation.
    • a,x,p,… are used to denote variables.

• • Constant

• It is a quantity which has a fixed value.
• In the expression 5x+4, the variable here is x and the constant is 4.
• The value 5x and 4 are also called terms of expression.
• In the term 5x, 5 is called the coefficient of x. Coefficients are any numerical factor of a term.

Factors of a term

Factors of a term are quantities which can not be further factorised. A term is a product of its factors.
Example: The term –3xy is a product of the factors –3, x and y.

Formation of Algebraic Expressions

• Variables and numbers are used to construct terms.
• These terms along with a combination of operators constitute an algebraic expression.
• The algebraic expression has a value that depends on the values of the variables.
• For example, let 6p²−3p+5 be an algebraic expression with variable p
  The value of the expression when p=2 is,
  6(2)² − 3(2) + 5
  ⇒ 6(4) − 6 + 5 = 23
  The value of the expression when p=1 is,
  6(1)² − 3(1) + 5
  ⇒ 6 − 3 + 5 = 8

Like and Unlike Terms

Like terms

• Terms having same algebraic factors are like terms.
  Example: 8xy and 3xy are like terms.

Unlike terms

• Terms having different algebraic factors are unlike terms.
  Example: 7xy and −3x are unlike terms.

Monomial, Binomial, Trinomial and Polynomial Terms

Types of expressions based on the number of terms

Based on the number of terms present, algebraic expressions are classified as:

• Monomial: An expression with only one term.
  Example: 7xy, −5m, etc.
• Binomial: An expression which contains two, unlike terms.
  Example: 5mn+4, x+y, etc
• Trinomial: An expression which contains three terms.
  Example: x+y+5, a+b+ab, etc.

Polynomials

• An expression with one or more terms.
  Example: x+y, 3xy+6+y, etc.

Addition and Subtraction of Algebraic Equations

• Mathematical operations like addition and subtraction can be applied to algebraic terms.
• For adding or subtracting two or more algebraic expression, like terms of both the expressions are grouped together and unlike terms are retained as it is.
• Sum of two or more like terms is a like term with a numerical coefficient equal to the sum of the numerical coefficients of all like terms.
• Difference between two like terms is a like term with a numerical coefficient equal to the difference between the numerical coefficients of the two like terms.
• For example, 2y + 3x − 2x + 4y
  ⇒ x(3−2) + y(2+4)
  ⇒ x+6y
• Summation of algebraic expressions can be done in two ways:
  Consider the summation of the algebraic expressions 5a²+7a+2ab and 7a²+9a+11b
• Horizontal method
  5a²+7a+2ab+7a²+9a+11b
  = (5+7)a²+(7+9)a+2ab+11b
  = 12a²+16a+2ab+11b
• Vertical method
  5a²+7a+2ab
  7a²+9a+11b

Addition and Subtraction of Algebraic Equations

• Mathematical operations like addition and subtraction can be applied to algebraic terms.
• For adding or subtracting two or more algebraic expression, like terms of both the expressions are grouped together and unlike terms are retained as it is.
• Sum of two or more like terms is a like term with a numerical coefficient equal to the sum of the numerical coefficients of all like terms.
• Difference between two like terms is a like term with a numerical coefficient equal to the difference between the numerical coefficients of the two like terms.
• For example, 2y + 3x − 2x + 4y
  ⇒ x(3−2) + y(2+4)
  ⇒ x+6y
• Summation of algebraic expressions can be done in two ways:
  Consider the summation of the algebraic expressions 5a²+7a+2ab and 7a²+9a+11b
• Horizontal method
  5a²+7a+2ab+7a²+9a+11b
  = (5+7)a²+(7+9)a+2ab+11b
  = 12a²+16a+2ab+11b
• Vertical method
  5a²+7a+2ab
  7a²+9a+11b
  ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  12a²+16a+2ab+11b

Use of algebraic expressions in the formula of the perimeter of figures

Algebraic expressions can be used in formulating perimeter of figures.
Example: Let l be the length of one side then the perimeter of:
Equilateral triangle = 3l
Square = 4l
Regular pentagon = 5l

Use of algebraic expressions in formula of area of figures

Algebraic expressions can be used in formulation area of figures.
Example: Let l be the length and b be the breadth then the area of:
Square = l²
Rectangle = l×b = lb
Triangle = b×h/2, where b and h are base and height, respectively.