Exercise 12.1 Page: 234
1. Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.
(i) Subtraction of z from y.
Solution:-
= Y – z
(ii) One-half of the sum of numbers x and y.
Solution:-
= ½ (x + y)
= (x + y)/2
(iii) The number z multiplied by itself.
Solution:-
= z × z
= z2
(iv) One-fourth of the product of numbers p and q.
Solution:-
= ¼ (p × q)
= pq/4
(v) Numbers x and y both squared and added.
Solution:-
= x2 + y2
(vi) Number 5 added to three times the product of numbers m and n.
Solution:-
= 3mn + 5
(vii) Product of numbers y and z subtracted from 10.
Solution:-
= 10 – (y × z)
= 10 – yz
(viii) Sum of numbers a and b subtracted from their product.
Solution:-
= (a × b) – (a + b)
= ab – (a + b)
2. (i) Identify the terms and their factors in the following expressions
Show the terms and factors by tree diagrams.
(a) x – 3
Solution:-
Expression: x – 3
Terms: x, -3
Factors: x; -3

b) 1 + x + x2
Solution:-
Expression: 1 + x + x2
Terms: 1, x, x2
Factors: 1; x; x,x

(c) y – y3
Solution:-
Expression: y – y3
Terms: y, -y3
Factors: y; -y, -y, -y

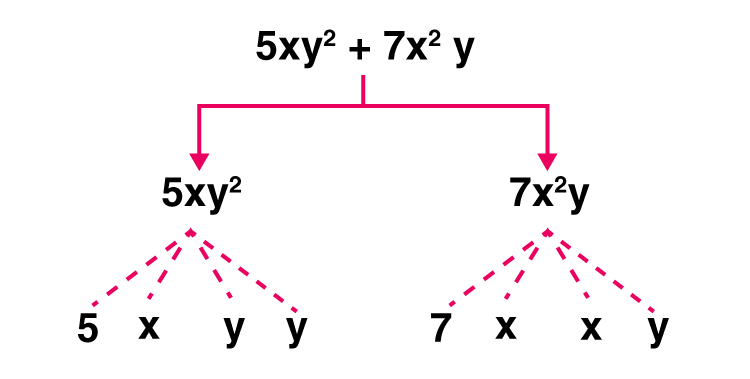
(d) 5xy2 + 7x2y
Solution:-
Expression: 5xy2 + 7x2y
Terms: 5xy2, 7x2y
Factors: 5, x, y, y; 7, x, x, y
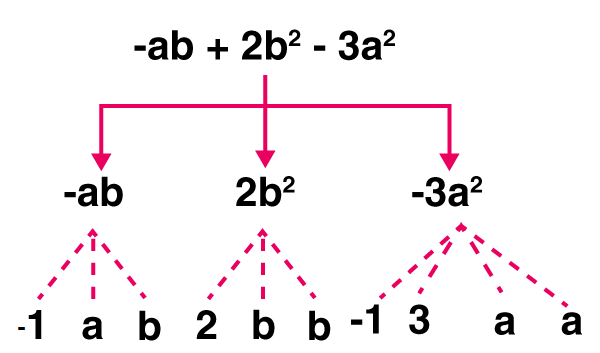
(e) – ab + 2b2 – 3a2
Solution:-
Expression: -ab + 2b2 – 3a2
Terms: -ab, 2b2, -3a2
Factors: -a, b; 2, b, b; -3, a, a
(ii) Identify terms and factors in the expressions given below:
(a) – 4x + 5 (b) – 4x + 5y (c) 5y + 3y2 (d) xy + 2x2y2
(e) pq + q (f) 1.2 ab – 2.4 b + 3.6 a (g) ¾ x + ¼
(h) 0.1 p2 + 0.2 q2
Solution:-
Expressions is defined as, numbers, symbols and operators (such as +. – , × and ÷) grouped together that show the value of something.
In algebra a term is either a single number or variable, or numbers and variables multiplied together. Terms are separated by + or – signs or sometimes by division.
Factors is defined as, numbers we can multiply together to get another number.
| Sl.No. | Expression | Terms | Factors |
| (a) | – 4x + 5 | -4x
5 |
-4, x
5 |
| (b) | – 4x + 5y | -4x
5y |
-4, x
5, y |
| (c) | 5y + 3y2 | 5y
3y2 |
5, y
3, y, y |
| (d) | xy + 2x2y2 | xy
2x2y2 |
x, y
2, x, x, y, y |
| (e) | pq + q | pq
q |
P, q
Q |
| (f) | 1.2 ab – 2.4 b + 3.6 a | 1.2ab
-2.4b 3.6a |
1.2, a, b
-2.4, b 3.6, a |
| (g) | ¾ x + ¼ | ¾ x
¼ |
¾, x
¼ |
| (h) | 0.1 p2 + 0.2 q2 | 0.1p2
0.2q2 |
0.1, p, p
0.2, q, q |
3. Identify the numerical coefficients of terms (other than constants) in the following expressions:
(i) 5 – 3t2 (ii) 1 + t + t2 + t3 (iii) x + 2xy + 3y (iv) 100m + 1000n (v) – p2q2 + 7pq (vi) 1.2 a + 0.8 b (vii) 3.14 r2 (viii) 2 (l + b)
(ix) 0.1 y + 0.01 y2
Solution:-
Expressions is defined as, numbers, symbols and operators (such as +. – , × and ÷) grouped together that show the value of something.
In algebra a term is either a single number or variable, or numbers and variables multiplied together. Terms are separated by + or – signs or sometimes by division.
A coefficient is a number used to multiply a variable (2x means 2 times x, so 2 is a coefficient) Variables on their own (without a number next to them) actually have a coefficient of 1 (x is really 1x)
| Sl.No. | Expression | Terms | Coefficients |
| (i) | 5 – 3t2 | – 3t2 | -3 |
| (ii) | 1 + t + t2 + t3 | t
t2 t3 |
1
1 1 |
| (iii) | x + 2xy + 3y | x
2xy 3y |
1
2 3 |
| (iv) | 100m + 1000n | 100m
1000n |
100
1000 |
| (v) | – p2q2 + 7pq | -p2q2
7pq |
-1
7 |
| (vi) | 1.2 a + 0.8 b | 1.2a
0.8b |
1.2
0.8 |
| (vii) | 3.14 r2 | 3.142 | 3.14 |
| (viii) | 2 (l + b) | 2l
2b |
2
2 |
| (ix) | 0.1 y + 0.01 y2 | 0.1y
0.01y2 |
0.1
0.01 |
4. (a) Identify terms which contain x and give the coefficient of x.
(i) y2x + y (ii) 13y2 – 8yx (iii) x + y + 2
(iv) 5 + z + zx (v) 1 + x + xy (vi) 12xy2 + 25
(vii) 7x + xy2
Solution:-
| Sl.No. | Expression | Terms | Coefficient of x |
| (i) | y2x + y | y2x | y2 |
| (ii) | 13y2 – 8yx | – 8yx | -8y |
| (iii) | x + y + 2 | x | 1 |
| (iv) | 5 + z + zx | x
zx |
1
z |
| (v) | 1 + x + xy | xy | y |
| (vi) | 12xy2 + 25 | 12xy2 | 12y2 |
| (vii) | 7x + xy2 | 7x
xy2 |
7
y2 |
(b) Identify terms which contain y2 and give the coefficient of y2.
(i) 8 – xy2 (ii) 5y2 + 7x (iii) 2x2y – 15xy2 + 7y2
Solution:-
| Sl.No. | Expression | Terms | Coefficient of y2 |
| (i) | 8 – xy2 | – xy2 | – x |
| (ii) | 5y2 + 7x | 5y2 | 5 |
| (iii) | 2x2y – 15xy2 + 7y2 | – 15xy2
7y2 |
– 15x
7 |
5. Classify into monomials, binomials and trinomials.
(i) 4y – 7z
Solution:-
Binomial.
An expression which contains two unlike terms is called a binomial.
(ii) y2
Solution:-
Monomial.
An expression with only one term is called a monomial.
(iii) x + y – xy
Solution:-
Trinomial.
An expression which contains three terms is called a trinomial.
(iv) 100
Solution:-
Monomial.
An expression with only one term is called a monomial.
(v) ab – a – b
Solution:-
Trinomial.
An expression which contains three terms is called a trinomial.
(vi) 5 – 3t
Solution:-
Binomial.
An expression which contains two unlike terms is called a binomial.
(vii) 4p2q – 4pq2
Solution:-
Binomial.
An expression which contains two unlike terms is called a binomial.
(viii) 7mn
Solution:-
Monomial.
An expression with only one term is called a monomial.
(ix) z2 – 3z + 8
Solution:-
Trinomial.
An expression which contains three terms is called a trinomial.
(x) a2 + b2
Solution:-
Binomial.
An expression which contains two unlike terms is called a binomial.
(xi) z2 + z
Solution:-
Binomial.
An expression which contains two unlike terms is called a binomial.
(xii) 1 + x + x2
Solution:-
Trinomial.
An expression which contains three terms is called a trinomial.
6. State whether a given pair of terms is of like or unlike terms.
(i) 1, 100
Solution:-
Like term.
When term have the same algebraic factors, they are like terms.
(ii) –7x, (5/2)x
Solution:-
Like term.
When term have the same algebraic factors, they are like terms.
(iii) – 29x, – 29y
Solution:-
Unlike terms.
The terms have different algebraic factors, they are unlike terms.
(iv) 14xy, 42yx
Solution:-
Like term.
When term have the same algebraic factors, they are like terms.
(v) 4m2p, 4mp2
Solution:-
Unlike terms.
The terms have different algebraic factors, they are unlike terms.
(vi) 12xz, 12x2z2
Solution:-
Unlike terms.
The terms have different algebraic factors, they are unlike terms.
7. Identify like terms in the following:
(a) – xy2, – 4yx2, 8x2, 2xy2, 7y, – 11x2, – 100x, – 11yx, 20x2y, – 6x2, y, 2xy, 3x
Solution:-
When term have the same algebraic factors, they are like terms.
They are,
– xy2, 2xy2
– 4yx2, 20x2y
8x2, – 11x2, – 6x2
7y, y
– 100x, 3x
– 11yx, 2xy
(b) 10pq, 7p, 8q, – p2q2, – 7qp, – 100q, – 23, 12q2p2, – 5p2, 41, 2405p, 78qp,
13p2q, qp2, 701p2
Solution:-
When term have the same algebraic factors, they are like terms.
They are,
10pq, – 7qp, 78qp
7p, 2405p
8q, – 100q
– p2q2, 12q2p2
– 23, 41
– 5p2, 701p2
13p2q, qp2