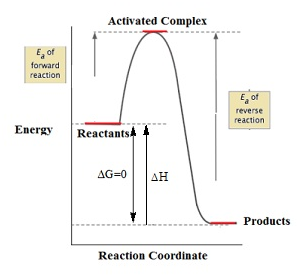
Activation energy

• The minimum quantitiy of external energy required for the conversion of reactant into product or to produce an unstable intermediate is called activation energy. It is E  
• Rate of reaction is inversely proportional to the activation energy.
• Therefore, greater value of activation energy leads to lower rate of reaction and increased influence of temperature change on the rate constant.

PROBLEM.   The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate E_Solution. 

SOLUTION.   It is given that T₁ = 298 K

∴T2 = (298 + 10) K

= 308 K

We also know that the rate of the reaction doubles when temperature is increased by 10°.

Therefore, let us take the value of k₁ = k and that of k₂ = 2k

Also, R = 8.314 J K ^{– 1} mol ^{– 1}

Now, substituting these values in the equation:

Log k₂/k₁ = E_a/2.303R [T₂-T₁/T₁T₂]

Log 2k/k = E_a/2.303 X 8.314 [10/298 X 308]

E_a= 2.303 X 8.314 X 298 X 308 X log2/10

= 52897.78 J mol ^{– 1}

= 52.9 kJ mol ^{– 1}

Arrhenius equation

• The formula used to calculate the energy of activation and justify the effect of temperature on rate of reaction is called Arrhenius Equation.
• It is given by the formula,

K = A e^-Ea/RT

Where,

k = Rate constant

A= Frequency factor

e = mathematical quantity

E_a= activation energy

R = gas constant

T = kelvin temperature

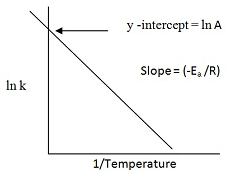
ln K = ln A – Ea/(2.303RT)

Equation of a straight line with slope = –E_a /R.

• When E_a = 0 , Temperature = Infinity

K = Ae⁰ = A

e^-Ea/RT =Boltzmann factor.

• For a chemical reaction the rate constant gets doubled for a rise of 10° temperature. This is because according to Arrhenius Equation,

K = Ae^-Ea/RT

Taking log on both sides of the equation

Ln k = ln A – E_a/RT

Comparing with the equation of a straight line

y= mx+c,  

[m= slope of the line

c= y-intercept]

So we have:

y = ln k

x = 1/T

m = -E_a / R

c = ln A

Plotting k Vs (1/T)

PROBLEM.   Find the activation energy (in kJ/mol) of the reaction if the rate constant at 600K is 3.4 M^-1 s^-1 and 31.0 at 750K.

SOLUTION.   Ln k = ln A – E_a/RT

To find E_a, subtract ln A from both sides and multiply by -RT.

E_a = (ln A – ln k)RT

Collision theory

• It states that:
• According to collision theory the molecules collides with great kinetic energy in order to bring about a chemical reaction.

The molecules of the reacting species collide through the space in a rectilinear motion.

Rate of a chemical reaction is proportional to the number of collisions between the molecules of the reacting species.

The molecules must be properly oriented.

• Rate of successful collisions ∝ Fraction of successful collisions X Overall collision frequency.
• The number of collisions per second per unit volume of the molecules in a chemical reaction is called collision frequency (Z).

Let A+B –> C + D

Rate = Z_ABe^-Ea/RT

Here Z_AB = collision frequency of A and B.

• In many reactions Rate = P Z_ABe^-Ea/RT

Where p= steric factor which takes into account the proper orientation of the molecules participating in a chemical reaction.

PROBLEM.   The activation energy for the reaction 2HI_(g) → H₂ + I_2(g) is 209.5 kJ mol^-1 at 581 K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?

SOLUTION.   E_a = 209.5 kJ mol ^{– 1} = 209500 J mol ^{– 1}

T = 581 K

R = 8.314 JK ^{– 1} mol ^{– 1}

Fraction of molecules of reactants having energy equal to or greater than activation energy is as follows:

x = e^-Ea/RT

ln x = -Ea/RT

log x = Ea/2.303RT

log x = 209500 J mol^-1/2.303 X 8.314 J K^-1 mol^-1 X 581 = 18.8323

x = antilog (18.323)

= antilog 19.1977

= 1.471 X 10^-19