Molecularity

• As we know that molecules need to collide to bring about a chemical reaction, so the number of molecules participating in an elementary chemical reaction that collides to bring about the chemical reaction is called molecularity of a reaction.
• The value of molecularity of a reaction is always a positive value.
• Let us consider a following reaction:

A + 2B –> C + D

Here reactants are: 1 molecule of A ,2 molecules of B

Products are: 1 molecule of C , 1 molecule of D.

Therefore we can conclude that reaction is trimolecular.

 A reaction with molecularity =1 is called unimolecular.

Example, PCl₅ –> PCl₃ + Cl₂

• A reaction with molecularity =2 is called bimolecular.

Example, Cl + CH₄ –> HCl + CH₃

• A reaction with molecularity =3 is called trimolecular.

2FeCl₃ + SnCl₂ –> 2FeCl₂ + SnCl₄

• It is theoretical value and does not determine the rate of reaction. Nor does it depend upon external factors like temperature or pressure, etc.

Integrated rate equation

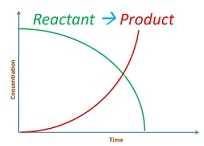
Consider the reaction

aA + bB –> cC + dD

Rate = k [A]^x[B]^y

-dR/dt = k[A]^x[B]^y

dR/dt is instantaneous rate.

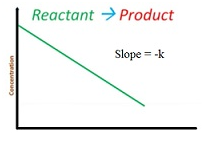
Integrated rate equation for zero order reaction

-dR/dt = k[R]⁰=k

dR/dt = -k

∫ dR = -k ∫ dt

[R]=-kt +I

At t = 0

R₀= -k .0 + I

I = R₀

So the equation becomes R = -kt + R₀

Graph for this is as follows:

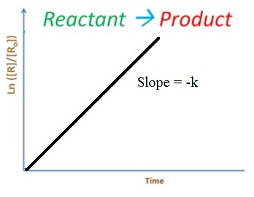
Integrated rate equation for first order reaction

Rate = -dR/dt = k[R]²

 ∫ dR/R= – ∫ kt

ln R = -kt + I

At t = 0

R = R₀

ln R₀=-k X 0 +I

I = ln R₀

So equation becomes

ln R = -kt + ln R₀

ln [R₀/ R]=-kt

Rate law

• The representation of rate of reaction in terms of molar concentration of the reactants participating in a reaction raised to some power is called rate law.
• It is also called rate expression or rate equation.
• Consider a reaction:

2NO (g) + O₂ (g) –> 2NO₂

Rate ∝ [NO]²

Rate ∝ [O₂]

Combining these two rates we derive

Rate ∝ [NO]² [O₂]

Rate =k [NO]² [O₂]

• Where k is the proportionality constant with a definite value at a specific temperature for a specific reaction and is called Rate Constant.
• Rate law expression = -d[R]/ dt = k [NO]² [O₂]

Half life reactions : The time elapsed in reduction of the concentration of a reactant participating in a chemical reaction to one half of its original concentration is called half-life reaction and is represented by t_1/2.

Half-life for zero order reactions:

A –> B

At time t = 0 concentration of A (reactant) is a and B (product) is 0. At time t = t the concentration of A (reactant) is (a-x) and that of B (product) is x.

x = k₀t à a/2 = k₀t_1/2 = a/2k₀

t_1/2 =a/2k₀

a=(2k₀)(t_1/2)

y = mx

t = Independent variable. It is taken at x-axis.

m = 2k₀

Half-life for first order reactions:

t = 2.303/k₁ log a/(a-x)

For half-life x = a/2; t = t _1/2

t _½ = 2.303/k₁ log a/(a-a/2) –> t1/2 = 2.303/k₁ log2

t _½ = 2.303/k₁ X 3.010

t _½ = 0.693/ k₁

Rate determining step

• The slowest step during a chemical reaction determines the overall speed of a reaction towards completion is called rate determining step.
• Let us consider the following reaction,

NO₂(g)+CO(g)→NO(g)+CO₂(g)

• The elementary steps of the reaction are as follows: 

Step 1:   NO₂+NO₂→NO+NO₃ (Rate constant = k₁, slow)

Step 2: NO₃+CO→NO₂+CO₂ (Rate constant = k_2, fast)

• As the first step is the slowest step in the reaction it will determine the rate of the overall reaction. Therefore Step1 is the rate determining step of the given reaction and hence the rate expression for the given reaction is the product of rate constant and the reactants of this step.

Rate = k1[NO₂][NO₂]=k1[NO₂]₂