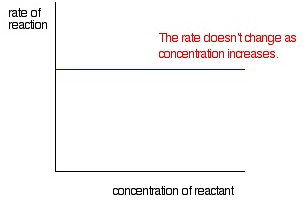
Zeroth order reaction

If the rate of reaction is independent of concentration of the reactant participating in the reaction then the reaction is called Zeroth order reaction.

A –> B

At time t = 0 concentration of A (reactant) is a and B (product) is 0. At time t = t the concentration of A (reactant) is (a-x) and that of B (product) is x.

-d[A]/dt = k₀[A]⁰ => dx/dt = k₀(a-x)⁰

dx/dt = k₀

∫ ₀^x  dx =k₀ ∫₀ ^xdt

X = k₀t

PROBLEM.   The decomposition of NH3on platinum surface is zero order reaction. What are the rates of production of N2and H2if k = 2.5 x 10-4mol-1L s-1?

SOLUTION.    2NH₃  –> N₂ + 3H₂

Rate of zero order reaction

-1/2 (d[NH₃]/dt) = d[N₂]/dt = 1/3 (d[H₂]/dt)

-1/2 (d[NH₃]/dt) = d[N₂]/dt = 1/3 (d[H₂]/dt)= k = 2.5 x 10^-4 mol L^-1 s^-1

Rate of production of N₂

d[N₂]/dt = 2.5 x 10^-4 mol L^-1 s^-1

Rate of production of H₂

d[H₂]/dt = 3 x 2.5 x 10^-4 mol L^-1 s^-1

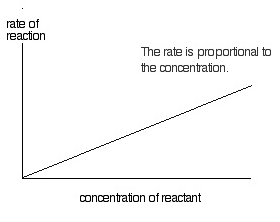
First order reaction

If the rate of reaction depends on the concentration of single reactant participating in chemical reaction raised to the first power then it is called a first order reaction.

A –> B

At time t = 0 concentration of A (reactant) is a and B (product) is 0. At time t = t the concentration of A (reactant) is (a-x) and that of B (product) is x.

-dx/dt ∝ (a-x) = dx/dt = k1(a-x)

∫ 0x  dx/(a-x) = k1∫ 0t dt

 dx/dt = k0(a-x)0

dx/dt = k0

∫0 x dx = k0∫ 0t dt

ln (a/a-x) = k1t => t = 1/ k1 ln (a/a-x) = 2.303/ k1 log (a/a-x)

k1 = 2.303 log (a/a-x)

PROBLEM.   A first order reaction has a rate constant 1.15 10-3s-1. How long will 5 g of this reactant take to reduce to 3 g?

SOLUTION.   From the question, we can write down the following information:

Initial amount = 5 g

Final concentration = 3 g

Rate constant = 1.15 10 – 3s – 1

We know that for a 1st order reaction,

t = (2.303/k)log[R0]/[R]

(2.303/1.15X10-3)log[5]/[3]

(2.303/1.15X10-3) X 0.2219 = 444.38 s = 444 s

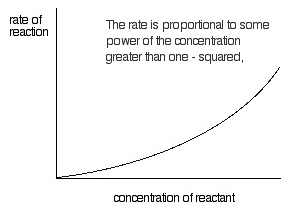
Second order reaction 

A reaction with order equal to two is called a second order reaction.

r = k[A]²

or r = k [A][B]

Pseudo order reaction

The reaction that appears to be an n^th order reaction but belongs to some different order is called Pseudo order reaction.

For example, a pseudo first order reaction is a chemical reaction between two reactants participating in a chemical reaction and therefore should be a second order reaction. But it resembles to be a first order reaction due to the presence of reactants in negligible quantity.

Let R` + R“ –> P

Rate = k[A]¹[B]¹

Order of reaction = 2.

Let us consider another reaction,

CH₃Br + OH⁻→ CH₃OH+Br⁻

Rate law for this reaction is

Rate = k [OH⁻][CH₃Br]

Rate = k [OH⁻][CH₃Br] = k(constant)[CH₃Br]=k′[CH₃Br]

As only the concentration of CH₃Br would change during the reaction, the rate would solely depend upon the changes in the CH₃Br reaction.