Close Packed Structure

In solid, constituent particles are close packed, leaving the minimum vacant space (void).

Close Packing in One Dimension

• The only way to arrange spheres in a one dimensional close packed structure is to arrange the spheres in a single row and touching each other.

• Each sphere is in contact with two of its surrounding atom.
• The number of nearest surrounding particles is called its coordination number. Therefore in one dimensional close packed arrangement, the coordination number is 2.

Formula of a Compound and Number of Voids Filled

• The number of octahedral voids present in a lattice = The number of close packed particles.
• The number of tetrahedral voids produced is twice this number.
• In ionic solids, the bigger ions i.e. anions forms close packed structure and the smaller ions i.e. cations occupy the voids.
• If the latter ion is small then tetrahedral voids are occupied, if bigger, then octahedral voids are occupied.
• In a compound, the fraction of octahedral or tetrahedral voids that are occupied depends upon the chemical formula of the compound.
• Close packed structures have both tetrahedral and octahedral voids.

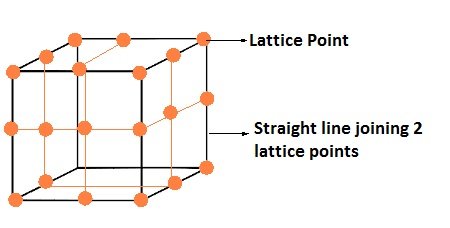
Locating Tetrahedral Voids

• Take a unit cell of ccp or fcc lattice divide into eight small cubes with each small cube having atoms at alternate corners.
• Thus, each small cube has 4 atoms that on joining to each other make a regular tetrahedron.
• Thus, there is one tetrahedral void in each small cube and eight tetrahedral voids in total.
• Each of the eight small cubes have one void in one unit cell of ccp
• ccp structure has 4 atoms per unit cell. Thus, the number of tetrahedral voids is twice the number of atoms.

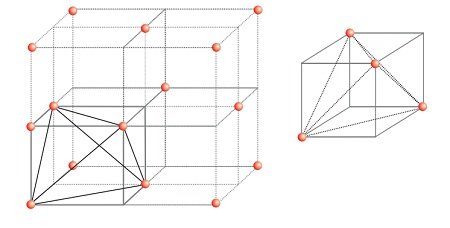
Locating Octahedral Voids

• Take a unit cell of ccp or fcc.
• The body center of the cube, C is not occupied but surrounded by six atoms on face centers.
• Joining the face centers creates a octahedron.
• Thus, this unit cell has one octahedral void at the body centre of the cube.
• There is one octahedral void at the centre of each
  of the 12 edges.
• It is surrounded by six atoms, three belonging to the same unit cell and three belonging to
  two adjacent unit cells.
• Each edge of the cube and octahedral void are shared between four adjacent unit cells.
• Only ¼ of each void belongs to a particular unit cell

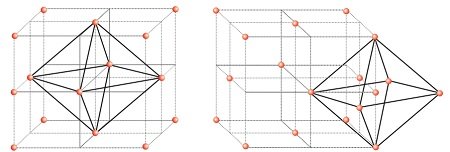
In cubic close packed structure octahedral void at the body-center of the cube = 1
12 octahedral voids positioned at each edge and shared between four unit cells =12 x 1/4 =3

Total number of octahedral voids = 4

In ccp structure, each unit cell has 4 atoms. Thus, the number
of octahedral voids is equal to this number.

Question : If the radius of the octachedral void is r and radius of the atoms in close packing is R, derive relation between r and R.

Answer: Given that

Radius of octahedral void in close packing = r      

Radius of atom in close packing = R                 

Using Pythagoras theorem,

2R² = (R+ r)² + (R+ r)²

4R² = 2(R +r)²

2R² = (R+ r)²

R√2 = R +r

R√2 – R = r

r = R√2 – R

Putting the value of √2, we derive

r = R (1.414-1)

r = 0.414R

Question : A compound forms hexagonal close-packed structure. What is the total number of voids in 0.5 mol of it? How many of these are tetrahedral voids?

Answer: Number of particles in 1 mol of compound = 6.022 X 10²³

Number of particles in 0.5 mol = 0.5 X6.022 X 10²³ = 3.011 X 10²³

Number of octahedral voids = number of atoms or particles.

Number of tetrahedral voids = 2 X number of particles

Therefore number of octahedral in the given compound = 3.011 X 10²³

Number of tetrahedral voids = 2 X 3.011 X 10²³ = 6.022 X 10²³

The total number of voids = 3.011 X 10²³ + 6.022 X 10²³

= 9.033 X 10²³

Number of tetrahedral voids = 6.022 X 10²³

Question. Atoms of element B form hcp lattice and those of the element A occupy 2/3rd of tetrahedral voids. What is the formula of the compound formed by the elements A and B?

Answer: Number of tetrahedral voids = 2 X number of particles of atom B

Number of atoms of A is equal to  of the number of atoms of B.

Hence the ratio A:B = (4/3):1 or 4:3

Therefore,  the formula of the compound is A₄B₃.

Question: A compound is formed by two elements M and N. The element N
forms ccp and atoms of M occupy 1/3rd of tetrahedral voids. What
is the formula of the compound?

Answer: The ccp lattice is made by the atoms of the element N.

Here, the Number of tetrahedral voids = 2 X number of particles of the elements N.

According to the question, the atoms of element M occupy = 1/3^rd of the tetrahedral voids.

Therefore, the number of atoms of M is equal to

 2 x 1/3 = 2/3rd of the number of atoms of N.

Therefore, the ratio M:N = 2/3 :1   = 2:3

Hence formula of the compound is M₂N₃.

1.14. What is the two-dimensional coordination number of a molecule in a square close-packed layer? (NCERT Book)
Ans: In the two-dimensional square close-packed layer, a particular molecule is in contact with four molecules. Hence, the coordination number of the molecule is four.

1.15. A compound forms hexagonal close-packed. structure. What is the total number of voids in 0. 5 mol of it? How many of these are tetrahedral voids? (NCERT Book)
Ans:
No. of atoms in close packings 0.5 mol =0.5 x 6.022 x 10²³ =3.011 x 10²³
No. of octahedral voids = No. of atoms in packing =3.011 x 10²³
No. of tetrahedral voids = 2 x No. of atoms in packing
= 2 x 3.011 x 10²³ = 6.022 x 10²³
Total no. of voids = 3.011 x 10²³ + 6.022 x 10²³
= 9.033 x 10²³

1.16. A compound is formed by two elements M and N. The element N forms ccp and atoms of the element M occupy 1/3 of the tetrahedral voids. What is the formula of the compound? (C.B.S.E. Foreign 2015)(NCERT Book)
Ans: Let us suppose that,
the no. of atoms of N present in ccp = x
Since 1/3rd of the tetrahedral voids are occupied by the atoms of M, therefore,
the no. of tetrahedral voids occupied = 2x/3
The ratio of atoms of N and M in the compound = x : 2x/3 or 3 : 2
∴ The formula of the compound = N₃M₂ or M₂N₃

1.7. How will you distinguish between the following pairs of terms :
(a) Hexagonal close packing and cubic close packing
(b) Crystal lattice and unit cell
(c) Tetrahedral void and octahedral void.
Sol.
(a) In hexagonal close packing (hcp), the spheres of the third layer are vertically above the spheres of the first layer
(ABABAB……. type). On the other hand, in cubic close packing (ccp), the spheres of the fourth layer are present above the spheres of the first layer (ABCABC…..type).
(b) Crystal lattice: It deplicts the actual shape as well as size of the constituent particles in the crystal. It is therefore, called space lattice or crystal lattice.

Question 24. ( The Solid State NCERT Solution )
Aluminium crystallises in a cubic close packed structure. Its metallic radius is 125 pm.

1. What is the length of the side of the unit cell?
2. How many unit cells are there in 1.00 cm³ of aluminium?