NCERT TEXTBOOK QUESTIONS SOLVED
2.1. Calculate the mass percentage of benzene (C6H6) and carbon tetrachloride (CCl4) if 22 g of benzene is dissolved in 122 g of carbon tetrachloride.
Ans: Mass of solution = Mass of C6H6 + Mass of CCl4
= 22 g+122 g= 144 g
Mass % of benzene = 22/144 x 100 =15.28 %
Mass % of CCl4 = 122/144 x 100 = 84.72 %


2.4. Calculate the mass of urea (NH2CONH2) required in making 2.5 kg of 0.25 molal aqueous solution.
Ans: 0.25 Molal aqueous solution to urea means that
moles of urea = 0.25 mole
mass of solvent (NH2CONH2) = 60 g mol-1
.’. 0.25 mole of urea = 0.25 x 60=15g
Mass of solution = 1000+15 = 1015g = 1.015 kg
1.015 kg of urea solution contains 15g of urea
.’. 2.5 kg of solution contains urea =15/1.015 x 2.5 = 37 g









NCERT EXERCISES
2.1. Define the terra solution. How many types of solutions are formed? Write briefly about each type with an example.
Sol: A solution is a homogeneous mixture of two or more chemically non-reacting substances. Types of solutions: There are nine types of solutions.
Types of Solution Examples
Gaseous solutions
(a) Gas in gas Air, mixture of 02 and N2, etc.
(b) Liquid in gas Water vapour
(c) Solid in gas Camphor vapours in N2 gas, smoke etc.
Liquid solutions
(a) Gas in liquid C02 dissolved in water (aerated water), and 02 dissolved in water, etc.
(b) Liquid in liquid Ethanol dissolved in water, etc.
(c) Solid in liquid Sugar dissolved in water, saline water, etc.
Solid solutions
(a) Gas in solid Solution of hydrogen in palladium
(b) Liquid in solid Amalgams, e.g., Na-Hg
(c) Solid in solid Gold ornaments (Cu/Ag with Au)
2.2. Suppose a solid solution is formed between two substances, one whose particles are very large and the other whose particles are very small. What type of solid solution is this likely to be ?
Sol: The solution likely to be formed is interstitial solid solution.
2.3 Define the following terms:
(i) Mole fraction
(ii) Molality
(iii) Molarity
(iv) Mass percentage
Sol: (i) Mole fraction: It is defined as the ratio of the number of moles of the solute to the total number of moles in the solution. If A is the number of moles of solute dissolved in B moles of solvent, then Mole fraction of solute








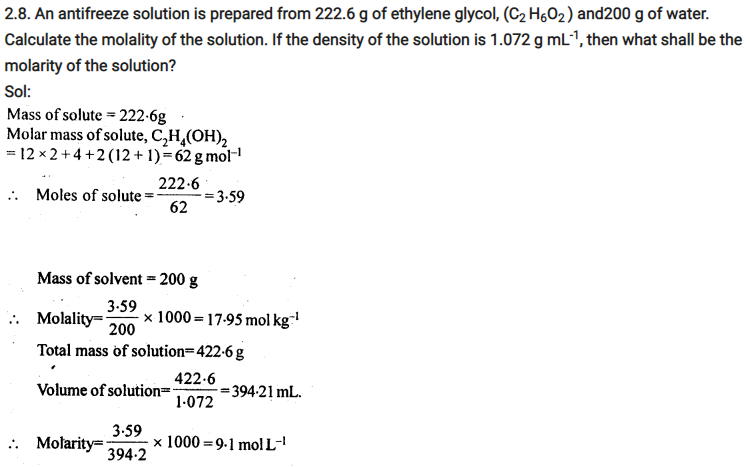
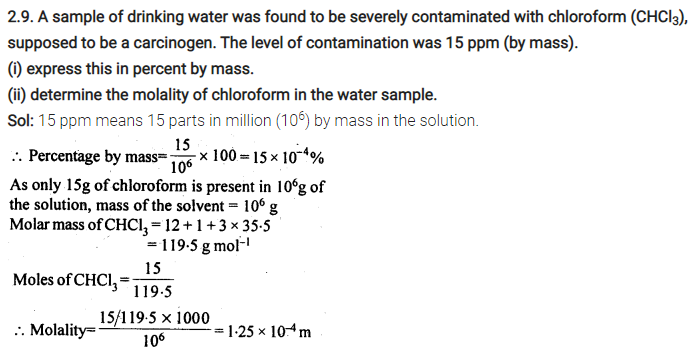
2.10. What role does the molecular interaction play in solution of alcohol in water?
Sol: In case of alcohol as well as water, the molecules are interlinked by intermolecular hydrogen bonding. However, the hydrogen bonding is also present in the molecules of alcohol and water in the solution but it is comparatively less than both alcohol and water. As a result, the magnitude of attractive forces tends to decrease and the solution shows positive deviation from Raoult’s Law. This will lead to increase in vapour pressure of the solution and also decrease in its boiling point.
2.11. Why do gases always tend to be less soluble in liquids as the temperature is raised?
Sol: When gases are dissolved in water, it is accompanied by a release of heat energy, i.e., process is exothermic. When the temperature is increased, according to Lechatlier’s Principle, the equilibrium shifts in backward direction, and thus gases becomes less soluble in liquids.
2.12. State Henry’s law and mention some of its important applications.
Sol:
Henry’s law: The solubility of a gas in a liquid at a particular temperature is directly proportional to the pressure of the gas in equilibrium with the liquid at that temperature.
or
The partial pressure of a gas in vapour phase is proportional to the mole fraction of the gas (x) in the solution. p = KHX
where KH is Henry’s law constant.
Applications of Henry’s law :
(i) In order to increase the solubility of CO2 gas in soft drinks and soda water, the bottles are normally sealed under high pressure. Increase in pressure increases the solubility of a gas in a solvent according to Henry’s Law. If the bottle is opened by removing the stopper or seal, the pressure on the surface of the gas will suddenly decrease. This will cause a decrease in the solubility of the gas in the liquid i.e. water. As a result, it will rush out of the bottle producing a hissing noise or with a fiz.
(ii) As pointed above, oxygen to be used by deep sea divers is generally diluted with helium inorder to reduce or minimise the painfril effects during decompression.
(iii) As the partial pressure of oxygen in air is high, in lungs it combines with haemoglobin to form oxyhaemoglobin. In tissues, the partial pressure of oxygen is comparatively low. Therefore, oxyhaemoglobin releases oxygen in order to carry out cellular activities.
2.13. The partial pressure of ethane over a solution containing 6.56 × 10-3 g of ethane is 1 bar. If the solution contains 5.00 × 10-2 g of ethane, then what shall be the partial pressure of the gas?
Sol:

2.14. According to Raoult’s law, what is meant by positive and negative deviaitions and how is the sign of ∆solH related to positive and negative deviations from Raoult’s law?
Sol: Solutions having vapour pressures more than that expected from Raoult’s law are said to exhibit positive deviation. In these solutions solvent – solute interactions are weaker and ∆solH is positive because stronger A – A or B – B interactions are replaced by weaker A – B interactions. Breaking of the stronger interactions requires more energy & less energy is released on formation of weaker interactions. So overall ∆sol H is positive. Similarly ∆solV is positive i.e. the volume of solution is some what more than sum of volumes of solvent and solute.
So there is expansion in volume on solution formation.
Similarly in case of solutions exhibiting negative deviations, A – B interactions are stronger than A-A&B-B. So weaker interactions are replaced by stronger interactions so , there is release of energy i.e. ∆sol H is negative.
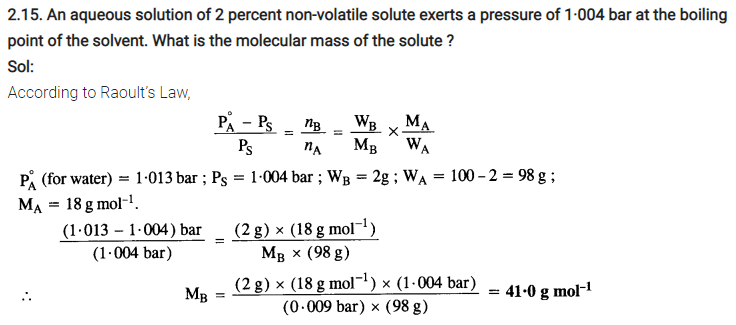





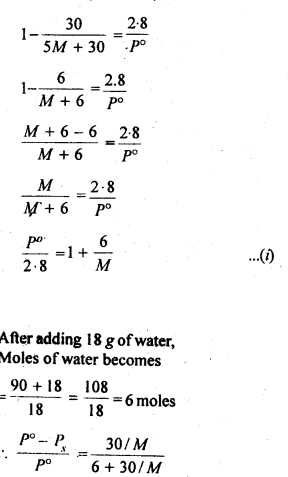
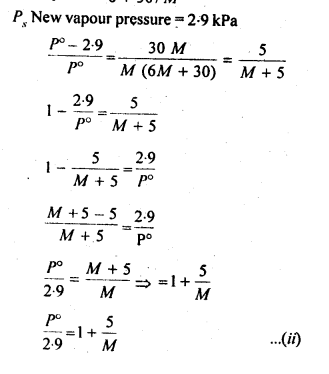





2.24. Based on solute solvent interactions, arrange the following in order of increasing solubility in n-octane and explain. Cyclohexane, KCl, CH3OH, CH3CN.
Sol: n-octane (C8H18) is a non-polar liquid and solubility is governed by the principle that like dissolve like. Keeping this in view, the increasing order of solubility of different solutes is:
KCl < CH3OH < CH3C=N < C6H12 (cyclohexane).
2.25. Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water?
(i) phenol
(ii) toluene
(iii) formic acid
(iv) ethylene glycol
(v) chloroform
(vi) pentanol
Sol: (i) Phenol (having polar – OH group) – Partially soluble.
(ii) Toluene (non-polar) – Insoluble.
(iii) Formic acid (form hydrogen bonds with water molecules) – Highly soluble.
(iv) Ethylene glycol (form hydrogen bonds with water molecules) Highly soluble.
(v) Chloroform (non-polar)- Insoluble.
(vi) Pentanol (having polar -OH) – Partially soluble.
2.26. If the density of lake water is 1·25 g mL-1, and it contains 92 g of Na+ ions per kg of water, calculate the molality of Na+ ions in the lake. (C.B.S.E. Outside Delhi 2008)
Sol:
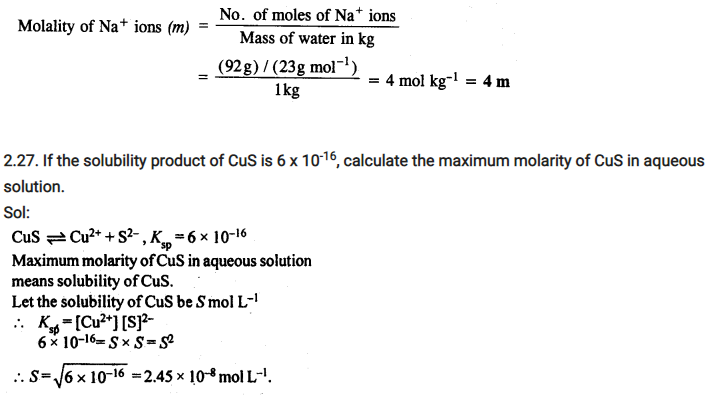


Additional information: Aspirin is the common name for acetyl salicylic acid. It is prepared by the reaction of ethanoic anhydride and salicylic acid. It is commonly used as a medicine.
Note: Mass percent is asked here, so masses are divided and multiplied by 100. When the concentration is asked in moles, then molarity is used, which is the amount of solute in gram, per liter of solution (in L).



Calculate the depression in the freezing point of water when 10 g of CH3CH2CHClCOOH is added to 250 g of water. Ka = 1.4 x 10-3, Kf = 1.86 K kg mol-1.
Molar mass of CH3CH2CHClCOOH
15 + 14 + 13 + 35.5 + 12 + 16 + 16 + 1
= 122.5 g/mol
∴ Moles of CH3CH2CHClCOOH = 10g / 122.5 g/mol
= 0.0816 mol
Therefore molality of the solution
= (0.0816 x 1000) / 250
= 0.3265 mol kg-1
Now if a is the degree of dissociation of CH3CH2CHClCOOH,

Therefore ΔTf = i Kf m v
= 1.065 v x 1.86 x 0.3265
= 0.647°
19.5 g of CH2FCOOH is dissolved in 500 g of water. The depression in the freezing point of water observed is 1.0°C. Calculate the van’t Hoff factor and dissociation constant of fluoroacetic acid.
Molecular mass of CH2FCOOH
14 + 19 + 12 + 16 + 16 + 1 = 78 g/mol
Now, Moles of CH2FCOOH = 19.5 / 78
= 0.25
Taking the volume of the solution as 500 mL, we have the concentration:
C = (0.25 / 500) X 1000
Therefore Molality = 0.50m
So now putting the value in the formula :
ΔTf = Kf x m
=1.86 x 0.50 = 0.93K
Van’t hoff factor = observed freezing point depression / calculated freezing point depression
= 1 / 0.93 = 1.0753
Let α be the degree of dissociation of CH2FCOOH


Henry’s law constant for the molality of methane in benzene at 298 Kis 4.27 x 105 mm Hg. Calculate the solubility of methane in benzene at 298 Kunder 760 mm Hg.
As we know that
p = k x c
We have given p = 760 mm, k = 4.27x 105
Putting the given values in equation
760 = 4.27x 105 x c
Or
c = 760 / 4.27x 105
c = 178 x 10-5
100 g of liquid A (molar mass 140 g mol-1) was dissolved in 1000 g of liquid B (molar mass 180 g mol-1). The vapour pressure of pure liquid B was found to be 500 torr. Calculate the vapour pressure of pure liquid A and its vapour pressure in the solution if the total vapour pressure of the solution is 475 Torr.
Number of Moles of Liquid A, nA = 100 / 140 = 0.714
Number of Moles of Liquid B, nB = 1000 / 180 = 5.556
Then Mole fraction of A = nA / nA + nB = 0.714 / 0.714 + 5.556
= 0.114
Now Mole of fraction of B = 1 – 0.114 = 0.886
Now ptotal = pA + pB
Or ptotal = p°AXA + p°BxB
OR
475 = p°A X 0.114 + 500 X 0.886
OR
p°A = 280.7 torr
Therefore vapour pressure of pure A = 280.7 torr
Vapour pressure of A in solution = 280.7 x 0.114
= 32 torr
Now
pA = p°AXA
Or
p°A = pA / XA
⇒ 32 / 0.114
= 280.7 torr
Hence, the vapour pressure of pure liquid A is 280.7 torr.

From the question, we have the following data
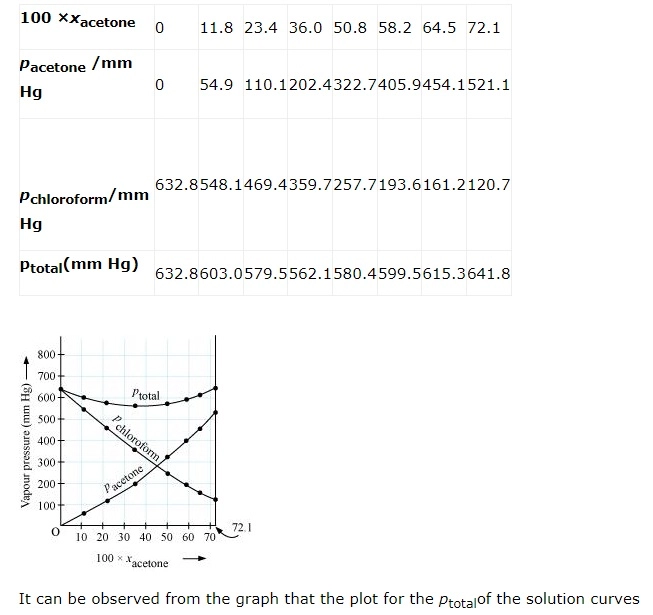
downwards. Therefore, the solution shows negative deviation from the ideal behaviour.
Question 38
Benzene and toluene form ideal solution over the entire range of composition. The vapour pressure of pure benzene and toluene at 300 K are 50.71 mm Hg and 32.06 mm Hg respectively. Calculate the mole fraction of benzene in vapour phase if 80 g of benzene is mixed with 100 g of toluene.
Molar mass of benzene(C6H6) = 6 X 12 + 6 X 1 = 78 g/mol
Molar mass of toluene = 7 x 12 + 8 x 1 = 92 g/mol
Now no of moles in 80g of benezen = 80 / 78 = 1.026 mol
No of moles in 100g of toluene = 100 / 92 = 1.087 mol
∴Mole fraction of benzene xb = 1.026 / 1.026 + 1.087 = 0.486
And Mole fraction of toluene,xt = 1 – 0.486 = 0.514
We have given that
Vapor pressure of pure benzene pb° = 50.71 mm Hg
And, vapour pressure of pure toluene, pt° = 32.06 mm Hg
Therefore partial Vapor pressure of benzene, pb = pb X xb
= 50.71 x 0.486
= 24.65 mm Hg
And partial Vapor pressure of toluene, pt = pt X xt
Pt = p°t X xt = 32.06 x 0.514
= 16.48
Total vapour pressure = 24.65 + 16.48 = 41.13 mm Hg
Mole fraction of benzene in vapour phase = 24.65 / 41.13 = 0.60

Determine the amount of CaCl2 (i = 2.47) dissolved in 2.5 litre of water such that its osmotic pressure is 0.75 atm at 27°C.
We know that
π = i n/V RT
⇒π = i w/MV iRT
⇒ w = πMV / iRT …………………..(1)
Now we have given below values:
π = 0.75 atm
V = 2.5L
i = 2.47
T = (27+273) K = 300K
Here,
R = 0.0821L atm k-1 mol-1
M = 1×40 + 2×35.5
= 111 g/mol
Now putting the value in equation 1:
w = 0.75x111x2.5 / 2.47×0.0821×300
=3.42g
Hence, the required amount of CaCl2 is 3.42 g.
