Circles Full Video || Chapter – 10 || Class 10th (For Hindi Medium)

Circle and line in a plane

For a circle and a line on a plane, there can be three possibilities.

i) they can be non-intersecting

ii) they can have a single common point: in this case, the line touches the circle.

ii) they can have two common points: in this case, the line cuts the circle.

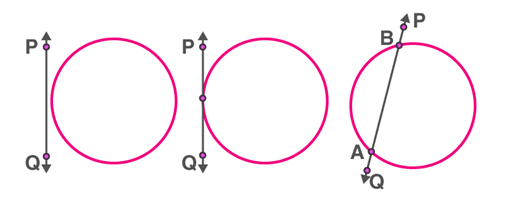
(i) Non intersecting   (ii) Touching  (iii) Intersecting

Tangent

A tangent to a circle is a line which touches the circle at exactly one point. For every point on the circle, there is a unique tangent passing through it.

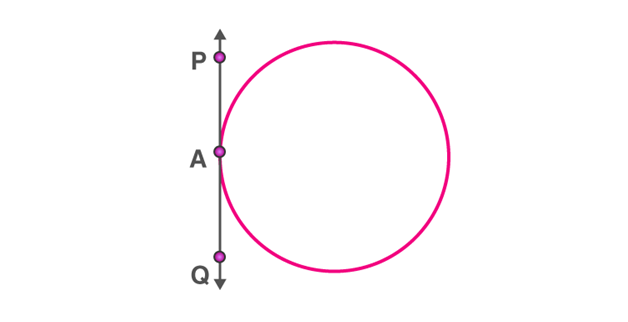
Tangent

To know more about Tangent, visit here.

Secant

A secant to a circle is a line which has two points in common with the circle. It cuts the circle at two points, forming a chord of the circle.

Secant

To know more about Secant, visit here.

Tangent as a special case of Secant

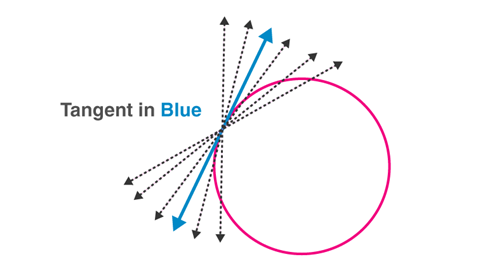
Tangent as a special case of Secant

The tangent to a circle can be seen as a special case of the secant when the two endpoints of its corresponding chord coincide.

Two parallel tangents at most for a given secant

For every given secant of a circle, there are exactly two tangents which are parallel to it and touches the circle at two diametrically opposite points.

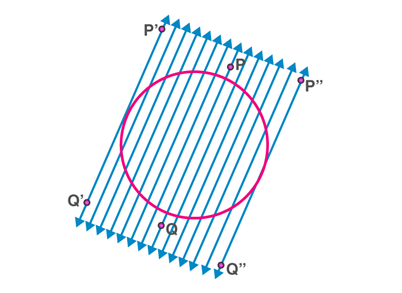
Parallel tangents

Theorems

Tangent perpendicular to the radius at the point of contact

Theorem: The theorem states that “the tangent to the circle at any point is the perpendicular to the radius of the circle that passes through the point of contact”.

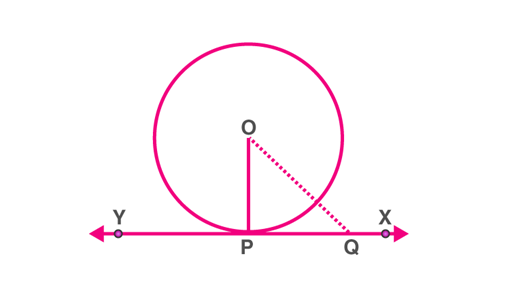
Tangent and radius

Here, O is the centre and OP⊥XY.

The number of tangents drawn from a given point

i) If the point is in an interior region of the circle, any line through that point will be a secant. So, no tangent can be drawn to a circle which passes through a point that lies inside it.

AB is a secant drawn through the point S

ii) When a point of tangency lies on the circle, there is exactly one tangent to a circle that passes through it.

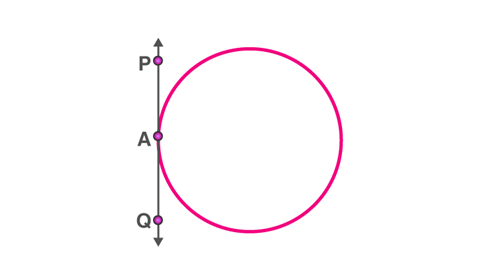
A tangent passing through a point lying on the circle

iii) When the point lies outside of the circle, there are accurately two tangents to a circle through it

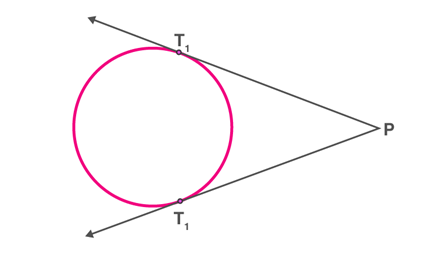
Tangents to a circle from an external point

Length of a tangent

The length of the tangent from the point (Say P) to the circle is defined as the segment of the tangent from the external point P to the point of tangency I with the circle. In this case, PI is the tangent length.

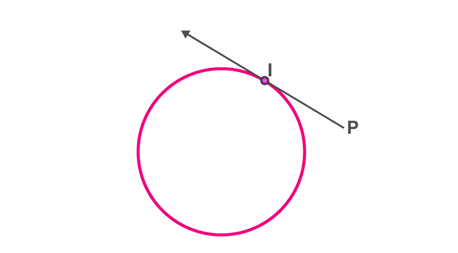
Lengths of tangents drawn from an external point

Theorem: Two tangents are of equal length when the tangent is drawn from an external point to a circle.

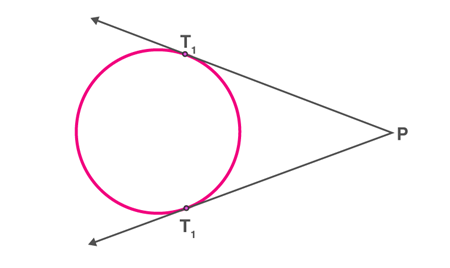
Tangents to a circle from an external point

PT1=PT2