Exercise 6.5 Page: 150
1. Sides of triangles are given below. Determine which of them are right triangles? In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Solution:
(i) Given, sides of the triangle are 7 cm, 24 cm, and 25 cm.
Squaring the lengths of the sides of the, we will get 49, 576, and 625.
49 + 576 = 625
(7)2 + (24)2 = (25)2
Therefore, the above equation satisfies, Pythagoras theorem. Hence, it is right angled triangle.
Length of Hypotenuse = 25 cm
(ii) Given, sides of the triangle are 3 cm, 8 cm, and 6 cm.
Squaring the lengths of these sides, we will get 9, 64, and 36.
Clearly, 9 + 36 ≠ 64
Or, 32 + 62 ≠ 82
Therefore, the sum of the squares of the lengths of two sides is not equal to the square of the length of the hypotenuse.
Hence, the given triangle does not satisfies Pythagoras theorem.
(iii) Given, sides of triangle’s are 50 cm, 80 cm, and 100 cm.
Squaring the lengths of these sides, we will get 2500, 6400, and 10000.
However, 2500 + 6400 ≠ 10000
Or, 502 + 802 ≠ 1002
As you can see, the sum of the squares of the lengths of two sides is not equal to the square of the length of the third side.
Therefore, the given triangle does not satisfies Pythagoras theorem.
Hence, it is not a right triangle.
(iv) Given, sides are 13 cm, 12 cm, and 5 cm.
Squaring the lengths of these sides, we will get 169, 144, and 25.
Thus, 144 +25 = 169
Or, 122 + 52 = 132
The sides of the given triangle are satisfying Pythagoras theorem.
Therefore, it is a right triangle.
Hence, length of the hypotenuse of this triangle is 13 cm.
2. PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM × MR.
Solution:
Given, ΔPQR is right angled at P is a point on QR such that PM ⊥QR
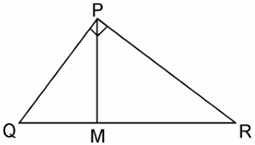
We have to prove, PM2 = QM × MR
In ΔPQM, by Pythagoras theorem
PQ2 = PM2 + QM2
Or, PM2 = PQ2 – QM2 ……………………………..(i)
In ΔPMR, by Pythagoras theorem
PR2 = PM2 + MR2
Or, PM2 = PR2 – MR2 ………………………………………..(ii)
Adding equation, (i) and (ii), we get,
2PM2 = (PQ2 + PM2) – (QM2 + MR2)
= QR2 – QM2 – MR2 [∴ QR2 = PQ2 + PR2]
= (QM + MR)2 – QM2 – MR2
= 2QM × MR
∴ PM2 = QM × MR
3. In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that
(i) AB2 = BC × BD
(ii) AC2 = BC × DC
(iii) AD2 = BD × CD

Solution:
(i) In ΔADB and ΔCAB,
∠DAB = ∠ACB (Each 90°)
∠ABD = ∠CBA (Common angles)
∴ ΔADB ~ ΔCAB [AA similarity criterion]
⇒ AB/CB = BD/AB
⇒ AB2 = CB × BD
(ii) Let ∠CAB = x
In ΔCBA,
∠CBA = 180° – 90° – x
∠CBA = 90° – x
Similarly, in ΔCAD
∠CAD = 90° – ∠CBA
= 90° –x
∠CDA = 180° – 90° – (90° – x)
∠CDA = x
In ΔCBA and ΔCAD, we have
∠CBA = ∠CAD
∠CAB = ∠CDA
∠ACB = ∠DCA (Each 90°)
∴ ΔCBA ~ ΔCAD [AAA similarity criterion]
⇒ AC/DC = BC/AC
⇒ AC2 = DC × BC
(iii) In ΔDCA and ΔDAB,
∠DCA = ∠DAB (Each 90°)
∠CDA = ∠ADB (common angles)
∴ ΔDCA ~ ΔDAB [AA similarity criterion]
⇒ DC/DA = DA/DA
⇒ AD2 = BD × CD
4. ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2 .
Solution:
Given, ΔABC is an isosceles triangle right angled at C.
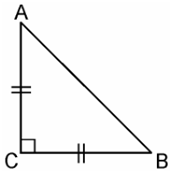
In ΔACB, ∠C = 90°
AC = BC (By isosceles triangle property)
AB2 = AC2 + BC2 [By Pythagoras theorem]
= AC2 + AC2 [Since, AC = BC]
AB2 = 2AC2
5. ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
Solution:
Given, ΔABC is an isosceles triangle having AC = BC and AB2 = 2AC2
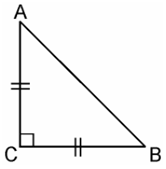
In ΔACB,
AC = BC
AB2 = 2AC2
AB2 = AC2 + AC2
= AC2 + BC2 [Since, AC = BC]
Hence, by Pythagoras theorem ΔABC is right angle triangle.
6. ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution:
Given, ABC is an equilateral triangle of side 2a.
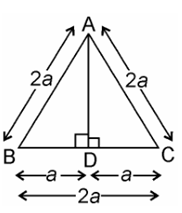
Draw, AD ⊥ BC
In ΔADB and ΔADC,
AB = AC
AD = AD
∠ADB = ∠ADC [Both are 90°]
Therefore, ΔADB ≅ ΔADC by RHS congruence.
Hence, BD = DC [by CPCT]
In right angled ΔADB,
AB2 = AD2 + BD2
(2a)2 = AD2 + a2
⇒ AD2 = 4a2 – a2
⇒ AD2 = 3a2
⇒ AD = √3a
7. Prove that the sum of the squares of the sides of rhombus is equal to the sum of the squares of its diagonals.
Solution:
Given,ABCD is a rhombus whose diagonals AC and BD intersect at O.
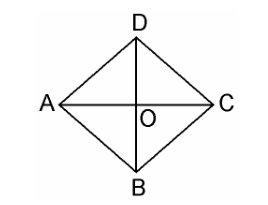
We have to prove, as per the question,
AB2 + BC2 + CD2 + AD2 = AC2 + BD2
Since, the diagonals of a rhombus bisect each other at right angles.
Therefore, AO = CO and BO = DO
In ΔAOB,
∠AOB = 90°
AB2 = AO2 + BO2 …………………….. (i) [By Pythagoras theorem]
Similarly,
AD2 = AO2 + DO2 …………………….. (ii)
DC2 = DO2 + CO2 …………………….. (iii)
BC2 = CO2 + BO2 …………………….. (iv)
Adding equations (i) + (ii) + (iii) + (iv), we get,
AB2 + AD2 +DC2 +BC2 = 2(AO2 + BO2 + DO2 + CO2)
= 4AO2 + 4BO2 [Since, AO = CO and BO =DO]
= (2AO)2 + (2BO)2 = AC2 + BD2
AB2 + AD2 +DC2 +BC2 = AC2 + BD2
Hence, proved.
8. In Fig. 6.54, O is a point in the interior of a triangle.

ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2 ,
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2.
Solution:
Given, in ΔABC, O is a point in the interior of a triangle.
And OD ⊥ BC, OE ⊥ AC and OF ⊥ AB.
Join OA, OB and OC
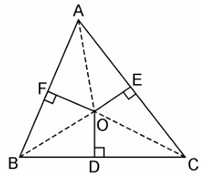
(i) By Pythagoras theorem in ΔAOF, we have
OA2 = OF2 + AF2
Similarly, in ΔBOD
OB2 = OD2 + BD2
Similarly, in ΔCOE
OC2 = OE2 + EC2
Adding these equations,
OA2 + OB2 + OC2 = OF2 + AF2 + OD2 + BD2 + OE2 + EC2
OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2.
(ii) AF2 + BD2 + EC2 = (OA2 – OE2) + (OC2 – OD2) + (OB2 – OF2)
∴ AF2 + BD2 + CE2 = AE2 + CD2 + BF2.
9. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Solution:
Given, a ladder 10 m long reaches a window 8 m above the ground.

Let BA be the wall and AC be the ladder,
Therefore, by Pythagoras theorem,
AC2 =AB2 + BC2
102 = 82 + BC2
BC2 = 100 – 64
BC2 = 36
BC= 6m
Therefore, the distance of the foot of the ladder from the base of the wall is 6 m.
10. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution:
Given, a guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end.
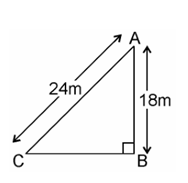
Let AB be the pole and AC be the wire.
By Pythagoras theorem,
AC2 =AB2 + BC2
242 = 182 + BC2
BC2 = 576 – 324
BC2 = 252
BC= 6√7m
Therefore, the distance from the base is 6√7m.
11. An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after
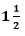
hours?
Solution:
Given,
Speed of first aeroplane = 1000 km/hr Distance covered by first aeroplane flying due north in

hours (OA) = 100 × 3/2 km = 1500 km
Speed of second aeroplane = 1200 km/hr Distance covered by second aeroplane flying due west in
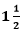
hours (OB) = 1200 × 3/2 km = 1800 km
In right angle ΔAOB, by Pythagoras Theorem,
AB2 =AO2 + OB2
⇒ AB2 =(1500)2 + (1800)2
⇒ AB = √(2250000 + 3240000)
= √5490000
⇒ AB = 300√61 km
Hence, the distance between two aeroplanes will be 300√61 km.
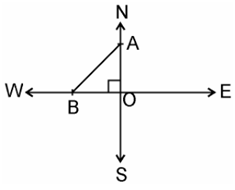
12. Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution:
Given, Two poles of heights 6 m and 11 m stand on a plane ground.
And distance between the feet of the poles is 12 m.
Let AB and CD be the poles of height 6m and 11m.
Therefore, CP = 11 – 6 = 5m
From the figure, it can be observed that AP = 12m
By Pythagoras theorem for ΔAPC, we get,
AP2 =PC2 + AC2
(12m)2 + (5m)2 = (AC)2
AC2 = (144+25) m2 = 169 m2
AC = 13m
Therefore, the distance between their tops is 13 m.
13. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2.
Solution:
Given, D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C.

By Pythagoras theorem in ΔACE, we get
AC2 +CE2 = AE2 ………………………………………….(i)
In ΔBCD, by Pythagoras theorem, we get
BC2 +CD2 = BD2 ………………………………..(ii)
From equations (i) and (ii), we get,
AC2 +CE2 + BC2 +CD2 = AE2 + BD2 …………..(iii)
In ΔCDE, by Pythagoras theorem, we get
DE2 =CD2 + CE2
In ΔABC, by Pythagoras theorem, we get
AB2 =AC2 + CB2
Putting the above two values in equation (iii), we get
DE2 + AB2 = AE2 + BD2.
14. The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD (see Figure). Prove that 2AB2 = 2AC2 + BC2.
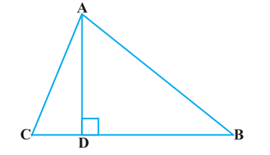
Solution:
Given, the perpendicular from A on side BC of a Δ ABC intersects BC at D such that;
DB = 3CD.
In Δ ABC,
AD ⊥BC and BD = 3CD
In right angle triangle, ADB and ADC, by Pythagoras theorem,
AB2 =AD2 + BD2 ……………………….(i)
AC2 =AD2 + DC2 ……………………………..(ii)
Subtracting equation (ii) from equation (i), we get
AB2 – AC2 = BD2 – DC2
= 9CD2 – CD2 [Since, BD = 3CD]
= 8CD2
= 8(BC/4)2 [Since, BC = DB + CD = 3CD + CD = 4CD]
Therefore, AB2 – AC2 = BC2/2
⇒ 2(AB2 – AC2) = BC2
⇒ 2AB2 – 2AC2 = BC2
∴ 2AB2 = 2AC2 + BC2.
15. In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3BC. Prove that 9AD2 = 7AB2.
Solution:
Given, ABC is an equilateral triangle.
And D is a point on side BC such that BD = 1/3BC
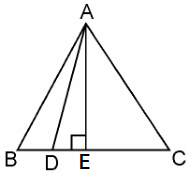
Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC.
∴ BE = EC = BC/2 = a/2
And, AE = a√3/2
Given, BD = 1/3BC
∴ BD = a/3
DE = BE – BD = a/2 – a/3 = a/6 In ΔADE, by Pythagoras theorem,
AD2 = AE2 + DE2
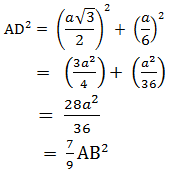
⇒ 9 AD2 = 7 AB2
16. In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution:
Given, an equilateral triangle say ABC,
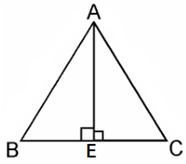
Let the sides of the equilateral triangle be of length a, and AE be the altitude of ΔABC.
∴ BE = EC = BC/2 = a/2
In ΔABE, by Pythagoras Theorem, we get
AB2 = AE2 + BE2
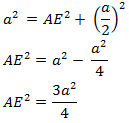
4AE2 = 3a2
⇒ 4 × (Square of altitude) = 3 × (Square of one side)
Hence, proved.
17. Tick the correct answer and justify: In ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm.
The angle B is:
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Solution:
Given, in ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm.
We can observe that,
AB2 = 108
AC2 = 144
And, BC2 = 36
AB2 + BC2 = AC2
The given triangle, ΔABC, is satisfying Pythagoras theorem.
Therefore, the triangle is a right triangle, right-angled at B.
∴ ∠B = 90°
Hence, the correct answer is (C).