Introduction to Quadratic Equations
Quadratic Polynomial
A polynomial of the form ax2+bx+c, where a,b and c are real numbers and a≠0 is called a quadratic polynomial.
Quadratic Equation
When we equate a quadratic polynomial to a constant, we get a quadratic equation.
Any equation of the form p(x)=c, where p(x) is a polynomial of degree 2 and c is a constant, is a quadratic equation.
The standard form of a Quadratic Equation
The standard form of a quadratic equation is ax2+bx+c=0, where a,b and c are real numbers and a≠0.
‘a’ is the coefficient of x2. It is called the quadratic coefficient. ‘b’ is the coefficient of x. It is called the linear coefficient. ‘c’ is the constant term.
Solving QE by Factorisation
Roots of a Quadratic equation
The values of x for which a quadratic equation is satisfied are called the roots of the quadratic equation.
If α is a root of the quadratic equation ax2+bx+c=0, then aα2+bα+c=0.
A quadratic equation can have two distinct real roots, two equal roots or real roots may not exist.
Graphically, the roots of a quadratic equation are the points where the graph of the quadratic polynomial cuts the x-axis.
Consider the graph of a quadratic equation x2−4=0:
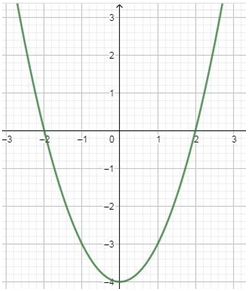
Graph of a Quadratic Equation
In the above figure, -2 and 2 are the roots of the quadratic equation x2−4=0
Note:
- If the graph of the quadratic polynomial cuts the x-axis at two distinct points, then it has real and distinct roots.
- If the graph of the quadratic polynomial touches the x-axis, then it has real and equal roots.
- If the graph of the quadratic polynomial does not cut or touch the x-axis then it does not have any real roots.
Solving a Quadratic Equation by Factorization method
Consider a quadratic equation 2×2−5x+3=0
⇒2×2−2x−3x+3=0
This step is splitting the middle term
We split the middle term by finding two numbers (-2 and -3) such that their sum is equal to the coefficient of x and their product is equal to the product of the coefficient of x2 and the constant.
(-2) + (-3) = (-5)
And (-2) × (-3) = 6
2×2−2x−3x+3=0
2x(x−1)−3(x−1)=0
(x−1)(2x−3)=0
In this step, we have expressed the quadratic polynomial as a product of its factors.
Thus, x = 1 and x =3/2 are the roots of the given quadratic equation.
This method of solving a quadratic equation is called the factorisation method.
Solving QE by Completing the Square
Solving a Quadratic Equation by Completion of squares method
In the method of completing the squares, the quadratic equation is expressed in the form (x±k)2=p2.
Consider the quadratic equation 2×2−8x=10
(i) Express the quadratic equation in standard form.
2×2−8x−10=0
(ii) Divide the equation by the coefficient of x2 to make the coefficient of x2 equal to 1.
x2−4x−5=0
(iii) Add the square of half of the coefficient of x to both sides of the equation to get an expression of the form x2±2kx+k2.
(x2−4x+4)−5=0+4
(iv) Isolate the above expression, (x±k)2 on the LHS to obtain an equation of the form (x±k)2=p2
(x−2)2=9
(v) Take the positive and negative square roots.
x−2=±3
x=−1 or x=5
Solving QE Using Quadratic Formula
Quadratic Formula
Quadratic Formula is used to directly obtain the roots of a quadratic equation from the standard form of the equation.
For the quadratic equation ax2+bx+c=0,
x= [-b± √(b2-4ac)]/2a
By substituting the values of a,b and c, we can directly get the roots of the equation.
Discriminant
For a quadratic equation of the form ax2+bx+c=0, the expression b2−4ac is called the discriminant, (denoted by D), of the quadratic equation.
The discriminant determines the nature of roots of the quadratic equation based on the coefficients of the quadratic equation.
Solving using Quadratic Formula when D>0
Solve 2×2−7x+3=0 using the quadratic formula.
(i) Identify the coefficients of the quadratic equation. a = 2,b = -7,c = 3
(ii) Calculate the discriminant, b2−4ac
D=(−7)2−4×2×3= 49-24 = 25
D> 0, therefore, the roots are distinct.
(iii) Substitute the coefficients in the quadratic formula to find the roots
x= [-(-7)± √((-7)2-4(2)(3))]/2(2)
x=(7 ±5)/4
x=3 and x= 1/2 are the roots.
Nature of Roots
Based on the value of the discriminant, D=b2−4ac, the roots of a quadratic equation can be of three types.
Case 1: If D>0, the equation has two distinct real roots.
Case 2: If D=0, the equation has two equal real roots.
Case 3: If D<0, the equation has no real roots.
Graphical Representation of a Quadratic Equation
The graph of a quadratic polynomial is a parabola. The roots of a quadratic equation are the points where the parabola cuts the x-axis i.e. the points where the value of the quadratic polynomial is zero.
Now, the graph of x2+5x+6=0 is:
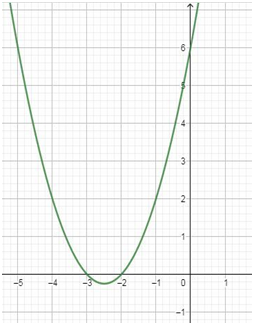
In the above figure, -2 and -3 are the roots of the quadratic equation
x2+5x+6=0.
For a quadratic polynomial ax2+bx+c,
If a>0, the parabola opens upwards.
If a<0, the parabola opens downwards.
If a = 0, the polynomial will become a first-degree polynomial and its graph is linear.
The discriminant, D=b2−4ac

Nature of graph for different values of D.
If D>0, the parabola cuts the x-axis at exactly two distinct points. The roots are distinct. This case is shown in the above figure in a, where the quadratic polynomial cuts the x-axis at two distinct points.
If D=0, the parabola just touches the x-axis at one point and the rest of the parabola lies above or below the x-axis. In this case, the roots are equal.
This case is shown in the above figure in b, where the quadratic polynomial touches the x-axis at only one point.
If D<0, the parabola lies entirely above or below the x-axis and there is no point of contact with the x-axis. In this case, there are no real roots.
This case is shown in the above figure in c, where the quadratic polynomial neither cuts nor touches the x-axis.
Formation of a quadratic equation from its roots
To find out the standard form of a quadratic equation when the roots are given:
Let α and β be the roots of the quadratic equation ax2+bx+c=0. Then,
(x−α)(x−β)=0
On expanding, we get,
x2−(α+β)x+αβ=0, which is the standard form of the quadratic equation. Here, a=1,b=−(α+β) and c=αβ.
Sum and Product of Roots of a Quadratic equation
Let α and β be the roots of the quadratic equation ax2+bx+c=0. Then,
Sum of roots =α+β=-b/a
Product of roots =αβ= c/a