Coordinate Geometry|| Chapter – 7|| Class 10th (For Hindi medium)

Introduction to Coordinate Geometry

Basics of Coordinate Geometry

Points on a Cartesian Plane

A pair of numbers locate points on a plane called the coordinates.  The distance of a point from the y-axis is known as abscissa or x-coordinate. The distance of a point from the x-axis is called ordinates or y-coordinate.

Representation of (x, y) on the cartesian plane

Distance Formula

Distance between Two Points on the Same Coordinate Axes

The distance between two points which are on the same axis (x-axis or y-axis), is given by the difference between their ordinates if they are on the y-axis, else by the difference between their abscissa if they are on the x-axis.

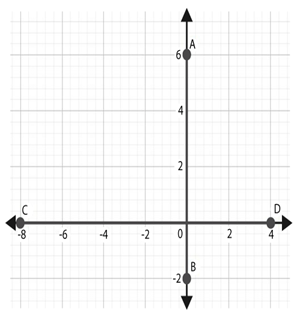
Distance AB = 6 – (-2) = 8 units

Distance CD = 4 – (-8) = 12 units

Distance between Two Points Using Pythagoras Theorem

Finding distance between 2 points using
Pythagoras Theorem

Let P(x1, y1) and Q(x2, y2) be any two points on the cartesian plane.
Draw lines parallel to the axes through P and Q to meet at T.

ΔPTQ  is right-angled at T.

By Pythagoras Theorem,
PQ2 = PT2 + QT2

= (x2 – x1)² + (y2 – y1)²

PQ = √[x2 – x1)² + (y2 – y1)²]

Distance Formula

Distance between any two points (x1, y1) and (x2, y2) is given by
d = √[x2 – x1)²+(y2 – y1)²]
Where d is the distance between the points (x1,y1) and (x2,y2).

Section Formula

If the point P(x, y) divides the line segment joining A(x1, y1) and B(x2, y2) internally in the ratio m:n, then, the coordinates of P are given by the section formula as:

P(x, y)=(mx2+nx1m+n,my2+ny1m+n)

Finding ratio given the points

To find the ratio in which a given point P(x, y) divides the line segment joining A(x1, y1) and B(x2, y2),

• Assume that the ratio is k : 1
• Substitute the ratio in the section formula for any of the coordinates to get the value of k.

x=kx2+x1k+1

When x1, x2 and x are known, k can be calculated. The same can be calculated from the y- coordinate also.

MidPoint

The midpoint of any line segment divides it in the ratio 1 : 1.
The coordinates of the midpoint(P) of line segment joining A(x1, y1) and B(x2, y2) is given by
p(x, y)=(x1+x22,y1+y22)

Points of Trisection

To find the points of trisection P and Q which divides the line segment joining
A(x1, y1) and B(x2, y2) into three equal parts:

i) AP : PB = 1 : 2

P=(x2+2×13,y2+2y13)

ii) AQ : QB = 2 : 1
Q=(2×2+x13,2y2+y13)

Centroid of a triangle

If A(x1, y1),B(x2, y2) and C(x3, y3) are the vertices of a ΔABC, then the coordinates of its centroid(P) is given by
p(x, y)=(x1+x2+x33,y1+y2+y33)

Area from Coordinates

Area of a triangle given its vertices

If A(x1, y1),B(x2, y2) and C(x3, y3) are the vertices of a Δ ABC, then its area is given by

A = 1/2[x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)]
Where A is the area of the Δ ABC.

Collinearity Condition

If three points A, B and C are collinear and B lies between A and C, then,

• AB + BC = AC.  AB, BC, and AC can be calculated using the distance formula.
• The ratio in which B divides AC, calculated using section formula for both the x and y coordinates separately will be equal.
• Area of a triangle formed by three collinear points is zero.