Construction Full Video || Chapter – 11 || Class 10th (For Hindi Medium)

Dividing a Line Segment

Bisecting a Line Segment

Step 1: With a radius of more than half the length of the line-segment, draw arcs centred at either end of the line segment so that they intersect on either side of the line segment.

Step 2: Join the points of intersection. The line segment is bisected by the line segment joining the points of intersection.

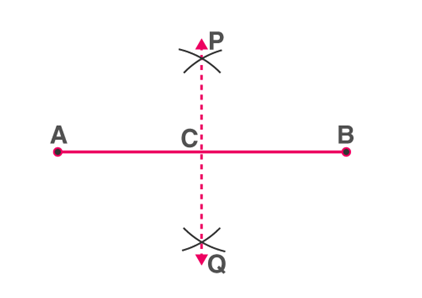
PQ is the perpendicular bisector of AB

2) Given a line segment AB, divide it in the ratio m:n, where both m and n are positive integers.

Suppose we want to divide AB in the ratio 3:2 (m=3, n=2)

Step 1: Draw any ray AX, making an acute angle with line segment AB.

Step 2: Locate 5 (= m + n) points A1,A2,A3,A4andA5 on AX such that AA1=A1A2=A2A3=A3A4=A4A5

Step 3: Join BA5.(A(m+n)=A5)

Step 4: Through the point A3(m=3), draw a line parallel to BA5 (by making an angle equal to ∠AA5B) at A3 intersecting AB at the point C.

Then, AC : CB = 3 : 2.

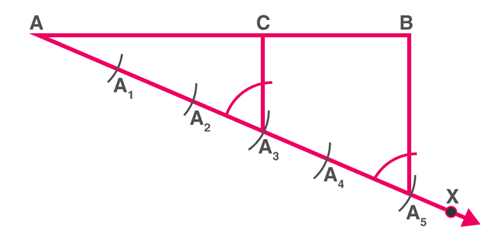
Division of a line segment

To know more about Dividing a Line Segment, visit here.

Constructing Similar Triangles

Constructing a Similar Triangle with a scale factor

Suppose we want to construct a triangle whose sides are 3/4 times the corresponding sides of a given triangle

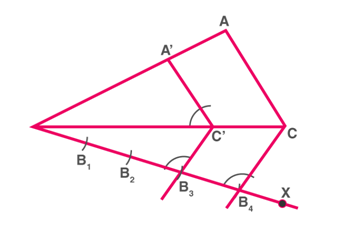
Step 1: Draw any ray BX making an acute angle with side BC  (on the side opposite to the vertex A).

Step 2: Mark 4 consecutive distances(since the denominator of the required ratio is 4) on BX  as shown.

Step 3: Join B4C as shown in the figure.

Step 4: Draw a line through B3 parallel to B4C to intersect BC at C’.

Step 5: Draw a line through C’ parallel to AC to intersect AB at  A’. ΔA′BC′ is the required triangle.

The same procedure can be followed when the scale factor > 1.

To know more about Constructing Similar Triangles, visit here.

Drawing Tangents to a Circle

Tangents: Definition

A tangent to a circle is a line which touches the circle at exactly one point.

For every point on the circle, there is a unique tangent passing through it.

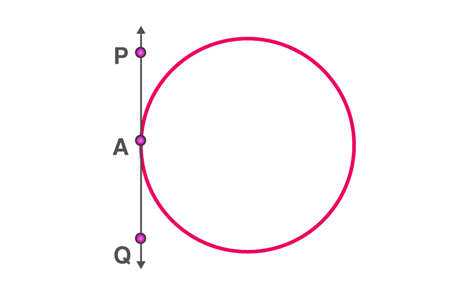
PQ is the tangent, touching the circle at A

To know more about Drawing Tangents to a Circle, visit here.

Number of Tangents to a circle from a given point

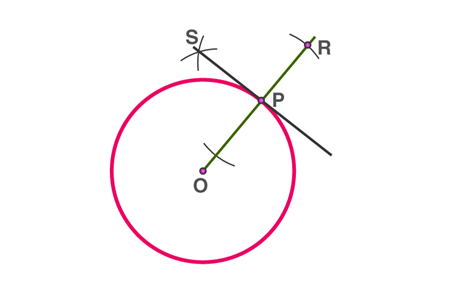
i) If the point in an interior region of the circle, any line through that point will be a secant. So, in this case, there is no tangent to the circle.

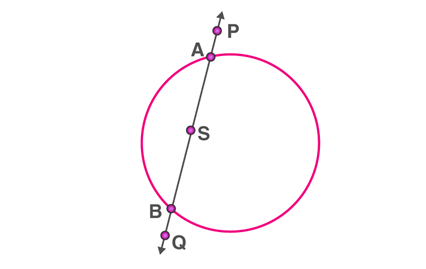
AB is a secant drawn through the point S

ii) When the point lies on the circle, there is accurately only one tangent to a circle.

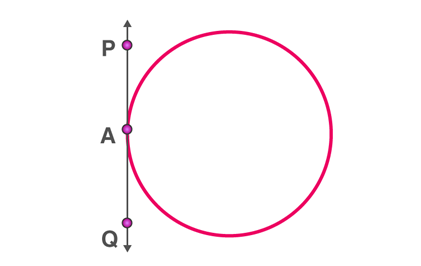
PQ is the tangent touching the circle at A

iii) When the point lies outside of the circle, there are exactly two tangents to a circle.

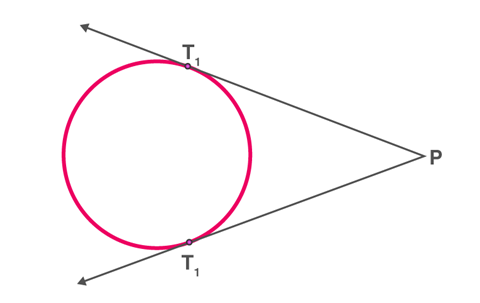
PT1 and PT2 are tangents touching the circle at T1 and T2

Drawing tangents to a circle from a point outside the circle

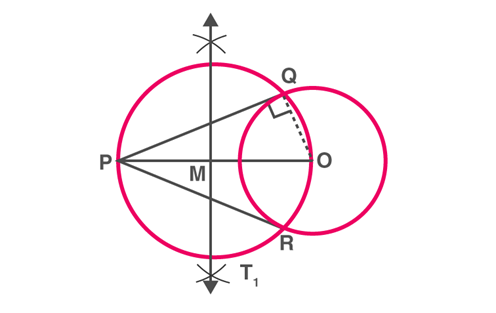
To construct the tangents to a circle from a point outside it.

Consider a circle with centre O and let P be the exterior point from which the tangents to be drawn.

Step 1: Join the PO and bisect it. Let M be the midpoint of PO.

Step 2: Taking M as the centre and MO(or MP) as radius, draw a circle. Let it intersect the given circle at the points Q and R.

Step 3: Join PQ and PR

Step 3:PQ and PR are the required tangents to the circle.

Drawing Tangents to a circle from a point on the circle

To draw a tangent to a circle through a point on it.

Step 1: Draw the radius of the circle through the required point.
Step 2: Draw a line perpendicular to the radius through this point. This will be tangent to the circle.