Exercise: 13.5 (Optional) (Page No: 258)

1. A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm³.

Solution:

Given that,

Diameter of cylinder = 10 cm

So, radius of the cylinder (r) = 10/2 cm = 5 cm

∴ Length of wire in completely one round = 2πr = 3.14×5 cm = 31.4 cm

It is given that diameter of wire = 3 mm = 3/10 cm

∴ The thickness of cylinder covered in one round = 3/10 m

Hence, the number of turns (rounds) of the wire to cover 12 cm will be-

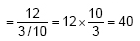
Now, the length of wire required to cover the whole surface = length of wire required to complete 40 rounds

40 x 31.4 cm = 1256 cm

Radius of the wire = 0.3/2 = 0.15 cm

Volume of wire = Area of cross-section of wire × Length of wire

= π(0.15)2×1257.14

= 88.898 cm³

We know,

Mass = Volume × Density

= 88.898×8.88

= 789.41 gm

2. A right triangle whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate)

Solution:

Draw the diagram as follows:

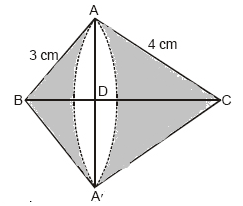
Let us consider the ABA

Here,

AS = 3 cm, AC = 4 cm

So, Hypotenuse BC = 5 cm

We have got 2 cones on the same base AA’ where the radius = DA or DA’

Now, AD/CA = AB/CB

By putting the value of CA, AB and CB we get,

AD = 2/5 cm

We also know,

DB/AB = AB/CB

So, DB = 9/5 cm

As, CD = BC-DB,

CD = 16/5 cm

Now, volume of double cone will be

Solving this we get,

V = 30.14 cm³

The surface area of the double cone will be

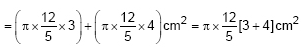
= 52.75 cm²

3. A cistern, internally measuring 150 cm × 120 cm × 100 cm, has 129600 cm³ of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each being 22.5 cm × 7.5 cm × 6.5 cm?

Solution:

Given that the dimension of the cistern = 150 × 120 × 110

So, volume = 1980000 cm³

Volume to be filled in cistern = 1980000 – 129600

= 1850400 cm³

Now, let the number of bricks placed be “n”

So, volume of n bricks will be = n×22.5×7.5×6.5

Now as each brick absorbs one-seventeenth of its volume, the volume will be

= n/(17)×(22.5×7.5×6.5)

For the condition given in the question,

The volume of n bricks has to be equal to volume absorbed by n bricks + Volume to be filled in cistern

Or, n×22.5×7.5×6.5 = 1850400+n/(17)×(22.5×7.5×6.5)

Solving this we get,

n = 1792.41

4. In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 97280 km², show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.

Solution:

From the question, it is clear that

Total volume of 3 rivers = 3×[(Surface area of a river)×Depth]

Given,

Surface area of a river = [1072×(75/1000)] km

And,

Depth = (3/1000) km

Now, volume of 3 rivers = 3×[1072×(75/1000)]×(3/1000)

= 0.72 km³

Now, volume of rainfall = total surface area × total height of rain

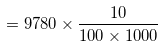
= 9.7 km³

For the total rainfall was approximately equivalent to the addition to the normal water of three rivers, the volume of rainfall has to be equal to volume of 3 rivers.

But, 9.7 km³ ≠ 0.72 km³

So, the question statement is false.

5. An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see Fig.).

Solution:

Given,

Diameter of upper circular end of frustum part = 18 cm

So, radius (r₁) = 9 cm

Now, the radius of the lower circular end of frustum (r₂) will be equal to the radius of the circular end of the cylinder

So, r₂ = 8/2 = 4 cm

Now, height (h₁) of the frustum section = 22 – 10 = 12 cm

And,

Height (h₂) of cylindrical section = 10 cm (given)

Now, the slant height will be-

Or, l = 13 cm

Area of tin sheet required = CSA of frustum part + CSA of cylindrical part

= π(r₁+r₂)l+2πr₂h₂

Solving this we get,

Area of tin sheet required = 782×(4/7) cm²

6. Derive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.

Solution:

Consider the diagram

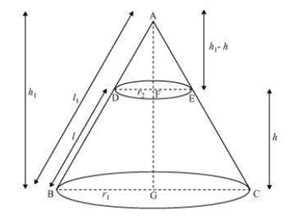
Let ABC be a cone. From the cone the frustum DECB is cut by a plane parallel to its base. Here, r₁ and r₂ are the radii of the frustum ends of the cone and h be the frustum height.

Now, consider the ΔABG and ΔADF,

Here, DF||BG

So, ΔABG ~ ΔADF

Now, by rearranging we get,

The total surface area of frustum will be equal to the total CSA of frustum + the area of upper circular end + area of the lower circular end

= π(r₁+r₂)l+πr₂²+πr₁²

∴ Surface area of frustum = π[r₁+r₂)l+r₁²+r₂²]

7. Derive the formula for the volume of the frustum of a cone.

Solution:

Consider the same diagram as the previous question.

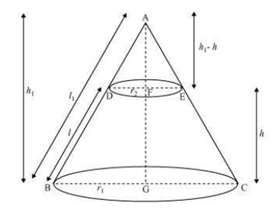
Now, approach the question in the same way as the previous one and prove that

ΔABG ~ ΔADF

Again,

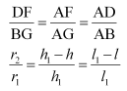
Now, rearrange them in terms of h and h₁

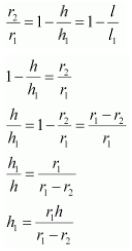
The total volume of frustum of the cone will be = Volume of cone ABC – Volume of cone ADE

= (⅓)πr₁²h₁ -(⅓)πr₂²(h₁ – h)

= (π/3)[r₁²h₁-r₂²(h₁ – h)]

Now, solving this we get,

∴ Volume of frustum of the cone = (⅓)πh(r₁²+r₂²+r₁r₂)