Introduction of Areas Related to Circles

Area of a Circle

Area of a circle is πr2, where π=22/7 or ≈3.14 (can be used interchangeably for problem-solving purposes)and r is the radius of the circle.
π is the ratio of the circumference of a circle to its diameter.

To know more about Area of a Circle, visit here.

Circumference of a Circle

The perimeter of a circle is the distance covered by going around its boundary once. The perimeter of a circle has a special name: Circumference, which is π times the diameter which is given by the formula 2πr

To know more about Circumference of a Circle, visit here.

Segment of a Circle

A circular segment  is a region of a circle which is “cut off” from the rest of the circle by a secant or a chord.

To know more about Segment of a Circle, visit here.

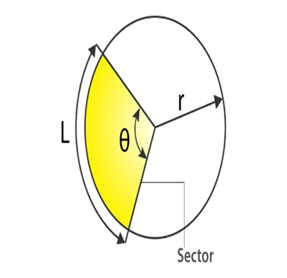
Sector of a Circle

A circle sector/ sector of a circle is defined as the region of a circle enclosed by an arc and two radii. The smaller area is called the minor sector and the larger area is called the major sector.

To know more about Sector of a Circle, visit here.

Angle of a Sector

The angle of a sector is that angle which is enclosed between the two radii of the sector.

Length of an arc of a sector

The length of the arc of a sector can be found by using the expression for the circumference of a circle and the angle of the sector, using the following formula:

L= (θ/360°)×2πr

Where θ is the angle of sector and r is the radius of the circle.

Area of a Sector of a Circle

Area of a sector is given by

(θ/360°)×πr2

where ∠θ is the angle of this sector(minor sector in the following case) and r is its radius

Area of a sector

To know more about Sector of a Circle, visit here.

Area of a Triangle

The Area of a triangle is,
Area=(1/2)×base×height
If the triangle is an equilateral then
Area=(√3/4)×a2  where “a” is the side length of the triangle.

To know more about Area of a Triangle, visit here.

Area of a Segment of a Circle

Area of segment APB (highlighted in yellow)
= (Area of sector OAPB) – (Area of triangle AOB)

=[(∅/360°)×πr2] – [(1/2)×AB×OM]

[To find the area of triangle AOB, use trigonometric ratios to find OM (height) and AB (base)]

Also, Area of segment APB can be calculated directly if the angle of the sector is known using the following formula.

 =[(θ/360°)×πr2] – [r2×sin θ/2 × cosθ/2]

Where θ is the angle of the sector and r is the radius of the circle

Visualizations

Areas of different plane figures

–    Area of a square (side l) =l2
–    Area of a rectangle =l×b, where l and b are the length and breadth of the rectangle
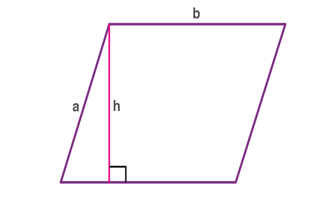
–    Area of a parallelogram =b×h, where “b” is the base and “h” is the perpendicular height.

parallelogram

Area of a trapezium =[(a+b)×h]/2,

where

a & b are the length of the parallel sides

h is the trapezium height

Area of a rhombus =pq/2, where p & q are the diagonals.

To know more about Areas of different plane figures, visit here.

Areas of Combination of Plane figures

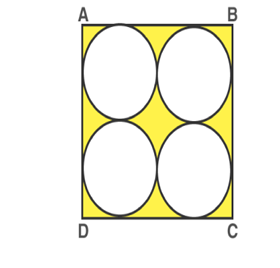
For example: Find the area of the shaded part in the following figure: Given the ABCD is a square of side 28 cm and has four equal circles enclosed within.

Area of the shaded region

Looking at the figure we can visualize that the required shaded area = A(square ABCD) − 4 ×A(Circle).

Also, the diameter of each circle is 14 cm.
=(l2)−4×(πr2)
=(282)−[4×(π×49)]
=784−[4×22/7×49]
=784−616
=168cm2