Exercise 14.4 Page: 293
1. The following distribution gives the daily income of 50 workers if a factory. Convert the distribution above to a less than type cumulative frequency distribution and draw its ogive.
| Daily income in Rupees | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Solution
Convert the given distribution table to a less than type cumulative frequency distribution, and we get
| Daily income | Frequency | Cumulative Frequency |
| Less than 120 | 12 | 12 |
| Less than 140 | 14 | 26 |
| Less than 160 | 8 | 34 |
| Less than 180 | 6 | 40 |
| Less than 200 | 10 | 50 |
From the table plot the points corresponding to the ordered pairs such as (120, 12), (140, 26), (160, 34), (180, 40) and (200, 50) on graph paper and the plotted points are joined to get a smooth curve and the obtained curve is known as less than type ogive curve
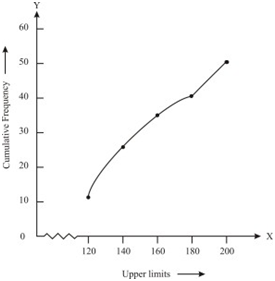
2.During the medical check-up of 35 students of a class, their weights were recorded as follows:
| Weight in kg | Number of students |
| Less than 38 | 0 |
| Less than 40 | 3 |
| Less than 42 | 5 |
| Less than 44 | 9 |
| Less than 46 | 14 |
| Less than 48 | 28 |
| Less than 50 | 32 |
| Less than 52 | 35 |
Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verify the result by using the formula.
Solution:
From the given data, to represent the table in the form of graph, choose the upper limits of the class intervals are in x-axis and frequencies on y-axis by choosing the convenient scale. Now plot the points corresponding to the ordered pairs given by (38, 0), (40, 3), (42, 5), (44, 9),(46, 14), (48, 28), (50, 32) and (52, 35) on a graph paper an join them to get a smooth curve. The curve obtained is known as less than type ogive.

Locate the point 17.5 on the y-axis and draw a line parallel to the x-axis cutting the curve at a point. From the point, draw a perpendicular line to the x-axis. The intersection point perpendicular to x-axis is the median of the given data. Now, to find the mode by making a table.
| Class interval | Number of students(Frequency) | Cumulative Frequency |
| Less than 38 | 0 | 0 |
| Less than 40 | 3-0=3 | 3 |
| Less than 42 | 5-3=2 | 8 |
| Less than 44 | 9-5=4 | 9 |
| Less than 46 | 14-9=5 | 14 |
| Less than 48 | 28-14=14 | 28 |
| Less than 50 | 32-28=4 | 32 |
| Less than 52 | 35-22=3 | 35 |
The class 46 – 48 has the maximum frequency, therefore, this is modal class
Here, l = 46, h = 2, f1= 14, f0= 5 and f2 = 4
The mode formula is given as:
Now, Mode =
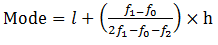
= 46 + 0.95 = 46.95
Thus, mode is verified.
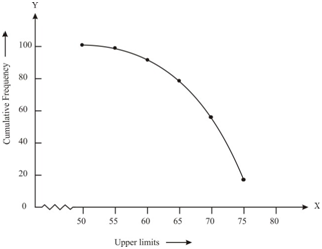
3. The following tables gives production yield per hectare of wheat of 100 farms of a village.
| Production Yield | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 | 75-80 |
| Number of farms | 2 | 8 | 12 | 24 | 38 | 16 |
Change the distribution to a more than type distribution and draw its ogive.
Solution:
Converting the given distribution to a more than type distribution, we get
| Production Yield (kg/ha) | Number of farms |
| More than or equal to 50 | 100 |
| More than or equal to 55 | 100-2 = 98 |
| More than or equal to 60 | 98-8= 90 |
| More than or equal to 65 | 90-12=78 |
| More than or equal to 70 | 78-24=54 |
| More than or equal to 75 | 54-38 =16 |
From the table obtained draw the ogive by plotting the corresponding points where the upper limits in x-axis and the frequencies obtained in the y-axis are (50, 100), (55, 98), (60, 90), (65, 78), (70, 54) and (75, 16) on
this graph paper. The graph obtained is known as more than type ogive curve.