Access Answers of Maths NCERT Chapter 11 – Constructions
Exercise 11.1 Page: 220
In each of the following, give the justification of the construction also:
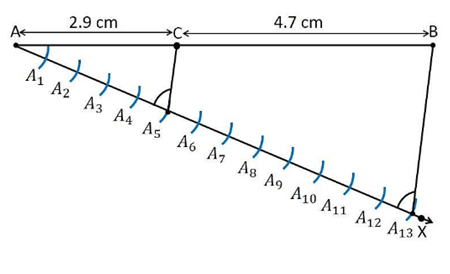
1. Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Construction Procedure:
A line segment with a measure of 7.6 cm length is divided in the ratio of 5:8 as follows.
1. Draw line segment AB with the length measure of 7.6 cm
2. Draw a ray AX that makes an acute angle with line segment AB.
3. Locate the points i.e.,13 (= 5+8) points, such as A1, A2, A3, A4 …….. A13, on the ray AX such that it becomes AA1 = A1A2 = A2A3 and so on.
4. Join the line segment and the ray, BA13.
5. Through the point A5, draw a line parallel to BA13 which makes an angle equal to ∠AA13B
6. The point A5 which intersects the line AB at point C.
7. C is the point divides line segment AB of 7.6 cm in the required ratio of 5:8.
8. Now, measure the lengths of the line AC and CB. It comes out to the measure of 2.9 cm and 4.7 cm respectively.
Justification:
The construction of the given problem can be justified by proving that
AC/CB = 5/ 8
By construction, we have A5C || A13B. From Basic proportionality theorem for the triangle AA13B, we get
AC/CB =AA5/A5A13….. (1)
From the figure constructed, it is observed that AA5 and A5A13 contain 5 and 8 equal divisions of line segments respectively.
Therefore, it becomes
AA5/A5A13=5/8… (2)
Compare the equations (1) and (2), we obtain
AC/CB = 5/ 8
Hence, Justified.
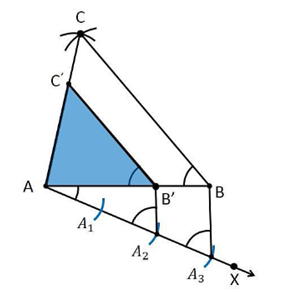
2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of
the corresponding sides of the first triangle.
Construction Procedure:
1. Draw a line segment AB which measures 4 cm, i.e., AB = 4 cm.
2. Take the point A as centre, and draw an arc of radius 5 cm.
3. Similarly, take the point B as its centre, and draw an arc of radius 6 cm.
4. The arcs drawn will intersect each other at point C.
5. Now, we obtained AC = 5 cm and BC = 6 cm and therefore ΔABC is the required triangle.
6. Draw a ray AX which makes an acute angle with the line segment AB on the opposite side of vertex C.
7. Locate 3 points such as A1, A2, A3 (as 3 is greater between 2 and 3) on line AX such that it becomes AA1= A1A2 = A2A3.
8. Join the point BA3 and draw a line through A2which is parallel to the line BA3 that intersect AB at point B’.
9. Through the point B’, draw a line parallel to the line BC that intersect the line AC at C’.
10. Therefore, ΔAB’C’ is the required triangle.
Justification:
The construction of the given problem can be justified by proving that
AB’ = (2/3)AB
B’C’ = (2/3)BC
AC’= (2/3)AC
From the construction, we get B’C’ || BC
∴ ∠AB’C’ = ∠ABC (Corresponding angles)
In ΔAB’C’ and ΔABC,
∠ABC = ∠AB’C (Proved above)
∠BAC = ∠B’AC’ (Common)
∴ ΔAB’C’ ∼ ΔABC (From AA similarity criterion)
Therefore, AB’/AB = B’C’/BC= AC’/AC …. (1)
In ΔAAB’ and ΔAAB,
∠A2AB’ =∠A3AB (Common)
From the corresponding angles, we get,
∠AA2B’ =∠AA3B
Therefore, from the AA similarity criterion, we obtain
ΔAA2B’ and AA3B
So, AB’/AB = AA2/AA3
Therefore, AB’/AB = 2/3 ……. (2)
From the equations (1) and (2), we get
AB’/AB=B’C’/BC = AC’/ AC = 2/3
This can be written as
AB’ = (2/3)AB
B’C’ = (2/3)BC
AC’= (2/3)AC
Hence, justified.
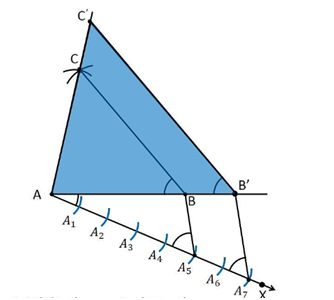
3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle
Construction Procedure:
1. Draw a line segment AB =5 cm.
2. Take A and B as centre, and draw the arcs of radius 6 cm and 5 cm respectively.
3. These arcs will intersect each other at point C and therefore ΔABC is the required triangle with the length of sides as 5 cm, 6 cm, and 7 cm respectively.
4. Draw a ray AX which makes an acute angle with the line segment AB on the opposite side of vertex C.
5. Locate the 7 points such as A1, A2, A3, A4, A5, A6, A7 (as 7 is greater between 5 and 7), on line AX such that it becomes AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A5A6 = A6A7
6. Join the points BA5 and draw a line from A7 to BA5 which is parallel to the line BA5 where it intersects the extended line segment AB at point B’.
7. Now, draw a line from B’ the extended line segment AC at C’ which is parallel to the line BC and it intersects to make a triangle.
8. Therefore, ΔAB’C’ is the required triangle.
Justification:
The construction of the given problem can be justified by proving that
AB’ = (7/5)AB
B’C’ = (7/5)BC
AC’= (7/5)AC
From the construction, we get B’C’ || BC
∴ ∠AB’C’ = ∠ABC (Corresponding angles)
In ΔAB’C’ and ΔABC,
∠ABC = ∠AB’C (Proved above)
∠BAC = ∠B’AC’ (Common)
∴ ΔAB’C’ ∼ ΔABC (From AA similarity criterion)
Therefore, AB’/AB = B’C’/BC= AC’/AC …. (1)
In ΔAA7B’ and ΔAA5B,
∠A7AB’=∠A5AB (Common)
From the corresponding angles, we get,
∠A A7B’=∠A A5B
Therefore, from the AA similarity criterion, we obtain
ΔA A2B’ and A A3B
So, AB’/AB = AA5/AA7
Therefore, AB /AB’ = 5/7 ……. (2)
From the equations (1) and (2), we get
AB’/AB = B’C’/BC = AC’/ AC = 7/5
This can be written as
AB’ = (7/5)AB
B’C’ = (7/5)BC
AC’= (7/5)AC
Hence, justified.

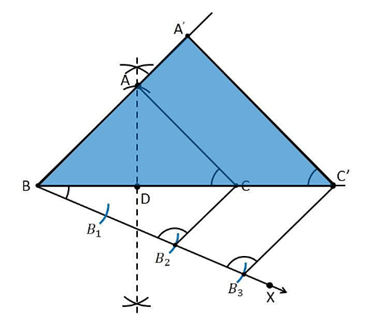
Construction Procedure:
1. Draw a line segment BC with the measure of 8 cm.
2. Now draw the perpendicular bisector of the line segment BC and intersect at the point D
3. Take the point D as centre and draw an arc with the radius of 4 cm which intersect the perpendicular bisector at the point A
4. Now join the lines AB and AC and the triangle is the required triangle.
5. Draw a ray BX which makes an acute angle with the line BC on the side opposite to the vertex A.
6. Locate the 3 points B1, B2 and B3 on the ray BX such that BB1 = B1B2 = B2B3
7. Join the points B2C and draw a line from B3 which is parallel to the line B2C where it intersects the extended line segment BC at point C’.
8. Now, draw a line from C’ the extended line segment AC at A’ which is parallel to the line AC and it intersects to make a triangle.
9. Therefore, ΔA’BC’ is the required triangle.
Justification:
The construction of the given problem can be justified by proving that
A’B = (3/2)AB
BC’ = (3/2)BC
A’C’= (3/2)AC
From the construction, we get A’C’ || AC
∴ ∠ A’C’B = ∠ACB (Corresponding angles)
In ΔA’BC’ and ΔABC,
∠B = ∠B (common)
∠A’BC’ = ∠ACB
∴ ΔA’BC’ ∼ ΔABC (From AA similarity criterion)
Therefore, A’B/AB = BC’/BC= A’C’/AC
Since the corresponding sides of the similar triangle are in the same ratio, it becomes
A’B/AB = BC’/BC= A’C’/AC = 3/2
Hence, justified.
5. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
Construction Procedure:
1. Draw a ΔABC with base side BC = 6 cm, and AB = 5 cm and ∠ABC = 60°.
2. Draw a ray BX which makes an acute angle with BC on the opposite side of vertex A.
3. Locate 4 points (as 4 is greater in 3 and 4), such as B1, B2, B3, B4, on line segment BX.
4. Join the points B4C and also draw a line through B3, parallel to B4C intersecting the line segment BC at C’.
5. Draw a line through C’ parallel to the line AC which intersects the line AB at A’.
6. Therefore, ΔA’BC’ is the required triangle.
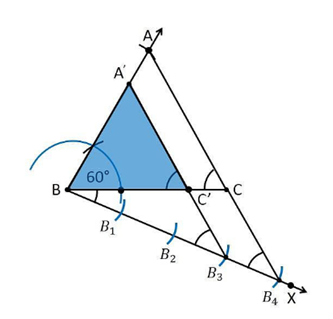
Justification:
The construction of the given problem can be justified by proving that
Since the scale factor is 3/4 , we need to prove
A’B = (3/4)AB
BC’ = (3/4)BC
A’C’= (3/4)AC
From the construction, we get A’C’ || AC
In ΔA’BC’ and ΔABC,
∴ ∠ A’C’B = ∠ACB (Corresponding angles)
∠B = ∠B (common)
∴ ΔA’BC’ ∼ ΔABC (From AA similarity criterion)
Since the corresponding sides of the similar triangle are in the same ratio, it becomes
Therefore, A’B/AB = BC’/BC= A’C’/AC
So, it becomes A’B/AB = BC’/BC= A’C’/AC = 3/4
Hence, justified.
6. Draw a triangle ABC with side BC = 7 cm, ∠ B = 45°, ∠ A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of ∆ ABC.
To find ∠C:
Given:
∠B = 45°, ∠A = 105°
We know that,
Sum of all interior angles in a triangle is 180°.
∠A+∠B +∠C = 180°
105°+45°+∠C = 180°
∠C = 180° − 150°
∠C = 30°
So, from the property of triangle, we get ∠C = 30°
Construction Procedure:
The required triangle can be drawn as follows.
1. Draw a ΔABC with side measures of base BC = 7 cm, ∠B = 45°, and ∠C = 30°.
2. Draw a ray BX makes an acute angle with BC on the opposite side of vertex A.
3. Locate 4 points (as 4 is greater in 4 and 3), such as B1, B2, B3, B4, on the ray BX.
4. Join the points B3C.
5. Draw a line through B4 parallel to B3C which intersects the extended line BC at C’.
6. Through C’, draw a line parallel to the line AC that intersects the extended line segment at C’.
7. Therefore, ΔA’BC’ is the required triangle.
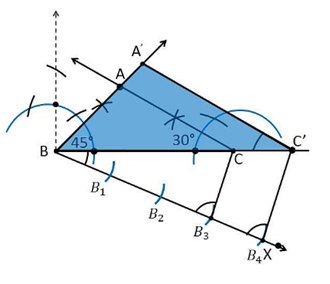
Justification:
The construction of the given problem can be justified by proving that
Since the scale factor is 4/3, we need to prove
A’B = (4/3)AB
BC’ = (4/3)BC
A’C’= (4/3)AC
From the construction, we get A’C’ || AC
In ΔA’BC’ and ΔABC,
∴ ∠A’C’B = ∠ACB (Corresponding angles)
∠B = ∠B (common)
∴ ΔA’BC’ ∼ ΔABC (From AA similarity criterion)
Since the corresponding sides of the similar triangle are in the same ratio, it becomes
Therefore, A’B/AB = BC’/BC= A’C’/AC
So, it becomes A’B/AB = BC’/BC= A’C’/AC = 4/3
Hence, justified.
7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Given:
The sides other than hypotenuse are of lengths 4cm and 3cm. It defines that the sides are perpendicular to each other
Construction Procedure:
The required triangle can be drawn as follows.
1. Draw a line segment BC =3 cm.
2. Now measure and draw ∠= 90°
3. Take B as centre and draw an arc with the radius of 4 cm and intersects the ray at the point B.
4. Now, join the lines AC and the triangle ABC is the required triangle.
5. Draw a ray BX makes an acute angle with BC on the opposite side of vertex A.
6. Locate 5 such as B1, B2, B3, B4, on the ray BX such that such that BB1 = B1B2 = B2B3= B3B4 = B4B5
7. Join the points B3C.
8. Draw a line through B5 parallel to B3C which intersects the extended line BC at C’.
9. Through C’, draw a line parallel to the line AC that intersects the extended line AB at A’.
10. Therefore, ΔA’BC’ is the required triangle.
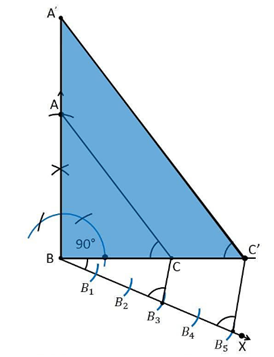
Justification:
The construction of the given problem can be justified by proving that
Since the scale factor is 5/3, we need to prove
A’B = (5/3)AB
BC’ = (5/3)BC
A’C’= (5/3)AC
From the construction, we get A’C’ || AC
In ΔA’BC’ and ΔABC,
∴ ∠ A’C’B = ∠ACB (Corresponding angles)
∠B = ∠B (common)
∴ ΔA’BC’ ∼ ΔABC (From AA similarity criterion)
Since the corresponding sides of the similar triangle are in the same ratio, it becomes
Therefore, A’B/AB = BC’/BC= A’C’/AC
So, it becomes A’B/AB = BC’/BC= A’C’/AC = 5/3
Hence, justified.