Exercise 7.3 Page No: 170
1.(#Coordinate Geometry)
Find the area of the triangle whose vertices are:
(i) (2, 3), (-1, 0), (2, -4)
(ii) (-5, -1), (3, -5), (5, 2)
Solution:
Area of a triangle formula =
(i) Here,
Substitute all the values in the above formula, we get
Area of triangle = 1/2 [2 {0- (-4)} + (-1) {(-4) – (3)} + 2 (3 – 0)]
= 1/2 {8 + 7 + 6} = 21/2
So area of triangle is 21/2 square units.
(ii) Here,
Area of the triangle = 1/2 [-5 { (-5)- (2)} + 3(2-(-1)) + 5{-1 – (-5)}]
= 1/2{35 + 9 + 20} = 32
Therefore, area of the triangle is 32 square units.
2.(#Coordinate Geometry)
In each of the following find the value of ‘k’, for which the points are collinear.
(i) (7, -2), (5, 1), (3, -k)
(ii) (8, 1), (k, -4), (2, -5)
Solution:
(i) For collinear points, area of triangle formed by them is always zero.
Let points (7, -2) (5, 1), and (3, k) are vertices of a triangle.
Area of triangle = 1/2 [7 { 1- k} + 5(k-(-2)) + 3{(-2) – 1}] = 0
7 – 7k + 5k +10 -9 = 0
-2k + 8 = 0
k = 4
(ii) For collinear points, area of triangle formed by them is zero.
Therefore, for points (8, 1), (k, – 4), and (2, – 5), area = 0
1/2 [8 { -4- (-5)} + k{(-5)-(1)} + 2{1 -(-4)}] = 0
8 – 6k + 10 = 0
6k = 18
k = 3
3.(#Coordinate Geometry)
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Solution:
Let the vertices of the triangle be A (0, -1), B (2, 1), C (0, 3).
Let D, E, F be the mid-points of the sides of this triangle.
Coordinates of D, E, and F are given by
D = ( , ) = (1, 0)
E = ( , ) = (0, 1)
F = ( , ) = (1, 2)
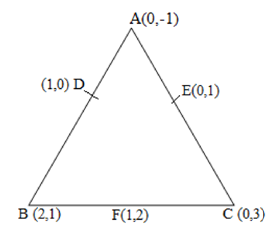
Area of a triangle =
Area of ΔDEF = 1/2 {1(2-1) + 1(1-0) + 0(0-2)} = 1/2 (1+1) = 1
Area of ΔDEF is 1 square units
Area of ΔABC = 1/2 [0(1-3) + 2{3-(-1)} + 0(-1-1)] = 1/2 {8} = 4
Area of ΔABC is 4 square units
Therefore, the required ratio is 1:4.
4.(#Coordinate Geometry)
Find the area of the quadrilateral whose vertices, taken in order, are
(-4, -2), (-3, -5), (3, -2) and (2, 3).
Solution:
Let the vertices of the quadrilateral be A (- 4, – 2), B ( – 3, – 5), C (3, – 2), and D (2, 3). Join AC and divide quadrilateral into two triangles.
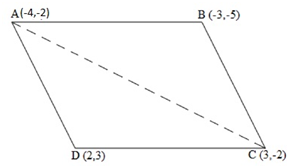
We have two triangles ΔABC and ΔACD.
Area of a triangle =
Area of ΔABC = 1/2 [(-4) {(-5) – (-2)} + (-3) {(-2) – (-2)} + 3 {(-2) – (-5)}]
= 1/2 (12 + 0 + 9)
= 21/2 square units
Area of ΔACD = 1/2 [(-4) {(-2) – (3)} + 3{(3) – (-2)} + 2 {(-2) – (-2)}]
= 1/2 (20 + 15 + 0)
= 35/2 square units
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD
= (21/2 + 35/2) square units = 28 square units
5.(#Coordinate Geometry)
You have studied in Class IX that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, – 6), B (3, – 2) and C (5, 2).
Solution:
Let the vertices of the triangle be A (4, -6), B (3, -2), and C (5, 2).
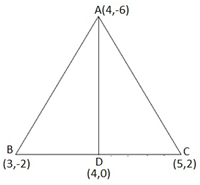
Let D be the mid-point of side BC of ΔABC. Therefore, AD is the median in ΔABC.
Coordinates of point D = Midpoint of BC = ( = (4, 0)
Formula, to find Area of a triangle =
Now, Area of ΔABD = 1/2 [(4) {(-2) – (0)} + 3{(0) – (-6)} + (4) {(-6) – (-2)}]
= 1/2 (-8 + 18 – 16)
= -3 square units
However, area cannot be negative. Therefore, area of ΔABD is 3 square units.
Area of ΔACD = 1/2 [(4) {0 – (2)} + 4{(2) – (-6)} + (5) {(-6) – (0)}]
= 1/2 (-8 + 32 – 30) = -3 square units
However, area cannot be negative. Therefore, area of ΔACD is 3 square units.
The area of both sides is same. Thus, median AD has divided ΔABC in two triangles of equal areas.