Chapter 6 Triangles – Part 1 Class 10 Maths

Introduction to Triangles

What is Triangle?

A triangle can be defined as a polygon which has three angles and three sides. The interior angles of a triangle sum up to 180 degrees and the exterior angles sum up to 360 degrees. Depending upon the angle and its length, a triangle can be categorized in the following types-

1. Scalene Triangle – All the three sides of the triangle are of different measure
2. Isosceles Triangle – Any two sides of the triangle are of equal length
3. Equilateral Triangle – All the three sides of a triangle are equal and each angle measures 60 degrees
4. Acute angled Triangle – All the angles are smaller than 90 degrees
5. Right angle Triangle – Anyone of the three angles is equal to 90 degrees
6. Obtuse-angled Triangle – One of the angles is greater than 90 degrees

Similarity Criteria of Two Polygons Having the Same Number of Sides

Any two polygons which have the same number of sides are similar if the following two criteria are met-

1. Their corresponding angles are equal, and
2. Their corresponding sides are in the same ratio (or proportion)

Similarity Criteria of Triangles

To find whether the given two triangles are similar or not, it has four criteria. They are:

• Side-Side- Side (SSS) Similarity Criterion – When the corresponding sides of any two triangles are in the same ratio, then their corresponding angles will be equal and the triangle will be considered as similar triangles.
• Angle Angle Angle (AAA) Similarity Criterion – When the corresponding angles of any two triangles are equal, then their corresponding side will be in the same ratio and the triangles are considered to be similar.
• Angle-Angle (AA) Similarity Criterion – When two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are considered as similar.
• Side-Angle-Side (SAS) Similarity Criterion – When one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio (proportional), then the triangles are said to be similar.

Proof of Pythagoras Theorem

Statement: As per Pythagoras theorem, “In a right-angled triangle, the sum of squares of two sides of a right triangle is equal to the square of the hypotenuse of the triangle.”

Proof –

Consider the right triangle, right-angled at B.

Construction-

Draw BD ⊥ AC

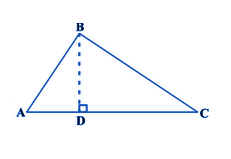
Now,  △ADC ~ △ABC

So, AD/AB = AB/AC

or AD. AC = AB² ……………(i)

Also, △BCD ~ △ ABC

So, CD/BC = BC/AC

or, CD. AC = BC² ……………(ii)

Adding (i) and (ii),

AD. AC + CD. AC = AB² + BC²

AC(AD + DC) = AB² + BC²

AC(AC) = AB² + BC²

⇒ AC² = AB² + BC²

Hence, proved.

Solved Example

Question:

In a right-angled triangle ABC, which is right-angled at A, where CM and BL are the medians of a triangle. Show that, 4(BL² +CM²) = 5 BC²

Solution:

Given that,

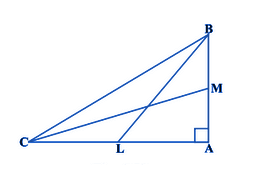
Medians BL and CM,  ∠A = 90°

From the triangle ABC, we can write it as:

BC² = AB² + AC² (Using Pythagoras Theorem) …(1)

From the triangle, ABL,

BL² = AL² +AB²

or we can write the above equation as:

BL² =(AC/2)² +AB² (Where L is the midpoint of AC)

BL² = (AC²/4) + AB²

4BL² = AC² + 4 AB² ….(2)

From triangle CMA,

CM² = AC² + AM²

CM² = AC² + (AB/2)² (Where M is the midpoint of AB)

CM² = AC² + AB²/4

4CM = 4 AC +AB ….(3)

Now, by adding (2) and (3), we  get,

4(BL²+ CM²) = 5(AC²+ AB²)

Using equation (1), we can write it as:

4(BL²+ CM²) = 5 BC²

Hence, it is proved.

Problems Related to Triangles

1. A girl having a height of 90 cm is walking away from a lamp-post’s base at a speed of 1.2 m/s. Calculate the length of that girl’s shadow after 4 seconds if the lamp is 3.6 m above the ground.
2. S and T are points on sides PR and QR of triangle PQR such that angle P = angle RTS. Now, prove that triangle RPQ and triangle RTS are similar.
3. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD
   at F. Show that triangles ABE and CFB are similar.