Exercise: 12.3 (Page No: 234)
1. Find the area of the shaded region in Fig. 12.19, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.

Solution:
Here, P is in the semi-circle and so,
P = 90°
So, it can be concluded that QR is hypotenuse of the circle and is equal to the diameter of the circle.
∴ QR = D
Using Pythagorean theorem,
QR2 = PR2+PQ2
Or, QR2 = 72+242
QR= 25 cm = Diameter
Hence, the radius of the circle = 25/2 cm
Now, the area of the semicircle = (πR2)/2
= (22/7)×(25/2)×(25/2)/2 cm2
= 13750/56 cm2 = 245.54 cm2
Also, area of the ΔPQR = ½×PR×PQ
=(½)×7×24 cm2
= 84 cm2
Hence, the area of the shaded region = 245.54 cm2-84 cm2
= 161.54 cm2
2. Find the area of the shaded region in Fig. 12.20, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and AOC = 40°.
Solution:

Given,
Angle made by sector = 40°,
Radius the inner circle = r = 7 cm, and
Radius of the outer circle = R = 14 cm
We know,
Area of the sector = (θ/360°)×πr2
So, Area of OAC = (40°/360°)×πr2 cm2
= 68.44 cm2
Area of the sector OBD = (40°/360°)×πr2 cm2
= (1/9)×(22/7)×72 = 17.11 cm2
Now, area of the shaded region ABDC = Area of OAC – Area of the OBD
= 68.44 cm2 – 17.11 cm2 = 51.33 cm2
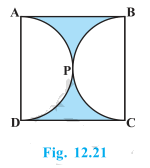
3. Find the area of the shaded region in Fig. 12.21, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
Solution:
Side of the square ABCD (as given) = 14 cm
So, Area of ABCD = a2
= 14×14 cm2 = 196 cm2
We know that the side of the square = diameter of the circle = 14 cm
So, side of the square = diameter of the semicircle = 14 cm
∴ Radius of the semicircle = 7 cm
Now, area of the semicircle = (πR2)/2
= (22/7×7×7)/2 cm2 =
= 77 cm2
∴ Area of two semicircles = 2×77 cm2 = 154 cm2
Hence, area of the shaded region = Area of the Square – Area of two semicircles
= 196 cm2 -154 cm2
= 42 cm2
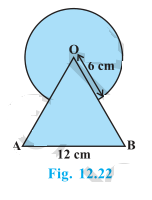
4. Find the area of the shaded region in Fig. 12.22, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
Solution:
It is given that OAB is an equilateral triangle having each angle as 60°
Area of the sector is common in both.
Radius of the circle = 6 cm.
Side of the triangle = 12 cm.
Area of the equilateral triangle = (√3/4) (OA)2= (√3/40×122 = 36√3 cm2
Area of the circle = πR2 = (22/7)×62 = 792/7 cm2
Area of the sector making angle 60° = (60°/360°) ×πr2 cm2
= (1/6)×(22/7)× 62 cm2 = 132/7 cm2
Area of the shaded region = Area of the equilateral triangle + Area of the circle – Area of the sector
= 36√3 cm2 +792/7 cm2-132/7 cm2
= (36√3+660/7) cm2
5. From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
Solution:
Side of the square = 4 cm
Radius of the circle = 1 cm
Four quadrant of a circle are cut from corner and one circle of radius are cut from middle.
Area of square = (side)2= 42 = 16 cm2
Area of the quadrant = (πR2)/4 cm2 = (22/7)×(12)/4 = 11/14 cm2
∴ Total area of the 4 quadrants = 4 ×(11/14) cm2 = 22/7 cm2
Area of the circle = πR2 cm2 = (22/7×12) = 22/7 cm2
Area of the shaded region = Area of square – (Area of the 4 quadrants + Area of the circle)
= 16 cm2-(22/7) cm2+(22/7) cm2
= 68/7 cm2
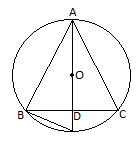
6. In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design.

Solution:
Radius of the circle = 32 cm
Draw a median AD of the triangle passing through the centre of the circle.
⇒ BD = AB/2
Since, AD is the median of the triangle
∴ AO = Radius of the circle = (2/3) AD
⇒ (2/3)AD = 32 cm
⇒ AD = 48 cm
In ΔADB,
By Pythagoras theorem,
AB2 = AD2 +BD2
⇒ AB2 = 482+(AB/2)2
⇒ AB2 = 2304+AB2/4
⇒ 3/4 (AB2)= 2304
⇒ AB2 = 3072
⇒ AB= 32√3 cm
Area of ΔADB = √3/4 ×(32√3)2 cm2 = 768√3 cm2
Area of circle = πR2 = (22/7)×32×32 = 22528/7 cm2
Area of the design = Area of circle – Area of ΔADB
= (22528/7 – 768√3) cm2
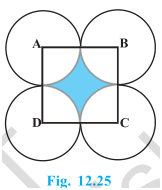
7. In Fig. 12.25, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
Solution:
Side of square = 14 cm
Four quadrants are included in the four sides of the square.
∴ Radius of the circles = 14/2 cm = 7 cm
Area of the square ABCD = 142 = 196 cm2
Area of the quadrant = (πR2)/4 cm2 = (22/7) ×72/4 cm2
= 77/2 cm2
Total area of the quadrant = 4×77/2 cm2 = 154cm2
Area of the shaded region = Area of the square ABCD – Area of the quadrant
= 196 cm2 – 154 cm2
= 42 cm2
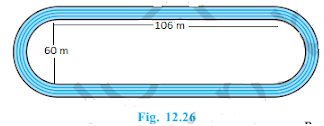
8. Fig. 12.26 depicts a racing track whose left and right ends are semicircular.
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) the distance around the track along its inner edge
(ii) the area of the track.
Solution:
Width of the track = 10 m
Distance between two parallel lines = 60 m
Length of parallel tracks = 106 m

DE = CF = 60 m
Radius of inner semicircle, r = OD = O’C
= 60/2 m = 30 m
Radius of outer semicircle, R = OA = O’B
= 30+10 m = 40 m
Also, AB = CD = EF = GH = 106 m
Distance around the track along its inner edge = CD+EF+2×(Circumference of inner semicircle)
= 106+106+(2×πr) m = 212+(2×22/7×30) m
= 212+1320/7 m = 2804/7 m
Area of the track = Area of ABCD + Area EFGH + 2 × (area of outer semicircle) – 2 × (area of inner semicircle)
= (AB×CD)+(EF×GH)+2×(πr2/2) -2×(πR2/2) m2
= (106×10)+(106×10)+2×π/2(r2-R2) m2
= 2120+22/7×70×10 m2
= 4320 m2
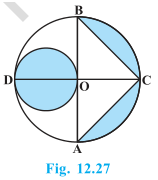
9. In Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Solution:
Radius of larger circle, R = 7 cm
Radius of smaller circle, r = 7/2 cm
Height of ΔBCA = OC = 7 cm
Base of ΔBCA = AB = 14 cm
Area of ΔBCA = 1/2 × AB × OC = (½)×7×14 = 49 cm2
Area of larger circle = πR2 = (22/7)×72 = 154 cm2
Area of larger semicircle = 154/2 cm2 = 77 cm2
Area of smaller circle = πr2 = (22/7)×(7/2)×(7/2) = 77/2 cm2
Area of the shaded region = Area of larger circle – Area of triangle – Area of larger semicircle + Area of smaller circle
Area of the shaded region = (154-49-77+77/2) cm2
= 133/2 cm2 = 66.5 cm2
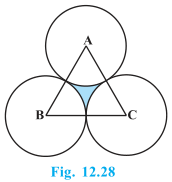
10. The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region. (Use π = 3.14 and √3 = 1.73205)
Solution:
ABC is an equilateral triangle.
∴ ∠ A = ∠ B = ∠ C = 60°
There are three sectors each making 60°.
Area of ΔABC = 17320.5 cm2
⇒ √3/4 ×(side)2 = 17320.5
⇒ (side)2 =17320.5×4/1.73205
⇒ (side)2 = 4×104
⇒ side = 200 cm
Radius of the circles = 200/2 cm = 100 cm
Area of the sector = (60°/360°)×π r2 cm2
= 1/6×3.14×(100)2 cm2
= 15700/3cm2
Area of 3 sectors = 3×15700/3 = 15700 cm2
Thus, area of the shaded region = Area of equilateral triangle ABC – Area of 3 sectors
= 17320.5-15700 cm2 = 1620.5 cm2
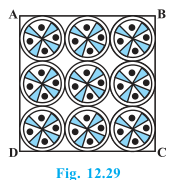
11. On a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig. 12.29). Find the area of the remaining portion of the handkerchief.
Solution:
Number of circular designs = 9
Radius of the circular design = 7 cm
There are three circles in one side of square handkerchief.
∴ Side of the square = 3×diameter of circle = 3×14 = 42 cm
Area of the square = 42×42 cm2 = 1764 cm2
Area of the circle = π r2 = (22/7)×7×7 = 154 cm2
Total area of the design = 9×154 = 1386 cm2
Area of the remaining portion of the handkerchief = Area of the square – Total area of the design = 1764 – 1386 = 378 cm2
12. In Fig. 12.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.
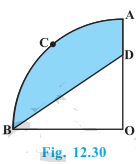
Solution:
Radius of the quadrant = 3.5 cm = 7/2 cm
(i) Area of quadrant OACB = (πR2)/4 cm2
= (22/7)×(7/2)×(7/2)/4 cm2
= 77/8 cm2
(ii) Area of triangle BOD = (½)×(7/2)×2 cm2
= 7/2 cm2
Area of shaded region = Area of quadrant – Area of triangle BOD
= (77/8)-(7/2) cm2 = 49/8 cm2
= 6.125 cm2
13. In Fig. 12.31, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
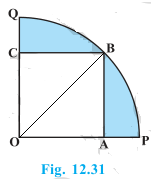
Solution:
Side of square = OA = AB = 20 cm
Radius of the quadrant = OB
OAB is right angled triangle
By Pythagoras theorem in ΔOAB,
OB2 = AB2+OA2
⇒ OB2 = 202 +202
⇒ OB2 = 400+400
⇒ OB2 = 800
⇒ OB= 20√2 cm
Area of the quadrant = (πR2)/4 cm2 = (3.14/4)×(20√2)2 cm2 = 628cm2
Area of the square = 20×20 = 400 cm2
Area of the shaded region = Area of the quadrant – Area of the square
= 628-400 cm2 = 228cm2
14. AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig. 12.32). If ∠AOB = 30°, find the area of the shaded region.
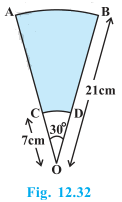
Solution:
Radius of the larger circle, R = 21 cm
Radius of the smaller circle, r = 7 cm
Angle made by sectors of both concentric circles = 30°
Area of the larger sector = (30°/360°)×πR2 cm2
= (1/12)×(22/7)×212 cm2
= 231/2cm2
Area of the smaller circle = (30°/360°)×πr2 cm2
= 1/12×22/7×72 cm2
=77/6 cm2
Area of the shaded region = (231/2) – (77/6) cm2
= 616/6 cm2 = 308/3cm2
15. In Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
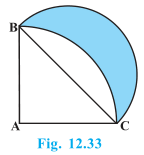
Solution:
Radius of the quadrant ABC of circle = 14 cm
AB = AC = 14 cm
BC is diameter of semicircle.
ABC is right angled triangle.
By Pythagoras theorem in ΔABC,
BC2 = AB2 +AC2
⇒ BC2 = 142 +142
⇒ BC = 14√2 cm
Radius of semicircle = 14√2/2 cm = 7√2 cm
Area of ΔABC =( ½)×14×14 = 98 cm2
Area of quadrant = (¼)×(22/7)×(14×14) = 154 cm2
Area of the semicircle = (½)×(22/7)×7√2×7√2 = 154 cm2
Area of the shaded region =Area of the semicircle + Area of ΔABC – Area of quadrant
= 154 +98-154 cm2 = 98cm2
16. Calculate the area of the designed region in Fig. 12.34 common between the two quadrants of circles of radius 8 cm each.
Solution:
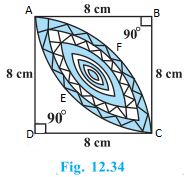
AB = BC = CD = AD = 8 cm
Area of ΔABC = Area of ΔADC = (½)×8×8 = 32 cm2
Area of quadrant AECB = Area of quadrant AFCD = (¼)×22/7×82
= 352/7 cm2
Area of shaded region = (Area of quadrant AECB – Area of ΔABC) = (Area of quadrant AFCD – Area of ΔADC)
= (352/7 -32)+(352/7- 32) cm2
= 2×(352/7-32) cm2
= 256/7 cm2