Exercise 9.3 Page: 162
1. In Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar(ACE).
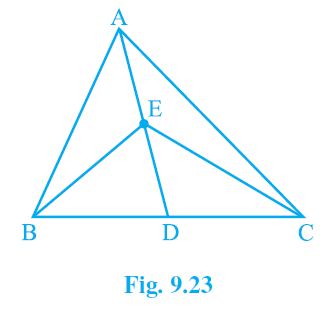
Solution:
Given,
AD is median of ΔABC. ∴, it will divide ΔABC into two triangles of equal area.
∴ar(ABD) = ar(ACD) — (i)
also,
ED is the median of ΔABC.
∴ar(EBD) = ar(ECD) — (ii)
Subtracting (ii) from (i),
ar(ABD) – ar(EBD) = ar(ACD) – ar(ECD)
⇒ar(ABE) = ar(ACE)
2. In a triangle ABC, E is the mid-point of median AD. Show that ar(BED) = ¼ ar(ABC).
Solution:

ar(BED) = (1/2)×BD×DE
Since, E is the mid-point of AD,
AE = DE
Since, AD is the median on side BC of triangle ABC,
BD = DC
,
DE = (1/2) AD — (i)
BD = (1/2)BC — (ii)
From (i) and (ii), we get,
ar(BED) = (1/2)×(1/2)BC × (1/2)AD
⇒ ar(BED) = (1/2)×(1/2)ar(ABC)
⇒ ar(BED) = ¼ ar(ABC)
3. Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Solution:
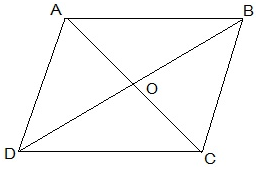
O is the mid point of AC and BD. (diagonals of bisect each other)
In ΔABC, BO is the median.
∴ar(AOB) = ar(BOC) — (i)
also,
In ΔBCD, CO is the median.
∴ar(BOC) = ar(COD) — (ii)
In ΔACD, OD is the median.
∴ar(AOD) = ar(COD) — (iii)
In ΔABD, AO is the median.
∴ar(AOD) = ar(AOB) — (iv)
From equations (i), (ii), (iii) and (iv), we get,
ar(BOC) = ar(COD) = ar(AOD) = ar(AOB)
Hence, we get, the diagonals of a parallelogram divide it into four triangles of equal area.
4. In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that: ar(ABC) = ar(ABD).

Solution:
In ΔABC, AO is the median. (CD is bisected by AB at O)
∴ar(AOC) = ar(AOD) — (i)
also,
ΔBCD, BO is the median. (CD is bisected by AB at O)
∴ar(BOC) = ar(BOD) — (ii)
Adding (i) and (ii),
We get,
ar(AOC)+ar(BOC) = ar(AOD)+ar(BOD)
⇒ar(ABC) = ar(ABD)
5. D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC.
Show that
(i) BDEF is a parallelogram.
(ii) ar(DEF) = ¼ ar(ABC)
(iii) ar (BDEF) = ½ ar(ABC)
Solution:

(i) In ΔABC,
EF || BC and EF = ½ BC (by mid point theorem)
also,
BD = ½ BC (D is the mid point)
So, BD = EF
also,
BF and DE are parallel and equal to each other.
∴, the pair opposite sides are equal in length and parallel to each other.
∴ BDEF is a parallelogram.
(ii) Proceeding from the result of (i),
BDEF, DCEF, AFDE are parallelograms.
Diagonal of a parallelogram divides it into two triangles of equal area.
∴ar(ΔBFD) = ar(ΔDEF) (For parallelogram BDEF) — (i)
also,
ar(ΔAFE) = ar(ΔDEF) (For parallelogram DCEF) — (ii)
ar(ΔCDE) = ar(ΔDEF) (For parallelogram AFDE) — (iii)
From (i), (ii) and (iii)
ar(ΔBFD) = ar(ΔAFE) = ar(ΔCDE) = ar(ΔDEF)
⇒ ar(ΔBFD) +ar(ΔAFE) +ar(ΔCDE) +ar(ΔDEF) = ar(ΔABC)
⇒ 4 ar(ΔDEF) = ar(ΔABC)
⇒ ar(DEF) = ¼ ar(ABC)
(iii) Area (parallelogram BDEF) = ar(ΔDEF) +ar(ΔBDE)
⇒ ar(parallelogram BDEF) = ar(ΔDEF) +ar(ΔDEF)
⇒ ar(parallelogram BDEF) = 2× ar(ΔDEF)
⇒ ar(parallelogram BDEF) = 2× ¼ ar(ΔABC)
⇒ ar(parallelogram BDEF) = ½ ar(ΔABC)
6. In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD.
If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint : From D and B, draw perpendiculars to AC.]

Solution:

Given,
OB = OD and AB = CD
Construction,
DE ⊥ AC and BF ⊥ AC are drawn.
Proof:
(i) In ΔDOE and ΔBOF,
∠DEO = ∠BFO (Perpendiculars)
∠DOE = ∠BOF (Vertically opposite angles)
OD = OB (Given)
∴, ΔDOE ≅ ΔBOF by AAS congruence condition.
∴, DE = BF (By CPCT) — (i)
also, ar(ΔDOE) = ar(ΔBOF) (Congruent triangles) — (ii)
Now,
In ΔDEC and ΔBFA,
∠DEC = ∠BFA (Perpendiculars)
CD = AB (Given)
DE = BF (From i)
∴, ΔDEC ≅ ΔBFA by RHS congruence condition.
∴, ar(ΔDEC) = ar(ΔBFA) (Congruent triangles) — (iii)
Adding (ii) and (iii),
ar(ΔDOE) + ar(ΔDEC) = ar(ΔBOF) + ar(ΔBFA)
⇒ ar (DOC) = ar (AOB)
(ii) ar(ΔDOC) = ar(ΔAOB)
Adding ar(ΔOCB) in LHS and RHS, we get,
⇒ar(ΔDOC) + ar(ΔOCB) = ar(ΔAOB) + ar(ΔOCB)
⇒ ar(ΔDCB) = ar(ΔACB)
(iii) When two triangles have same base and equal areas, the triangles will be in between the same parallel lines
ar(ΔDCB) = ar(ΔACB)
DA || BC — (iv)
For quadrilateral ABCD, one pair of opposite sides are equal (AB = CD) and other pair of opposite sides are parallel.
∴, ABCD is parallelogram.
7. D and E are points on sides AB and AC respectively of ΔABC such that ar(DBC) = ar(EBC). Prove that DE || BC.
Solution:

ΔDBC and ΔEBC are on the same base BC and also having equal areas.
∴, they will lie between the same parallel lines.
∴, DE || BC.
8. XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that
ar(ΔABE) = ar(ΔACF)
Solution:
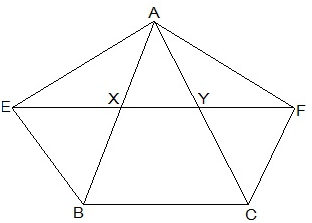
Given,
XY || BC, BE || AC and CF || AB
To show,
ar(ΔABE) = ar(ΔAC)
Proof:
BCYE is a || gm as ΔABE and ||gm BCYE are on the same base BE and between the same parallel lines BE and AC.
∴,ar(ABE) = ½ ar(BCYE) … (1)
Now,
CF || AB and XY || BC
⇒ CF || AB and XF || BC
⇒ BCFX is a || gm
As ΔACF and || gm BCFX are on the same base CF and in-between the same parallel AB and FC .
∴,ar (ΔACF)= ½ ar (BCFX) … (2)
But,
||gm BCFX and || gm BCYE are on the same base BC and between the same parallels BC and EF.
∴,ar (BCFX) = ar(BCYE) … (3)
From (1) , (2) and (3) , we get
ar (ΔABE) = ar(ΔACF)
⇒ ar(BEYC) = ar(BXFC)
As the parallelograms are on the same base BC and in-between the same parallels EF and BC–(iii)
Also,
△AEB and ||gm BEYC are on the same base BE and in-between the same parallels BE and AC.
⇒ ar(△AEB) = ½ ar(BEYC) — (iv)
Similarly,
△ACF and || gm BXFC on the same base CF and between the same parallels CF and AB.
⇒ ar(△ ACF) = ½ ar(BXFC) — (v)
From (iii), (iv) and (v),
ar(△ABE) = ar(△ACF)
9. The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see Fig. 9.26). Show that
ar(ABCD) = ar(PBQR).
[Hint : Join AC and PQ. Now compare ar(ACQ) and ar(APQ).]
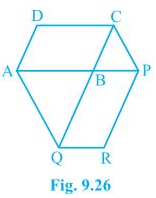
Solution:

AC and PQ are joined.
Ar(△ACQ) = ar(△APQ) (On the same base AQ and between the same parallel lines AQ and CP)
⇒ ar(△ACQ)-ar(△ABQ) = ar(△APQ)-ar(△ABQ)
⇒ ar(△ABC) = ar(△QBP) — (i)
AC and QP are diagonals ABCD and PBQR.
∴,ar(ABC) = ½ ar(ABCD) — (ii)
ar(QBP) = ½ ar(PBQR) — (iii)
From (ii) and (ii),
½ ar(ABCD) = ½ ar(PBQR)
⇒ ar(ABCD) = ar(PBQR)
10. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
Solution:

△DAC and △DBC lie on the same base DC and between the same parallels AB and CD.
Ar(△DAC) = ar(△DBC)
⇒ ar(△DAC) – ar(△DOC) = ar(△DBC) – ar(△DOC)
⇒ ar(△AOD) = ar(△BOC)
11. In Fig. 9.27, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F.
Show that
(i) ar(△ACB) = ar(△ACF)
(ii) ar(AEDF) = ar(ABCDE)

Solution:
- △ACB and △ACF lie on the same base AC and between the same parallels AC and BF.
∴ar(△ACB) = ar(△ ACF)
- ar(△ACB) = ar(△ACF)
⇒ ar(△ACB)+ar(△ACDE) = ar(△ACF)+ar(△ACDE)
⇒ ar(ABCDE) = ar(△AEDF)
12. A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Solution:

Let ABCD be the plot of the land of the shape of a quadrilateral.

To Construct,
Join the diagonal BD.
Draw AE parallel to BD.
Join BE, that intersected AD at O.
We get,
△BCE is the shape of the original field
△AOB is the area for constructing health centre.
△DEO is the land joined to the plot.
To prove:
ar(△DEO) = ar(△AOB)
Proof:
△DEB and △DAB lie on the same base BD, in-between the same parallels BD and AE.
Ar(△DEB) = ar(△DAB)
⇒ar(△DEB) – ar△DOB) = ar(△DAB) – ar(△DOB)
⇒ ar(△DEO) = ar(△AOB)
13. ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (△ADX) = ar (△ACY).
[Hint : Join CX.]
Solution:
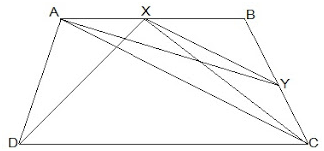
Given,
ABCD is a trapezium with AB || DC.
XY || AC
Construction,
Join CX
To Prove,
ar(ADX) = ar(ACY)
Proof:
ar(△ADX) = ar(△AXC) — (i) (Since they are on the same base AX and in-between the same parallels AB and CD)
also,
ar(△ AXC)=ar(△ ACY) — (ii) (Since they are on the same base AC and in-between the same parallels XY and AC.)
(i) and (ii),
ar(△ADX) = ar(△ACY)
14. In Fig.9.28, AP || BQ || CR. Prove that ar(△AQC) = ar(△PBR).

Solution:
Given,
AP || BQ || CR
To Prove,
ar(AQC) = ar(PBR)
Proof:
ar(△AQB) = ar(△PBQ) — (i) (Since they are on the same base BQ and between the same parallels AP and BQ.)
also,
ar(△BQC) = ar(△BQR) — (ii) (Since they are on the same base BQ and between the same parallels BQ and CR.)
Adding (i) and (ii),
ar(△AQB)+ar(△BQC) = ar(△PBQ)+ar(△BQR)
⇒ ar(△ AQC) = ar(△ PBR)
15. Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(△AOD) = ar(△BOC). Prove that ABCD is a trapezium.
Solution:

Given,
ar(△AOD) = ar(△BOC)
To Prove,
ABCD is a trapezium.
Proof:
ar(△AOD) = ar(△BOC)
⇒ ar(△AOD) + ar(△AOB) = ar(△BOC)+ar(△AOB)
⇒ ar(△ADB) = ar(△ACB)
Areas of △ADB and △ACB are equal. ∴, they must lying between the same parallel lines.
∴, AB ∥ CD
∴, ABCD is a trapezium.
16. In Fig.9.29, ar(DRC) = ar(DPC) and ar(BDP) = ar(ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
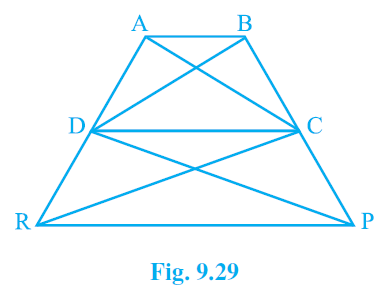
Solution:
Given,
ar(△DRC) = ar(△DPC)
ar(△BDP) = ar(△ARC)
To Prove,
ABCD and DCPR are trapeziums.
Proof:
ar(△BDP) = ar(△ARC)
⇒ ar(△BDP) – ar(△DPC) = ar(△DRC)
⇒ ar(△BDC) = ar(△ADC)
ar(△BDC) = ar(△ADC).
∴, ar(△BDC) and ar(△ADC) are lying in-between the same parallel lines.
∴, AB ∥ CD
ABCD is a trapezium.
Similarly,
ar(△DRC) = ar(△DPC).
∴, ar(△DRC) andar(△DPC) are lying in-between the same parallel lines.
∴, DC ∥ PR
∴, DCPR is a trapezium.