Introduction of Quadrilaterals Notes
Parallelogram: Opposite sides of a parallelogram are equal
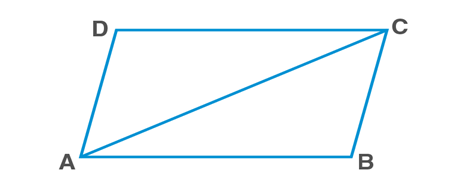
In ΔABC and ΔCDA
AC=AC [Common / transversal]
∠BCA=∠DAC [alternate angles]
∠BAC=∠DCA [alternate angles]
ΔABC≅ΔCDA [ASA rule]
Hence,
AB=DC and AD=BC [ C.P.C.T.C]Opposite angles in a parallelogram are equal
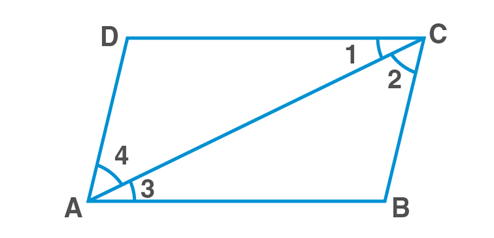
In parallelogram ABCD
AB‖CD; and AC is the transversal
Hence, ∠1=∠3….(1) (alternate interior angles)
BC‖DA; and AC is the transversal
Hence, ∠2=∠4….(2) (alternate interior angles)
Adding (1) and (2)
∠1+∠2=∠3+∠4
∠BAD=∠BCD
Similarly,
∠ADC=∠ABC
Properties of diagonal of a parallelogram
– Diagonals of a parallelogram bisect each other.
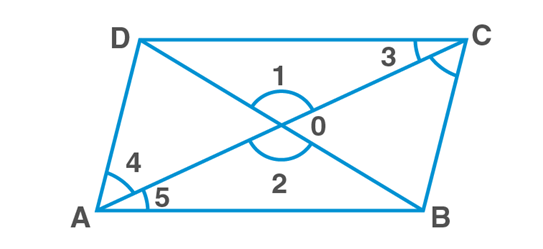
In ΔAOB and ΔCOD,
∠3=∠5 [alternate interior angles]
∠1=∠2 AB=CD [opp. Sides of parallelogram]
ΔAOB≅ΔCOD [AAS rule]
OB=OD and OA=OC [C.P.C.T]
Hence, proved
Conversely,
– If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
– Diagonal of a parallelogram divides it into two congruent triangles.
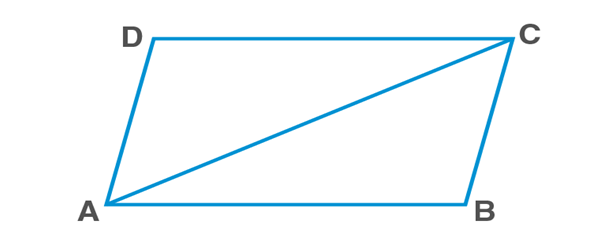
In ΔABC and ΔCDA,
AB=CD [Opposite sides of parallelogram]
BC=AD [Opposite sides of parallelogram]
AC=AC [Common side]
ΔABC≅ΔCDA [by SSS rule]
Hence, proved
Diagonals of a rhombus bisect each other at right angles
Diagonals of a rhombus bisect each – other at right angles
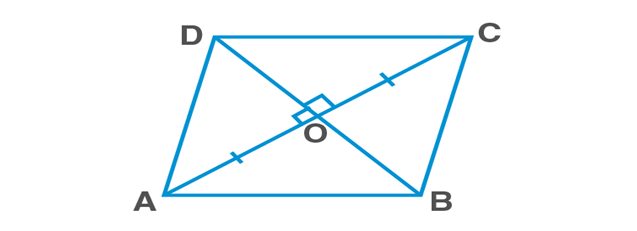
In ΔAOD and ΔCOD,
OA=OC [Diagonals of parallelogram bisect each other]
OD=OD [Common side]
AD=CD [Adjacent sides of a rhombus]
ΔAOD≅ΔCOD [SSS rule]
∠AOD=∠DOC [C.P.C.T]
∠AOD+∠DOC=180 [∵ AOC is a straight line]
Hence, ∠AOD=∠DOC=90
Hence proved
Diagonals of a rectangle bisect each other and are equal
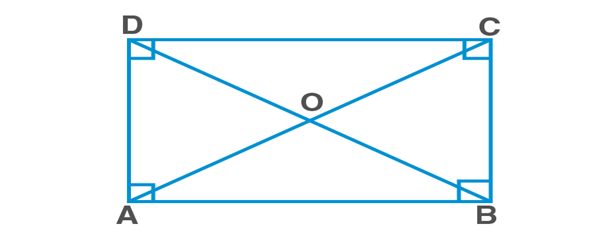
Rectangle ABCD
In ΔABC and ΔBAD,
AB=BA [Common side]
BC=AD [Opposite sides of a rectangle]
∠ABC=∠BAD [Each = 900 ∵ ABCD is a Rectangle]
ΔABC≅ΔBAD [SAS rule]
∴AC=BD [C.P.C.T]
Consider ΔOAD and ΔOCB,
AD=CB [Opposite sides of a rectangle]
∠OAD=∠OCB [∵ AD||BC and transversal AC intersects them]
∠ODA=∠OBC [∵ AD||BC and transversal BD intersects them]
ΔOAD≅ΔOCB [ASA rule]
∴OA=OC [C.P.C.T]
Similarly we can prove OB=OD
Diagonals of a square bisect each other at right angles and are equal
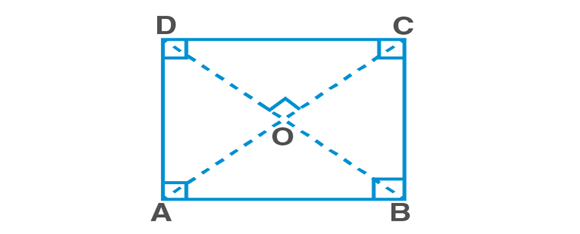
Square ABCD
In ΔABC and ΔBAD,
AB=BA [Common side]
BC=AD [Opposite sides of a Square]
∠ABC=∠BAD [Each = 900 ∵ ABCD is a Square]
ΔABC≅ΔBAD [SAS rule]
∴AC=BD [C.P.C.T]
Consider ΔOAD and ΔOCB,
AD=CB [Opposite sides of a Square]
∠OAD=∠OCB [∵ AD||BC and transversal AC intersects them]
∠ODA=∠OBC [∵ AD||BC and transversal BD intersects them]
ΔOAD≅ΔOCB [ASA rule]
∴OA=OC [C.P.C.T]
Similarly we can prove OB=OD
In ΔOBA and ΔODA,
OB=OD [ proved above]
BA=DA [Sides of a Square]
OA=OA [ Common side]
ΔOBA≅ΔODA, [ SSS rule]
∴∠AOB=∠AOD [ C.P.C.T]
But, ∠AOB+∠AOD=1800 [ Linear pair]
∴∠AOB=∠AOD=900
Important results related to parallelograms

Parallelogram ABCD
Opposite sides of a parallelogram are parallel and equal.
AB||CD,AD||BC,AB=CD,AD=BC
Opposite angles of a parallelogram are equal adjacent angels are supplementary.
∠A=∠C,∠B=∠D,
∠A+∠B=1800,∠B+∠C=1800,∠C+∠D=1800,∠D+∠A=1800
A diagonal of parallelogram divides it into two congruent triangles.
ΔABC≅ΔCDA [With respect to AC as diagonal]
ΔADB≅ΔCBD [With respect to BD as diagonal]
The diagonals of a parallelogram bisect each other.
AE=CE,BE=DE
∠1=∠5 (alternate interior angles)
∠2=∠6 (alternate interior angles)
∠3=∠7 (alternate interior angles)
∠4=∠8 (alternate interior angles)
∠9=∠11 (vertically opp. angles)
∠10=∠12 (vertically opp. angles)
The Mid-Point Theorem
The line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half of the third side
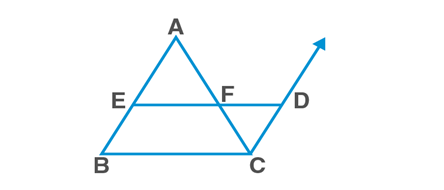
In ΔABC, E – the midpoint of AB; F – the midpoint of AC
Construction: Produce EF to D such that EF=DF.
In ΔAEF and ΔCDF,
AF=CF [ F is the midpoint of AC]
∠AFE=∠CFD [ V.O.A]
EF=DF [ Construction]
∴ΔAEF≅ΔCDF [SAS rule]
Hence,
∠EAF=∠DCF….(1)
DC=EA=EB [ E is the midpoint of AB]
DC‖EA‖AB [Since, (1), alternate interior angles]
DC‖EB
So EBCD is a parallelogram
Therefore, BC=ED and BC‖ED
Since, ED=EF+FD=2EF=BC [ ∵ EF=FD]
We have,EF=12BC and EF||BC
Hence proved
Introduction to Quadrilaterals
Quadrilaterals
Any four points in a plane, of which three are non-collinear are joined in order results into a four-sided closed figure called ‘quadrilateral’
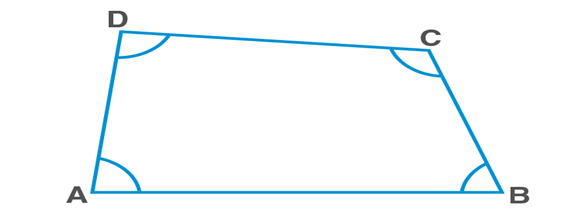
Quadrilateral
Angle sum property of a quadrilateral
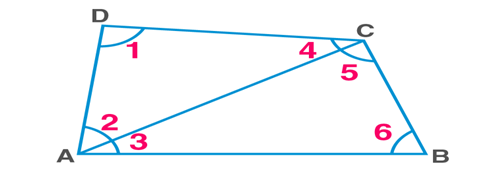
Angle sum property – Sum of angles in a quadrilateral is 360
In △ADC,
∠1+∠2+∠4=180 (Angle sum property of triangle)…………….(1)
In △ABC,
∠3+∠5+∠6=180 (Angle sum property of triangle)………………(2)
(1) + (2):
∠1+∠2+∠3+∠4+∠5+∠6=360
I.e, ∠A+∠B+∠C+∠D=360
Hence proved
Types of Quadrilaterals
Trapezium
A trapezium is a quadrilateral with any one pair of opposite sides parallel.

Trapezium
PQRS is a trapezium in which PQ||RS
Parallelogram
A parallelogram is a quadrilateral, with both pair of opposite sides parallel and equal. In a parallelogram, diagonals bisect each other.
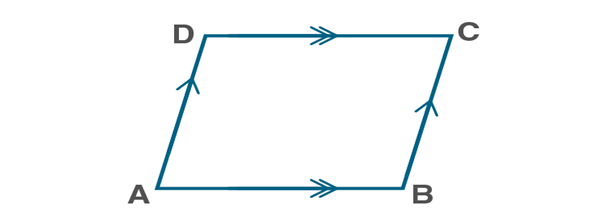
Parallelogram ABCD
Parallelogram ABCD in which AB||CD,BC||AD and AB=CD,BC=AD
Rhombus
A rhombus is a parallelogram with all sides equal. In a rhombus, diagonals bisect each other perpendicularly

Rhombus ABCD
A rhombus ABCD in which AB=BC=CD=AD and AC⊥BD
Rectangle
A rectangle is a parallelogram with all angles as right angles.

Rectangle ABCD
A rectangle ABCD in which, ∠A=∠B=∠C=∠D=900
Square
A square is a special case of a parallelogram with all angles as right angles and all sides equal.
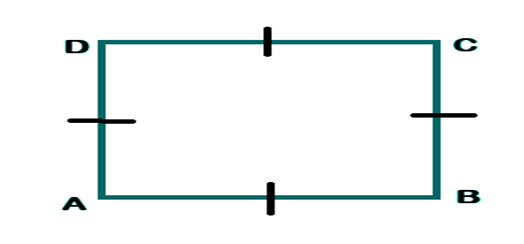
Square ABCD
Asquare ABCD in which ∠A=∠B=∠C=∠D=900 and AB=BC=CD=AD
Kite
A kite is a quadrilateral with adjacent sides equal.

Kite ABCD
A kite ABCD in which AB=BC and AD=CD
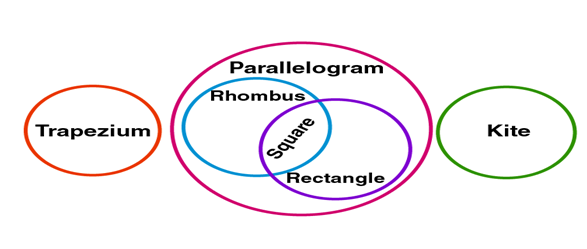
Venn diagram for different types of quadrilaterals