Exercise 2.4 Page: 43

1. Determine which of the following polynomials has (x + 1) a factor:

(i) x³+x²+x+1

Solution:

Let p(x) = x³+x²+x+1

The zero of x+1 is -1. [x+1 = 0 means x = -1]

p(−1) = (−1)³+(−1)²+(−1)+1

= −1+1−1+1

= 0

∴By factor theorem, x+1 is a factor of x³+x²+x+1

(ii) x⁴+x³+x²+x+1

Solution:

Let p(x)= x⁴+x³+x²+x+1

The zero of x+1 is -1. . [x+1= 0 means x = -1]

p(−1) = (−1)⁴+(−1)³+(−1)²+(−1)+1

= 1−1+1−1+1

= 1 ≠ 0

∴By factor theorem, x+1 is not a factor of x⁴ + x³ + x² + x + 1

(iii) x⁴+3x³+3x²+x+1 

Solution:

Let p(x)= x⁴+3x³+3x²+x+1

The zero of x+1 is -1.

p(−1)=(−1)4+3(−1)3+3(−1)2+(−1)+1

=1−3+3−1+1

=1 ≠ 0

∴By factor theorem, x+1 is not a factor of x⁴+3x³+3x²+x+1

(iv) x³ – x²– (2+√2)x +√2

Solution:

Let p(x) = x³–x²–(2+√2)x +√2

The zero of x+1 is -1.

p(−1) = (-1)³–(-1)²–(2+√2)(-1) + √2 = −1−1+2+√2+√2

= 2√2 ≠ 0

∴By factor theorem, x+1 is not a factor of x³–x²–(2+√2)x +√2

2. Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:

(i) p(x) = 2x³+x²–2x–1, g(x) = x+1

Solution:

p(x) = 2x³+x²–2x–1, g(x) = x+1

g(x) = 0

⇒ x+1 = 0

⇒ x = −1

∴Zero of g(x) is -1.

Now,

p(−1) = 2(−1)³+(−1)²–2(−1)–1

= −2+1+2−1

= 0

∴By factor theorem, g(x) is a factor of p(x).

(ii) p(x)=x³+3x²+3x+1, g(x) = x+2

Solution:

p(x) = x³+3x²+3x+1, g(x) = x+2

g(x) = 0

⇒ x+2 = 0

⇒ x = −2

∴ Zero of g(x) is -2.

Now,

p(−2) = (−2)³+3(−2)²+3(−2)+1

= −8+12−6+1

= −1 ≠ 0

∴By factor theorem, g(x) is not a factor of p(x).

(iii) p(x)=x³–4x²+x+6, g(x) = x–3

Solution:

p(x) = x³–4x²+x+6, g(x) = x -3

g(x) = 0

⇒ x−3 = 0

⇒ x = 3

∴ Zero of g(x) is 3.

Now,

p(3) = (3)³−4(3)²+(3)+6

= 27−36+3+6

= 0

∴By factor theorem, g(x) is a factor of p(x).

3. Find the value of k, if x–1 is a factor of p(x) in each of the following cases:

(i) p(x) = x²+x+k

Solution:

If x-1 is a factor of p(x), then p(1) = 0

By Factor Theorem

⇒ (1)²+(1)+k = 0

⇒ 1+1+k = 0

⇒ 2+k = 0

⇒ k = −2

(ii) p(x) = 2x²+kx+√2

Solution:

If x-1 is a factor of p(x), then p(1)=0

⇒ 2(1)²+k(1)+√2 = 0

⇒ 2+k+√2 = 0

⇒ k = −(2+√2)

(iii) p(x) = kx²–√2x+1

Solution:

If x-1 is a factor of p(x), then p(1)=0

By Factor Theorem

⇒ k(1)²-√2(1)+1=0

⇒ k = √2-1

(iv) p(x)=kx²–3x+k

Solution:

If x-1 is a factor of p(x), then p(1) = 0

By Factor Theorem

⇒ k(1)²–3(1)+k = 0

⇒ k−3+k = 0

⇒ 2k−3 = 0

⇒ k= 3/2

4. Factorize:

(i) 12x²–7x+1

Solution:

Using the splitting the middle term method,

We have to find a number whose sum = -7 and product =1×12 = 12

We get -3 and -4 as the numbers [-3+-4=-7 and -3×-4 = 12]

12x²–7x+1= 12x²-4x-3x+1

= 4x(3x-1)-1(3x-1)

= (4x-1)(3x-1)

(ii) 2x²+7x+3

Solution:

Using the splitting the middle term method,

We have to find a number whose sum = 7 and product = 2×3 = 6

We get 6 and 1 as the numbers [6+1 = 7 and 6×1 = 6]

2x²+7x+3 = 2x²+6x+1x+3

= 2x (x+3)+1(x+3)

= (2x+1)(x+3)

(iii) 6x²+5x-6 

Solution:

Using the splitting the middle term method,

We have to find a number whose sum = 5 and product = 6×-6 = -36

We get -4 and 9 as the numbers [-4+9 = 5 and -4×9 = -36]

6x²+5x-6 = 6x²+9x–4x–6

= 3x(2x+3)–2(2x+3)

= (2x+3)(3x–2)

(iv) 3x²–x–4 

Solution:

Using the splitting the middle term method,

We have to find a number whose sum = -1 and product = 3×-4 = -12

We get -4 and 3 as the numbers [-4+3 = -1 and -4×3 = -12]

3x²–x–4 = 3x²–x–4

= 3x²–4x+3x–4

= x(3x–4)+1(3x–4)

= (3x–4)(x+1)

5. Factorize:

(i) x³–2x²–x+2

Solution:

Let p(x) = x³–2x²–x+2

Factors of 2 are ±1 and ± 2

By trial method, we find that

p(1) = 0

So, (x+1) is factor of p(x)

Now,

p(x) = x³–2x²–x+2

p(−1) = (−1)³–2(−1)²–(−1)+2

= −1−1+1+2

= 0

Therefore, (x+1) is the factor of p(x)

Now, Dividend = Divisor × Quotient + Remainder

(x+1)(x²–3x+2) = (x+1)(x²–x–2x+2)

= (x+1)(x(x−1)−2(x−1))

= (x+1)(x−1)(x+2)

(ii) x³–3x²–9x–5

Solution:

Let p(x) = x³–3x²–9x–5

Factors of 5 are ±1 and ±5

By trial method, we find that

p(5) = 0

So, (x-5) is factor of p(x)

Now,

p(x) = x³–3x²–9x–5

p(5) = (5)³–3(5)²–9(5)–5

= 125−75−45−5

= 0

Therefore, (x-5) is the factor of  p(x)

Now, Dividend = Divisor × Quotient + Remainder

(x−5)(x²+2x+1) = (x−5)(x²+x+x+1)

= (x−5)(x(x+1)+1(x+1))

= (x−5)(x+1)(x+1)

(iii) x³+13x²+32x+20

Solution:

Let p(x) = x³+13x²+32x+20

Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20

By trial method, we find that

p(-1) = 0

So, (x+1) is factor of p(x)

Now,

p(x)= x³+13x²+32x+20

p(-1) = (−1)³+13(−1)²+32(−1)+20

= −1+13−32+20

= 0

Therefore, (x+1) is the factor of p(x)

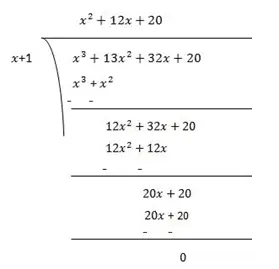
Now, Dividend = Divisor × Quotient +Remainder

(x+1)(x²+12x+20) = (x+1)(x²+2x+10x+20)

= (x−5)x(x+2)+10(x+2)

= (x−5)(x+2)(x+10)

(iv) 2y³+y²–2y–1

Solution:

Let p(y) = 2y³+y²–2y–1

Factors = 2×(−1)= -2 are ±1 and ±2

By trial method, we find that

p(1) = 0

So, (y-1) is factor of p(y)

Now,

p(y) = 2y³+y²–2y–1

p(1) = 2(1)³+(1)²–2(1)–1

= 2+1−2

= 0

Therefore, (y-1) is the factor of p(y)

Now, Dividend = Divisor × Quotient + Remainder

(y−1)(2y²+3y+1) = (y−1)(2y²+2y+y+1)

= (y−1)(2y(y+1)+1(y+1))

= (y−1)(2y+1)(y+1)

Class 9th Maths Polynomial