Exercise 13.7 Page No: 233
1. Find the volume of the right circular cone with
(i) radius 6cm, height 7 cm (ii) radius 3.5 cm, height 12 cm (Assume π = 22/7)
Solution:
Volume of cone = (1/3) πr2h cube units
Where r be radius and h be the height of the cone
(i) Radius of cone, r = 6 cm
Height of cone, h = 7cm
Say, V be the volume of the cone, we have
V = (1/3)×(22/7)×36×7
= (12×22)
= 264
The volume of the cone is 264 cm3.
(ii) Radius of cone, r = 3.5cm
Height of cone, h = 12cm
Volume of cone = (1/3)×(22/7)×3.52×7 = 154
Hence,
The volume of the cone is 154 cm3.
2. Find the capacity in litres of a conical vessel with
(i) radius 7cm, slant height 25 cm (ii) height 12 cm, slant height 12 cm
(Assume π = 22/7)
Solution:
(i) Radius of cone, r =7 cm
Slant height of cone, l = 25 cm
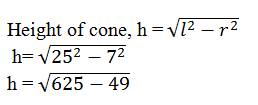
or h = 24
Height of the cone is 24 cm
Now,
Volume of cone, V = (1/3) πr2h (formula)
V = (1/3)×(22/7) ×72×24)
= (154×8)
= 1232
So, the volume of the vessel is 1232 cm3
Therefore, capacity of the conical vessel = (1232/1000) liters (because 1L = 1000 cm3)
= 1.232 Liters.
(ii) Height of cone, h = 12 cm
Slant height of cone, l = 13 cm

r = 5
Hence, the radius of cone is 5 cm.
Now, Volume of cone, V = (1/3)πr2h
V = (1/3)×(22/7)×52×12 cm3
= 2200/7
Volume of cone is 2200/7 cm3
Now, Capacity of the conical vessel= 2200/7000 litres (1L = 1000 cm3)
= 11/35 litres
3. The height of a cone is 15cm. If its volume is 1570cm3, find the diameter of its base. (Use π = 3.14)
Solution:
Height of the cone, h = 15 cm
Volume of cone =1570 cm3
Let r be the radius of the cone
As we know: Volume of cone, V = (1/3) πr2h
So, (1/3) πr2h = 1570
(1/3)×3.14×r2 ×15 = 1570
r2 = 100
r = 10
Radius of the base of cone 10 cm.
4. If the volume of a right circular cone of height 9cm is 48πcm3, find the diameter of its base.
Solution:
Height of cone, h = 9cm
Volume of cone =48π cm3
Let r be the radius of the cone.
As we know: Volume of cone, V = (1/3) πr2h
So, 1/3 π r2(9) = 48 π
r2 = 16
r = 4
Radius of cone is 4 cm.
So, diameter = 2×Radius = 8
Thus, diameter of base is 8cm.
5. A conical pit of top diameter 3.5m is 12m deep. What is its capacity in kiloliters?
(Assume π = 22/7)
Solution:
Diameter of conical pit = 3.5 m
Radius of conical pit, r = diameter/ 2 = (3.5/2)m = 1.75m
Height of pit, h = Depth of pit = 12m
Volume of cone, V = (1/3) πr2h
V = (1/3)×(22/7) ×(1.75)2×12 = 38.5
Volume of cone is 38.5 m3
Hence, capacity of the pit = (38.5×1) kiloliters = 38.5 kiloliters.
6. The volume of a right circular cone is 9856cm3. If the diameter of the base is 28cm, find
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone
(Assume π = 22/7)
Solution:
Volume of a right circular cone = 9856 cm3
Diameter of the base = 28 cm
(i) Radius of cone, r = (28/2) cm = 14 cm
Let the height of the cone be h
Volume of cone, V = (1/3) πr2h
(1/3) πr2h = 9856
(1/3)×(22/7) ×14×14×h = 9856
h = 48
The height of the cone is 48 cm.

Slant height of the cone is 50 cm.
(iii) curved surface area of cone = πrl
= (22/7)×14×50
= 2200
curved surface area of the cone is 2200 cm2.
7. A right triangle ABC with sides 5cm, 12cm and 13cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Solution:
Height (h)= 12 cm
Radius (r) = 5 cm, and
Slant height (l) = 13 cm
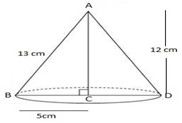
Volume of cone, V = (1/3) πr2h
V = (1/3)×π×52×12)
= 100π
Volume of the cone so formed is 100π cm3.
8. If the triangle ABC in the Question 7 is revolved about the side 5cm, then find the volume of the solids so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Solution:

A right-angled ΔABC is revolved about its side 5cm, a cone will be formed of radius as 12 cm, height as 5 cm, and slant height as 13 cm.
Volume of cone = (1/3) πr2h; where r is the radius and h be the height of cone
= (1/3)×π×12×12×5
= 240 π
The volume of the cones of formed is 240π cm3.
So, required ratio = (result of question 7) / (result of question 8) = (100π)/(240π) = 5/12 = 5:12.
9. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas.
(Assume π = 22/7)
Solution:
Radius (r) of heap = (10.5/2) m = 5.25
Height (h) of heap = 3m
Volume of heap = (1/3)πr2h
= (1/3)×(22/7)×5.25×5.25×3
= 86.625
The volume of the heap of wheat is 86.625 m3.
Again,

= (22/7)×5.25×6.05
= 99.825
Therefore, the area of the canvas is 99.825 m2.