Exercise 3.2 Page: 60

1. Write the answer of each of the following questions:

(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?

(ii) What is the name of each part of the plane formed by these two lines?

(iii) Write the name of the point where these two lines intersect.

Solution:

(i) The name of horizontal and vertical lines drawn to determine the position of any point in the Cartesian plane is x-axis and y-axis respectively.

(ii) The name of each part of the plane formed by these two lines x-axis and y-axis is quadrants.

(iii) The point where these two lines intersect is called the origin.

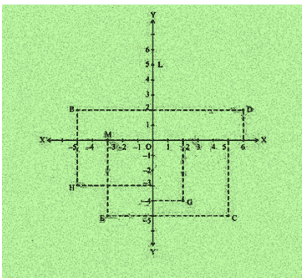
2. See Fig.3.14, and write the following:

i. The coordinates of B.

ii. The coordinates of C.

iii. The point identified by the coordinates (–3, –5).

iv. The point identified by the coordinates (2, – 4).

v. The abscissa of the point D.

vi. The ordinate of the point H.

vii. The coordinates of the point L.

viii. The coordinates of the point M.

Solution:

i. The co-ordinates of B is (−5, 2).

ii. The co-ordinates of C is (5, −5).

iii. The point identified by the coordinates (−3, −5) is E.

iv. The point identified by the coordinates (2, −4) is G.

v. Abscissa means x co-ordinate of point D. So, abscissa of the point D is 6.

vi. Ordinate means y coordinate of point H. So, ordinate of point H is -3.

vii. The co-ordinates of the point L is (0, 5).

viii. The co-ordinates of the point M is (−3, 0).

Exercise 3.3 Page: 651. In which quadrant or on which axis do each of the points (– 2, 4), (3, – 1), (– 1, 0), (1, 2) and (– 3, – 5) lie? Verify your answer by locating them on the Cartesian plane.

• (– 2, 4): Second Quadrant (II-Quadrant)
• (3, – 1): Fourth Quadrant (IV-Quadrant)
• (– 1, 0): Negative x-axis
• (1, 2): First Quadrant (I-Quadrant)
• (– 3, – 5): Third Quadrant (III-Quadrant)

2. Plot the points (x, y) given in the following table on the plane, choosing suitable units of distance on the axes.

Solution:

The points to plotted on the (x, y) are:

i. (-2, 8)

ii. (-1, 7)

iii. (0, -1.25)

iv. (1, 3)

v. (3, -1)

On the graph mark X-axis and Y-axis. Mark the meeting point as O.

Now, Let 1 unit = 1 cm

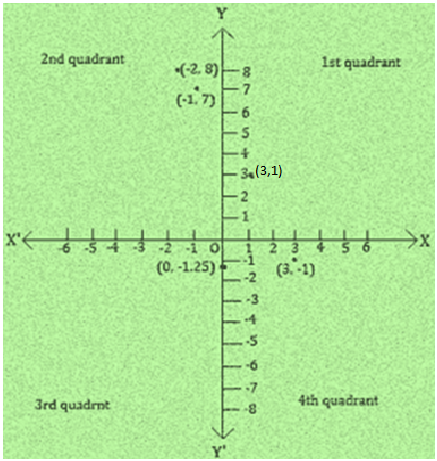
i. (-2, 8): II- Quadrant, Meeting point of the imaginary lines that starts from 2 units to the left of origin O and from 8 units above the origin O

ii. (-1, 7): II- Quadrant, Meeting point of the imaginary lines that starts from 1 units to the left of origin O and from 7 units above the origin O

iii. (0, -1.25): On the x-axis, 1.25 units to the left of origin O

iv. (1, 3): I- Quadrant, Meeting point of the imaginary lines that starts from 1 units to the right of origin O and from 3 units above the origin O

v. (3, -1): IV- Quadrant, Meeting point of the imaginary lines that starts from 3 units to the right of origin O and from 1 units below the origin O