Exercise: 7.3 (Page No: 128)
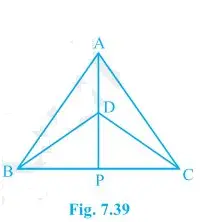
1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) ΔABD ΔACD
(ii) ΔABP ΔACP
(iii) AP bisects A as well as D.
(iv) AP is the perpendicular bisector of BC.
Solution:
In the above question, it is given that ΔABC and ΔDBC are two isosceles triangles.
(i) ΔABD and ΔACD are similar by SSS congruency because:
AD = AD (It is the common arm)
AB = AC (Since ΔABC is isosceles)
BD = CD (Since ΔDBC is isosceles)
∴ ΔABD ΔACD.
(ii) ΔABP and ΔACP are similar as:
AP = AP (It is the common side)
PAB = PAC (by CPCT since ΔABD ΔACD)
AB = AC (Since ΔABC is isosceles)
So, ΔABP ΔACP by SAS congruency condition.
(iii) PAB = PAC by CPCT as ΔABD ΔACD.
AP bisects A. — (i)
Also, ΔBPD and ΔCPD are similar by SSS congruency as
PD = PD (It is the common side)
BD = CD (Since ΔDBC is isosceles.)
BP = CP (by CPCT as ΔABP ΔACP)
So, ΔBPD ΔCPD.
Thus, BDP = CDP by CPCT. — (ii)
Now by comparing (i) and (ii) it can be said that AP bisects A as well as D.
(iv) BPD = CPD (by CPCT as ΔBPD ΔCPD)
and BP = CP — (i)
also,
BPD +CPD = 180° (Since BC is a straight line.)
⇒ 2BPD = 180°
⇒ BPD = 90° —(ii)
Now, from equations (i) and (ii), it can be said that
AP is the perpendicular bisector of BC.
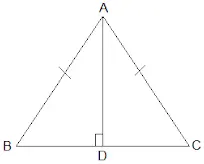
2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects A.
Solution: It is given that AD is an altitude and AB = AC. The diagram is as follows:
(i) In ΔABD and ΔACD,
ADB = ADC = 90°
AB = AC (It is given in the question)
AD = AD (Common arm)
∴ ΔABD ΔACD by RHS congruence condition.
Now, by the rule of CPCT,
BD = CD.
So, AD bisects BC
(ii) Again, by the rule of CPCT, BAD = CAD
Hence, AD bisects A.
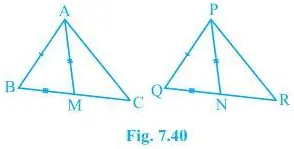
3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:
(i) ΔABM ΔPQN
(ii) ΔABC ΔPQR
Solution:
Given parameters are:
AB = PQ,
BC = QR and
AM = PN
(i) ½ BC = BM and ½ QR = QN (Since AM and PN are medians)
Also, BC = QR
So, ½ BC = ½ QR
⇒ BM = QN
In ΔABM and ΔPQN,
AM = PN and AB = PQ (As given in the question)
BM = QN (Already proved)
∴ ΔABM ΔPQN by SSS congruency.
(ii) In ΔABC and ΔPQR,
AB = PQ and BC = QR (As given in the question)
ABC = PQR (by CPCT)
So, ΔABC ΔPQR by SAS congruency.
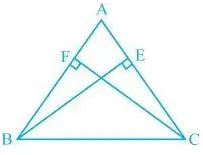
4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Solution:
It is known that BE and CF are two equal altitudes.
Now, in ΔBEC and ΔCFB,
BEC = CFB = 90° (Same Altitudes)
BC = CB (Common side)
BE = CF (Common side)
So, ΔBEC ΔCFB by RHS congruence criterion.
Also, C = B (by CPCT)
Therefore, AB = AC as sides opposite to the equal angles is always equal.
5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that B = C.
Solution:
In the question, it is given that AB = AC
Now, ΔABP and ΔACP are similar by RHS congruency as
APB = APC = 90° (AP is altitude)
AB = AC (Given in the question)
AP = AP (Common side)
So, ΔABP ΔACP.
∴ B = C (by CPCT)