Exercise 1.3 Page: 14

1. Write the following in decimal form and say what kind of decimal expansion each has :

(i) 36/100

Solution:

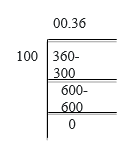
= 0.36 (Terminating)

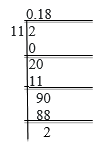
(ii)1/11

Solution:

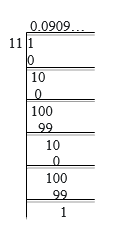
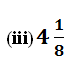
Solution:

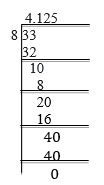
= 4.125 (Terminating)

(iv) 3/13

Solution:

(v) 2/11

Solution:

(vi) 329/400 Solution:

= 0.8225 (Terminating)

2. You know that 1/7 = 0.142857. Can you predict what the decimal expansions of 2/7, 3/7, 4/7, 5/7, 6/7 are, without actually doing the long division? If so, how?

[Hint: Study the remainders while finding the value of 1/7 carefully.]

Solution:

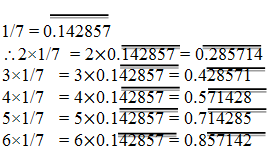
3. Express the following in the form p/q, where p and q are integers and q 0.

(i) 

Solution:

Assume that  x = 0.666…

Then,10x = 6.666…

10x = 6 + x

9x = 6

x = 2/3

(ii) 0.4\overline{7}0.47

Solution:

0.4\overline{7} = 0.4777..0.47=0.4777..

= (4/10)+(0.777/10)

Assume that x = 0.777…

Then, 10x = 7.777…

10x = 7 + x

x = 7/9

(4/10)+(0.777../10) = (4/10)+(7/90) ( x = 7/9 and x = 0.777…0.777…/10 = 7/(9×10) = 7/90 ) = (36/90)+(7/90) = 43/90

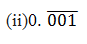
Solution:

Assume that  x = 0.001001…

Then, 1000x = 1.001001…

1000x = 1 + x

999x = 1

x = 1/999

4. Express 0.99999…. in the form p/q . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.

Solution:

Assume that x = 0.9999…..Eq (a)

Multiplying both sides by 10,

10x = 9.9999…. Eq. (b)

Eq.(b) – Eq.(a), we get

(10x = 9.9999)-(x = 0.9999…)

9x = 9

x = 1

The difference between 1 and 0.999999 is 0.000001 which is negligible.

Hence, we can conclude that, 0.999 is too much near 1, therefore, 1 as the answer can be justified.

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17 ? Perform the division to check your answer.

Solution:

1/17

Dividing 1 by 17:

There are 16 digits in the repeating block of the decimal expansion of 1/17.

6. Look at several examples of rational numbers in the form p/q (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?

Solution:

We observe that when q is 2, 4, 5, 8, 10… Then the decimal expansion is terminating. For example:

1/2 = 0. 5, denominator q = 2¹

7/8 = 0. 875, denominator q =2³

4/5 = 0. 8, denominator q = 5¹

We can observe that the terminating decimal may be obtained in the situation where prime factorization of the denominator of the given fractions has the power of only 2 or only 5 or both.

7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Solution:

We know that all irrational numbers are non-terminating non-recurring. three numbers with decimal expansions that are non-terminating non-recurring are:

1. √3 = 1.732050807568
2. √26 =5.099019513592
3. √101 = 10.04987562112

8. Find three different irrational numbers between the rational numbers 5/7 and 9/11.

Solution:

hree different irrational numbers are:

1. 0.73073007300073000073…
2. 0.75075007300075000075…
3. 0.76076007600076000076…

9.  Classify the following numbers as rational or irrational according to their type:

(i)√23

Solution:

√23 = 4.79583152331…

Since the number is non-terminating non-recurring therefore, it is an irrational number.

(ii)√225

Solution:

√225 = 15 = 15/1

Since the number can be represented in p/q form, it is a rational number.

(iii) 0.3796

Solution:

Since the number,0.3796, is terminating, it is a rational number.

(iv) 7.478478

Solution:

The number,7.478478, is non-terminating but recurring, it is a rational number.

(v) 1.101001000100001…

Solution:

Since the number,1.101001000100001…, is non-terminating non-repeating (non-recurring), it is an irrational number.