Exercise 1.5 Page: 24

1. Classify the following numbers as rational or irrational:

(i) 2 –√5

Solution:

We know that, √5 = 2.2360679…

Here, 2.2360679…is non-terminating and non-recurring.

Now, substituting the value of √5 in 2 –√5, we get,

2-√5 = 2-2.2360679… = -0.2360679

Since the number, – 0.2360679…, is non-terminating non-recurring, 2 –√5 is an irrational number.

(ii) (3 +√23)- √23

Solution:

(3 +√23) –√23 = 3+√23–√23

= 3

= 3/1

Since the number 3/1 is in p/q form, (3 +√23)- √23 is rational.

(iii) 2√7/7√7

Solution:

2√7/7√7 = ( 2/7)× (√7/√7)

We know that (√7/√7) = 1

Hence, ( 2/7)× (√7/√7) = (2/7)×1 = 2/7

Since the number, 2/7 is in p/q form, 2√7/7√7 is rational.

(iv) 1/√2

Solution:

Multiplying and dividing numerator and denominator by √2 we get,

(1/√2) ×(√2/√2)= √2/2 ( since √2×√2 = 2)

We know that, √2 = 1.4142…

Then, √2/2 = 1.4142/2 = 0.7071..

Since the number , 0.7071..is non-terminating non-recurring, 1/√2 is an irrational number.

(v) 2

Solution:

We know that, the value of = 3.1415

Hence, 2 = 2×3.1415.. = 6.2830…

Since the number, 6.2830…, is non-terminating non-recurring, 2 is an irrational number.

2. Simplify each of the following expressions:

(i) (3+√3)(2+√2)

Solution:

(3+√3)(2+√2 )

Opening the brackets, we get, (3×2)+(3×√2)+(√3×2)+(√3×√2)

= 6+3√2+2√3+√6

(ii) (3+√3)(2+√2 )

Solution:

(3+√3)(2+√2 ) = 3²-(√3)² = 9-3

= 6

(iii) (√5+√2)²

Solution:

(√5+√2)² = √5²+(2×√5×√2)+ √2²

= 5+2×√10+2 = 7+2√10

(iv) (√5-√2)(√5+√2)

Solution:

(√5-√2)(√5+√2) = (√5²-√2²) = 5-2 = 3

3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter, (say d). That is, π =c/d. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

Solution:

There is no contradiction. When we measure a value with a scale, we only obtain an approximate value. We never obtain an exact value. Therefore, we may not realize whether c or d is irrational. The value of π is almost equal to 22/7 or 3.142857…

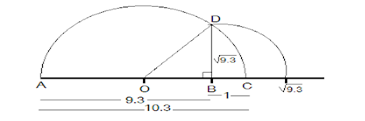
4. Represent (√9.3) on the number line.

Solution:

Step 1: Draw a 9.3 units long line segment, AB. Extend AB to C such that BC=1 unit.

Step 2: Now, AC = 10.3 units. Let the centre of AC be O.

Step 3: Draw a semi-circle of radius OC with centre O.

Step 4: Draw a BD perpendicular to AC at point B intersecting the semicircle at D. Join OD.

Step 5: OBD, obtained, is a right angled triangle.

Here, OD 10.3/2 (radius of semi-circle), OC = 10.3/2 , BC = 1

OB = OC – BC

⟹ (10.3/2)-1 = 8.3/2

Using Pythagoras theorem,

We get,

OD²=BD²+OB²

⟹ (10.3/2)² = BD²+(8.3/2)²

⟹ BD^{2 =} (10.3/2)²-(8.3/2)²

⟹ (BD)² = (10.3/2)-(8.3/2)(10.3/2)+(8.3/2)

⟹ BD² = 9.3

⟹ BD =  √9.3

Thus, the length of BD is √9.3.

Step 6: Taking BD as radius and B as centre draw an arc which touches the line segment. The point where it touches the line segment is at a distance of √9.3 from O as shown in the figure.

5. Rationalize the denominators of the following:

(i) 1/√7

Solution:

Multiply and divide 1/√7 by √7

(1×√7)/(√7×√7) = √7/7

(ii) 1/(√7-√6)

Solution:

Multiply and divide 1/(√7-√6) by (√7+√6)

[1/(√7-√6)]×(√7+√6)/(√7+√6) = (√7+√6)/(√7-√6)(√7+√6)

= (√7+√6)/√7²-√6² [denominator is obtained by the property, (a+b)(a-b) = a²-b²]

= (√7+√6)/(7-6)

= (√7+√6)/1

= √7+√6

(iii) 1/(√5+√2)

Solution:

Multiply and divide 1/(√5+√2) by (√5-√2)

[1/(√5+√2)]×(√5-√2)/(√5-√2) = (√5-√2)/(√5+√2)(√5-√2)

= (√5-√2)/(√5²-√2²) [denominator is obtained by the property, (a+b)(a-b) = a²-b²]

= (√5-√2)/(5-2)

= (√5-√2)/3

(iv) 1/(√7-2)

Solution:

Multiply and divide 1/(√7-2) by (√7+2)

1/(√7-2)×(√7+2)/(√7+2) = (√7+2)/(√7-2)(√7+2)

= (√7+2)/(√7²-2²) [denominator is obtained by the property, (a+b)(a-b) = a²-b²]

= (√7+2)/(7-4)

= (√7+2)/3